Co to jest integralna? Całki ze szczegółowym rozwiązaniem. Zintegrowana tabela
Słowo "integralna" pochodzi od łacińskiej integralis - holistycznej. Tytuł ten jest proponowany w XVII wieku. uczeń wielkiego Leibniza (a także wybitnego matematyka) I. Bernoulli. A jaka jest integralność w nowoczesnym sensie? Poniżej postaramy się udzielić wyczerpującej odpowiedzi na to pytanie.
Tło historyczne koncepcji całki
Na początku XVII wieku przy rozważaniu czołowych naukowców istniała duża liczba zadań fizycznych (głównie mechanicznych), w których konieczne było zbadanie zależności niektórych wielkości od innych. Najbardziej oczywistym i palącym problemem było określenie chwilowej prędkości nierównomiernego ruchu ciała w danym momencie i jego odwrotnego problemu znalezienia wielkości ścieżki przemieszczanej przez ciało w pewnym okresie czasu podczas takiego ruchu. Dziś już wiemy, jaka jest integralna część prędkości ruchu - jest to droga, którą przebył. Ale zrozumienie, jak to obliczyć, znając prędkość w każdej chwili, nie pojawiło się natychmiast.
Najpierw z rozważenia takich zależności wielkości fizycznych, na przykład od prędkości, ukształtowała się matematyczna koncepcja funkcji y = f (x). Badanie właściwości różnych funkcji doprowadziło do pojawienia się analiza matematyczna. Naukowcy aktywnie poszukują sposobów badania właściwości różnych funkcji. 
Jak obliczono całki i pochodne?
Po tym jak Descartes stworzył podstawy geometrii analitycznej i możliwość graficznego przedstawienia zależności funkcjonalnych w osiach kartezjańskiego układu współrzędnych, badacze musieli zmierzyć się z dwoma głównymi nowymi zadaniami: jak narysować styczną do zakrzywionej linii w dowolnym punkcie i jak znaleźć obszar figury ograniczonej powyżej tej krzywej i linii prostych, równolegle do osi współrzędnych. W nieoczekiwany sposób okazało się, że pierwszy jest równoznaczny ze znalezieniem chwilowej prędkości, a drugi z odległością przebytą. Wszakże w przypadku nierównomiernego ruchu, został on przedstawiony w kartezjańskich osiach współrzędnych "odległość" i "czas" z pewną zakrzywioną linią.
Genius Leibniz i Newton w połowie XVII wieku. stworzono metody, które pozwoliły rozwiązać oba problemy. Okazało się, że w celu przeprowadzenia stycznej do krzywej w punkcie, konieczne jest znalezienie wartości tzw. Pochodnej funkcji opisującej tę krzywą w danym punkcie, a ta wartość jest równa szybkości zmiany funkcji, tj. W odniesieniu do zależności "droga w stosunku do prędkości". natychmiastowa prędkość ciała.
Aby znaleźć obszar ograniczony krzywą, konieczne było obliczenie pewnej całki, która dała jej dokładną wartość. Pochodna i całka - podstawowe pojęcia rachunku różniczkowego i całkowego, które są podstawą współczesnej analizy matematycznej - najważniejszego działu matematyki wyższej.
Obszar pod krzywą
A więc, jak to zdefiniować dokładna wartość? Spróbujmy od samego początku odkryć proces jego obliczania poprzez szczegółową całkę.
Niech f będzie funkcją ciągłą w przedziale [ab]. Rozważmy krzywą y = f (x) pokazaną na poniższym rysunku. Jak znaleźć obszar obszaru ograniczony przez krzywą), oś X i linie x = a i x = b? To znaczy obszar zacienionej figury na rysunku. 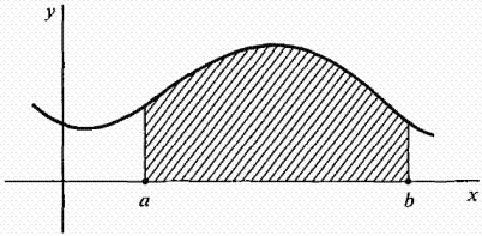
Najprostszym przypadkiem jest, gdy f jest stałą funkcją; to znaczy, krzywa jest linią poziomą f (X) = k, gdzie k jest stałą i k ≥ 0, jak pokazano na poniższym rysunku. 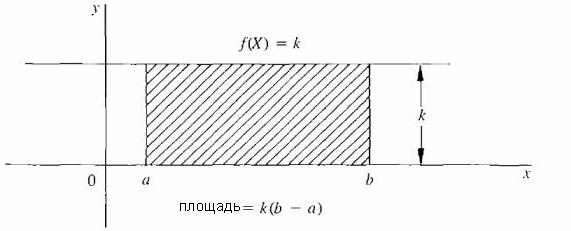 W tym przypadku obszar pod krzywą jest prostok¹tem o wysokoœci k i szerokoœci (b - a), dlatego obszar ten definiowany jest jako: k · (b - a).
W tym przypadku obszar pod krzywą jest prostok¹tem o wysokoœci k i szerokoœci (b - a), dlatego obszar ten definiowany jest jako: k · (b - a).
Obszary innych prostych kształtów, takich jak trójkąt, trapez i półkole, są określone przez wzory planimetryczne.
Obszar pod dowolną ciągłą krzywą y = f (x) jest określony całką określoną, która jest zapisana w taki sam sposób jak całka normalna.
Riemann suma
Zanim zajmiemy się szczegółową odpowiedzią na pytanie o to, czym jest integralna, podkreślimy kilka podstawowych idei.
Po pierwsze, obszar pod krzywą jest podzielony na pewną liczbę n pionowych pasków o wystarczająco małej szerokości Δx. Ponadto każdy pionowy pasek jest zastępowany pionowym prostokątem o wysokości f (x), szerokości Δx i obszarze f (x) dx. Następnym krokiem jest utworzenie sumy obszarów wszystkich tych prostokątów, zwanych sumą Riemannian (patrz rysunki poniżej).
Rysując nasze prostokąty Δx szerokie, możemy przyjąć ich wysokość równą wartości funkcji na lewej krawędzi każdego paska, tj. Krzywa będzie skrajnymi lewymi punktami ich górnych krótkich boków Δx. W tym samym czasie, w sekcji, w której funkcja rośnie, a jej krzywa jest wypukła, wszystkie prostokąty znajdują się poniżej tej krzywej, tj. Ich suma będzie z pewnością mniejsza niż dokładna wartość obszaru pod krzywą w tym obszarze (patrz rysunek poniżej). Ta metoda aproksymacji nazywana jest lewostronną. 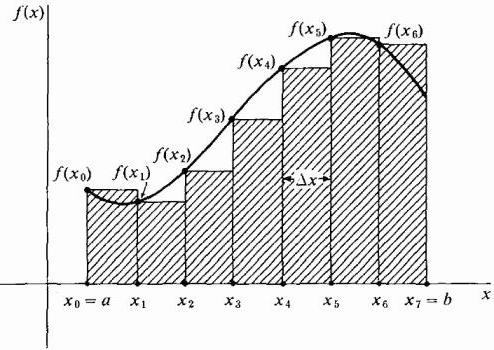
W zasadzie możliwe jest narysowanie przybliżających się prostokątów w taki sposób, że skrajne prawe punkty ich górnych krótkich boków o szerokości Δx leżą na krzywej. Wtedy będą wyższe od krzywej, a przybliżenie obszaru w tym obszarze będzie większe niż jego dokładna wartość, jak pokazano na poniższym rysunku. Ta metoda nazywa się prawem. 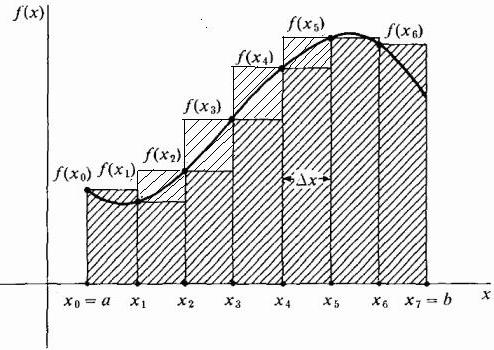
Ale możemy również przyjąć wysokość każdego przybliżającego prostokąta równą tylko pewnej wartości funkcji w dowolnym punkcie x * i wewnątrz odpowiedniego paska Δx i (patrz rys. poniżej). W takim przypadku nie możemy nawet przyjąć tej samej szerokości wszystkich pasków. 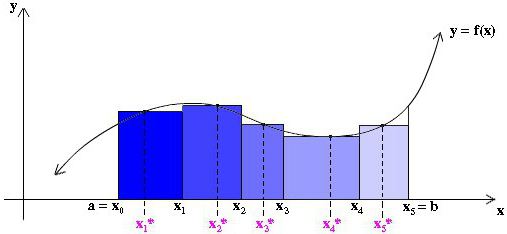
Tworzymy kwotę Riemann:

Przejście od sumy Riemanna do pewnej całki
W matematyce wyższej dowodzi się twierdzenia, które stwierdza, że jeśli przy nieograniczonym wzroście liczby n przybliżających się prostokątów ich największa szerokość dąży do zera, wówczas suma Riemanowa A n zmierza do pewnej granicy A. Liczba A jest taka sama dla każdej metody tworzenia przybliżających się prostokątów i dla dowolnego wyboru punktów x * i .
Wyjaśnione wyjaśnienie twierdzenia podano na poniższym rysunku.
Pokazuje to, że im węższe prostokąty, tym bliżej obszaru schodkowej figury do obszaru pod krzywą. Gdy liczba prostokątów n → ∞, ich szerokość wynosi Δx i → 0, a granica A sumy A n jest liczbowo równa wymaganemu obszarowi. Ten limit i jest pewna integralna część funkcji f (x): 
Symbol złożony, który jest zmodyfikowaną kursywą S, został wprowadzony przez Leibniza. J. B. Fourier zaproponował umieszczenie notacji całki u góry i u dołu. W tym samym czasie wyraźnie zaznaczono początkowe i końcowe wartości x.
Geometryczna i mechaniczna interpretacja całki oznaczonej
Spróbujmy udzielić szczegółowej odpowiedzi na pytanie, czym jest całka? Rozważ całkę na przedziale [a, b] z funkcji dodatniej f (x) w środku i przyjmij, że górny limit jest większy niż dolny Jeżeli rzędne funkcji f (x) są ujemne wewnątrz [a, b], to bezwzględna wartość całki jest równa powierzchni między osią x a wykresem y = f (x), sama integralna jest ujemna. W przypadku pojedynczego lub wielokrotnego przecięcia osi y = f (x) odciętej w segmencie [a, b], jak pokazano na poniższym rysunku, w celu obliczenia całki konieczne jest określenie różnicy, w której spadek jest równy całkowitemu obszarowi wykresów powyżej osi X i odliczeniu - całkowity obszar obszarów pod nim. Mechaniczna interpretacja określonej całki jest ściśle związana z geometrią. Powróćmy do sekcji "suma Riemanna" i wyobraźmy sobie, że wykres pokazany na rysunkach wyraża funkcję prędkości v = f (t) z nierównomiernym ruchem punkt materialny (oś odciętych jest osią czasu). Następnie obszar dowolnego przybliżonego prostokąta o szerokości Δt, który zbudowaliśmy podczas tworzenia sumy Riemanna, będzie wyrażał w przybliżeniu ścieżkę punktu w czasie Δt, mianowicie v (t *) Δt. Całkowita suma obszarów prostokątów w przedziale od t 1 = a do t 2 = b wyraża w przybliżeniu ścieżkę s w czasie t 2 - t 1 , a jego granica, czyli całka (zdefiniowana) od a do b funkcji v = f (t) przez dt, poda dokładną wartość ścieżki s. Jeśli powrócimy do jego oznaczenia, możemy przyjąć, że a = const, i b jest określoną wartością pewnej niezależnej zmiennej x. Następnie określona całka z górną granicą x z konkretnej liczby zamienia się w funkcję x. Taka całka jest równa powierzchni figury pod krzywą wskazaną przez punkty aABb na poniższym rysunku. Załóżmy, że zmienną x = b nadaliśmy niewielkiemu przyrostowi Δx. Następnie przyrost powierzchni figury aABb składa się z obszaru prostokąta (zacienionego na rysunku) Bb ∙ Δx i obszaru figury BDC pod krzywą. Obszar prostokąta jest równy Bb ∙ Δx f = f (x) Δx, to znaczy jest liniową funkcją przyrostu zmiennej niezależnej. Obszar kształtu BDC jest oczywiście mniejszy niż obszar prostokąta BDCK = Δx ∙ Δy, a ponieważ Δx → 0 dąży, maleje nawet szybciej. Stąd, f (x) Δx = f (x) dx jest różnicą zmiennej powierzchni aABb, tj. Różnicą określonej całki Na tej podstawie możemy wywnioskować, że obliczanie całek polega na znalezieniu funkcji z określonych wyrażeń ich różnic. Rachunek całkowy to właśnie system metod wyszukiwania takich funkcji na podstawie ich znanych różnic. Łączy związek między różnicowaniem a integracją i pokazuje, że istnieje operacja odwrotna do różnicowania funkcji - jej integracji. Pokazuje także, że jeśli jakakolwiek funkcja f (x) jest ciągła, to przez zastosowanie tej operacji matematycznej można znaleźć cały zespół (zbiór, zestaw) funkcji prymitywnej dla niego (lub inaczej, znaleźć z niej nieskończoną całość). Niech funkcja F (x) będzie oznaczeniem wyniku integracji funkcji f (x). Powiązanie między tymi dwiema funkcjami w wyniku integracji drugiego z nich jest wskazane w następujący sposób: Jak widać, z integralnym symbolem nie ma ograniczeń integracji. Oznacza to, że z określonego przekształca się w nieskończoną całość. Słowo "nieokreślony" oznacza, że wynikiem operacji integracji w tym przypadku nie jest jedna, ale wiele funkcji. Rzeczywiście, poza samą funkcją F (x), każda funkcja F (x) + C spełnia ostatnie wyrażenia, gdzie C = const. Oznacza to, że stały członek zespołu asocjatywnych może być ustawiany arbitralnie. Należy podkreślić, że jeśli całka zdefiniowana przez funkcję jest liczbą, to nieskończoność jest funkcją, a ściślej mówiąc, ich zbiorem. Termin "integracja" służy do definiowania wyszukiwania dla obu typów całek. Jest całkowitym przeciwieństwem odpowiedniej reguły dla różnicowania. W jaki sposób są wykonywane całki nieoznaczone? Przykłady tej procedury, rozważamy konkretne funkcje. Spójrzmy na funkcję mocy w ogólnej formie: f (x) = cx n Po wykonaniu tego w każdym z terminów w wyrażeniu funkcji całkowalnej (jeśli jest ich kilka), dodajemy stałą na końcu. Przypomnij sobie, że pobranie pochodnej o wartości stałej niszczy ją, więc przyjęcie całki dowolnej funkcji da nam przywrócenie tej stałej. Oznaczamy go przez C, ponieważ stała jest nieznana - może to być dowolna liczba! Dlatego możemy mieć nieskończenie wiele wyrażeń dla całki nieoznaczonej. Rzućmy okiem na proste całki nieoznaczone, których przykłady pokazano poniżej. Załóżmy, że musisz znaleźć całkę funkcji: f (x) = 4x 2 + 2x - 3. Zacznijmy od pierwszego terminu. Patrzymy na wykładnik 2 i zwiększamy go o 1, następnie dzielimy pierwszy termin przez wynikowy wskaźnik 3. Otrzymujemy: 4 (x 3 ) / 3. Następnie patrzymy na następnego członka i robimy to samo. Ponieważ ma wykładnik 1, wynikowy wskaźnik będzie wynosił 2. Dlatego dzielimy ten termin przez 2: 2 (x 2 ) / 2 = x 2 . Ostatni termin ma współczynnik x, ale po prostu go nie widzimy. Możemy sobie wyobrazić ostatni termin jako (-3x 0 ). Jest to odpowiednik (-3) ∙ (1). Jeśli użyjemy reguły integracji, dodamy 1 do wskaźnika, aby podnieść go do pierwszego stopnia, a następnie dzielimy ostatni termin przez 1. Otrzymujemy 3x. Ta reguła integracji działa dla wszystkich wartości n, oprócz n = - 1 (ponieważ nie możemy dzielić przez 0). Rozważaliśmy najprostszy przykład znalezienia całki. Ogólnie rzecz biorąc, rozwiązanie całek nie jest łatwym zadaniem, a doświadczenie już zdobyte w matematyce jest w tym pomocne. W powyższej sekcji widzieliśmy, że z każdej formuły różnicowania uzyskuje się odpowiednią formułę całkowania. Dlatego wszystkie ich możliwe opcje zostały już dawno uzyskane i podsumowane w odpowiednich tabelach. Poniższa tabela całek zawiera formuły do integracji podstawowych funkcji algebraicznych. Te formuły należy zapamiętać, zapamiętywać je stopniowo, ponieważ są one ćwiczeniami stałymi. Inna tabela całek zawiera główne funkcje trygonometryczne: Okazuje się, że aby to zrobić, możliwość integracji, czyli znalezienie nieskończonych całek, jest bardzo prosta. Pomaga w tym formuła założycieli rachunku różniczkowego Newtona-Leibniza. Zgodnie z tym, na pierwszym etapie obliczenie pożądanej całki polega na znalezieniu nieokreślonego, a następnie obliczeniu wartości znalezionego prymitywu F (x) z podstawieniem x, równym najpierw górnej granicy, a następnie niższej, a na końcu wyznaczeniu różnicy tych wartości. W tym przypadku nie można zapisać stałej C. ponieważ znika podczas wykonywania odejmowania. Uważamy niektóre całki za szczegółowe rozwiązanie. Znajdź obszar witryny pod jedną falą sinusoidalną półfalową. Obecnie rozważamy całki za pomocą szczegółowego rozwiązania, które wykorzystuje właściwość addytywności w pierwszym przykładzie, oraz zastąpienie pośredniej zmiennej integracji w drugim przykładzie. Obliczamy całkę określoną o frakcyjnie racjonalnej funkcji: y = (1 + t) / t3 od t = 1 do t = 2. Teraz pokażemy, jak uprościć przyjmowanie całki przez wprowadzenie zmiennej pośredniej. Załóżmy, że musisz obliczyć całkę (x + 1) 2 . Mówiliśmy o pewnej całce dla skończonego przedziału [a, b] funkcji f (x) ciągłej na nim. Ale szereg specyficznych problemów prowadzi do potrzeby rozszerzenia koncepcji integralnej do przypadku, gdy granice (jedna lub obie) są równe nieskończoności lub gdy funkcja nieciągłości. Na przykład podczas obliczania obszarów pod krzywymi asymptotycznie zbliża się do osi współrzędnych. Aby rozszerzyć koncepcję całki do tego przypadku, oprócz przejścia do granicy, podczas obliczania sumy Riemanna przybliżających się prostokątów, wykonywana jest kolejna. Przy takim podwójnym przejściu do granicy uzyskuje się niewłaściwą całkę. W przeciwieństwie do tego wszystkie wymienione powyżej całki nazywane są właściwymi. 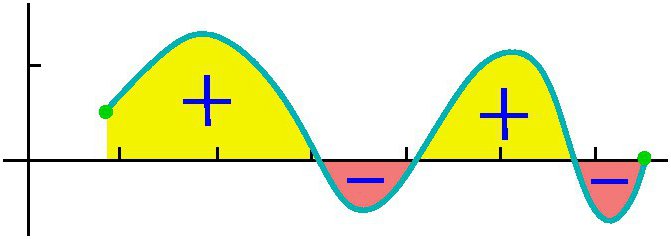 Tak więc, dla funkcji pokazanej na powyższym rysunku, całka oznaczona od a do b będzie (S1 + S3) - (S2 + S4).
Tak więc, dla funkcji pokazanej na powyższym rysunku, całka oznaczona od a do b będzie (S1 + S3) - (S2 + S4). Dyferencjał określonej całki
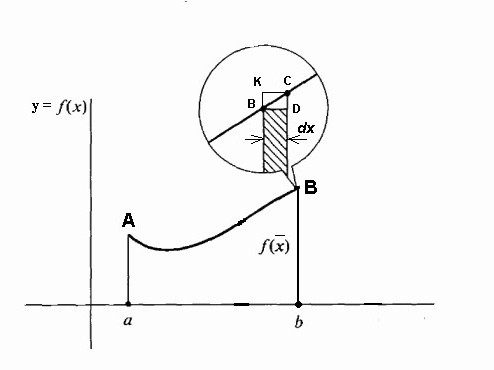 W przypadku linii stałej aA i ruchomej Bb obszar ten staje się funkcją f (x), przy czym przyrosty Δx nadal są osadzane wzdłuż osi x, a przyrosty funkcji f (x) oznaczają przyrosty powierzchni pod krzywą.
W przypadku linii stałej aA i ruchomej Bb obszar ten staje się funkcją f (x), przy czym przyrosty Δx nadal są osadzane wzdłuż osi x, a przyrosty funkcji f (x) oznaczają przyrosty powierzchni pod krzywą. 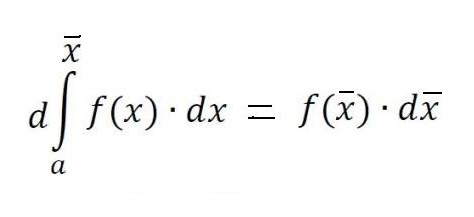
Podstawowy współczynnik rachunku całkowego
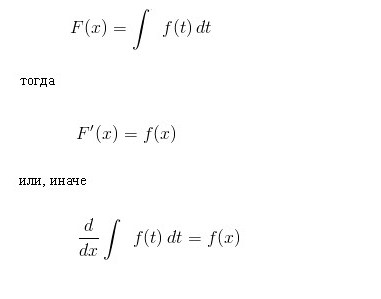
Podstawowa zasada integracji

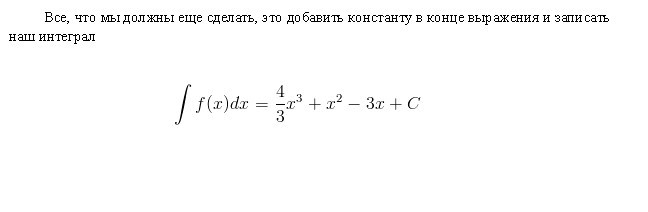

Zintegrowane tabele
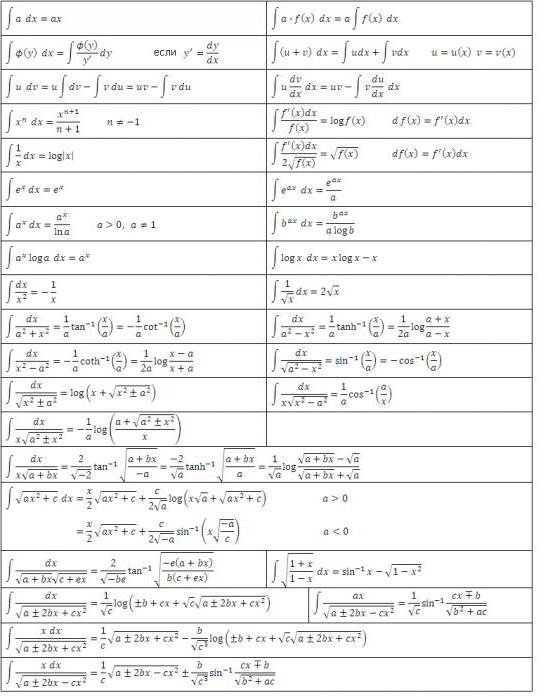

Jak obliczyć pewną całkę
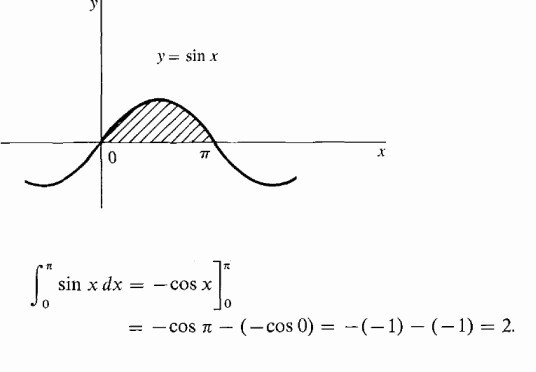 Oblicz zacieniony obszar pod hiperbolą.
Oblicz zacieniony obszar pod hiperbolą. 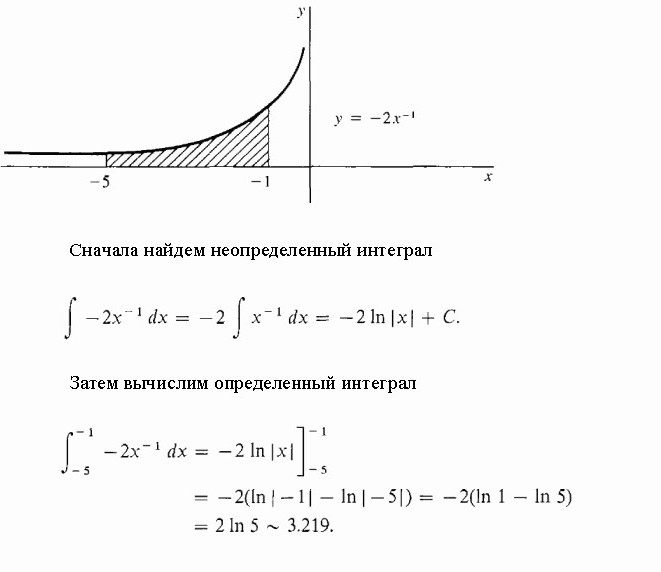
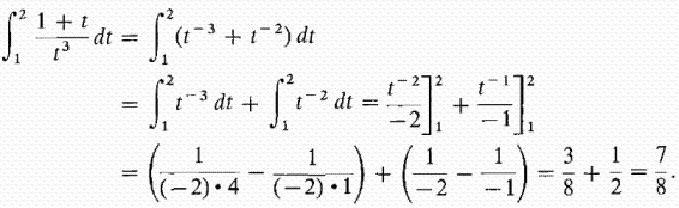
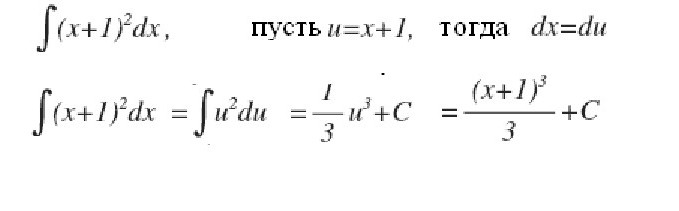
Informacje o nieprawidłowych całkach