Jaki jest moment bezwładności: wzory na wędkę i koło

Każdy ruch ciał w przestrzeni, którego trajektoria jest kołem, oznacza nie tylko znajomość prędkości kątowej, ale także moment bezwładności dla opisu tego ruchu. Jaki jest moment bezwładności, a także to, co jest równe dla drążka i koła, ten artykuł odpowie.

Obrót i moment bezwładności

Fizyczną wielkość, która nazywana jest momentem bezwładności, jest z reguły oznaczana literą I i pojawia się w fizyce rozważając moment pędu punktu materialnego, który obraca się wokół osi. Moment pędu L w formie skalarnej zapisuje się następującym wyrażeniem:

L = r * m * v

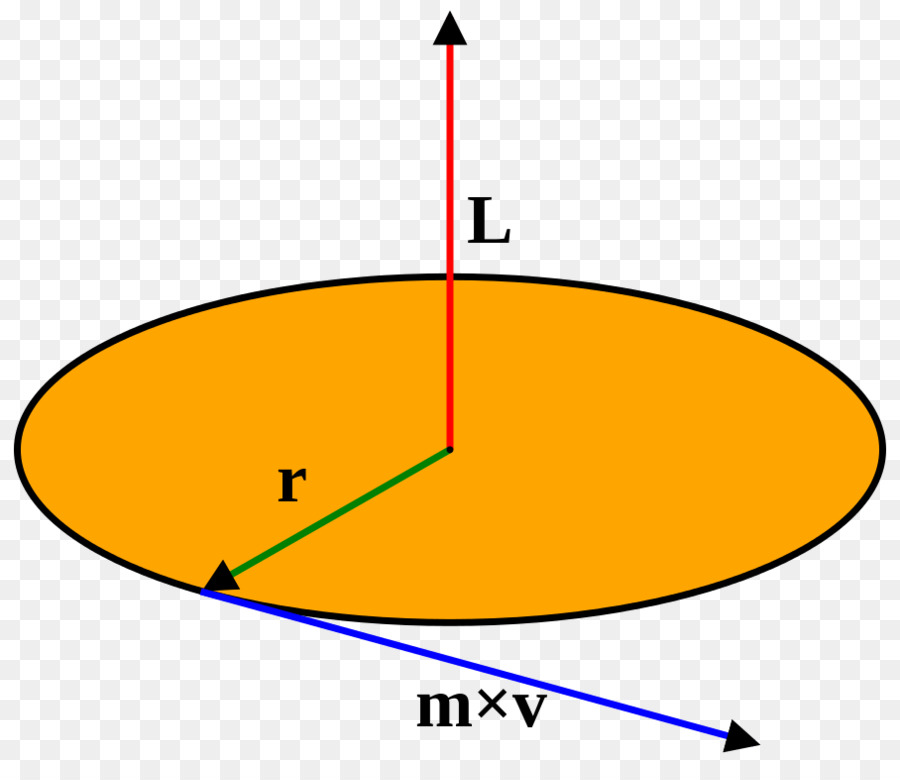
Tutaj r jest odległością do osi punktu materialnego, m jest jej masą, v jest prędkością liniową. Używając zależności tego ostatniego z prędkością kątową ω, uzyskujemy wyrażenie:

L = r ² * m * ω, gdzie ω = v / r

Odpowiadając na pytanie, jaki jest moment bezwładności, należy stwierdzić, że jest to wartość I = r ² * m. Oznacza to, że zależy on od masy obracającego się obiektu, rośnie szybko wraz ze wzrostem odległości od osi i jest mierzony w kg * m ² .

Ogólne wyrażenie na moment bezwładności

Formuła wprowadzona w poprzednim akapicie dla wartości I jest poprawna, jeśli wymiary obiektu są pomijalne w porównaniu do odległości do osi r (Ziemia obraca się wokół naszej gwiazdy). Jeżeli wymiary liniowe obiektu staną się porównywalne z odległością r, wówczas należy obliczyć I, aby zastosować bardziej ogólny wzór, podany poniżej:

I = ∫ _m (r ² * dm)

Pokazuje to, że całka jest momentem bezwładności punktu materialnego. Suma wszystkich momentów z punktów o masie dm jest całkowitym momentem bezwładności I dla całego ciała.

Ta formuła jest potężnym narzędziem do określania ciała I o absolutnie dowolnym kształcie. Zgodnie ze wzorem, wartość I jest addytywna, to znaczy pozwala rozdzielić ciało na oddzielne części, obliczyć momenty bezwładności, a następnie dodać wyniki, aby uzyskać wartość ciała I.

Fizyczne znaczenie I

Wiedząc, co jest moment bezwładności, trzeba powiedzieć kilka słów o tym, jak jego wartość wpływa na zachowanie i charakterystykę rotacji rzeczywistych obiektów.

Duża wartość I prowadzi do tego, że ciało bardzo trudno obraca się wokół osi. Aby to zrobić, musisz wykonać znaczną pracę i podjąć znaczące wysiłki. Przykładem nadwozia o dużym I jest koło zamachowe samochodu - ciężki metalowy dysk sztywno zamontowany na wale korbowym silnika. Wręcz przeciwnie, jeśli wartość systemu I jest mała, to można ją szybko rozwinąć i tak szybko i łatwo zatrzymać. Przykładem tego jest aluminiowa obręcz koła rowerowego.

Powyższa dyskusja sugeruje, że moment bezwładności charakteryzuje się bezwładnością procesu rotacji, to znaczy pełni tę samą rolę, co masa ciała, gdy zostaje przyłożona do niego siła w celu przyspieszenia.

Różnica między masą a momentem bezwładności leży nie tylko w jednostkach miary, ale także w tym, że ta ostatnia jest funkcją układu obrotowego, a nie tylko geometrii ciała i jego masy.

Moment bezwładności wokół osi obrotu przecinającej środek masy pręta

Rozważ przykład zastosowania integralnej formuły do ​​rozwiązywania rzeczywistych problemów. Przede wszystkim rozwiązujemy prosty problem: cienki pręt o długości l i masie m. Oś obraca się prostopadle do tego pręta przez środek masy obiektu. Konieczne jest określenie wartości I dla tego systemu.

Piszemy ogólny wzór na bezwładność momentu pręta wokół osi, mamy:

I = ∫ _m (r ² * dm)

Ponieważ oś jest prostopadła do ciała, o którym mowa, a sam pręt ma nieskończenie małą grubość, możliwe jest jego pocięcie na cienkie warstwy za pomocą płaszczyzn równoległych do osi. W tym przypadku stwierdzamy, że element masy dm może być reprezentowany przez następujące równanie:

dm = ρ * s * dr

Tutaj ρ jest gęstością materiału, S jest przekrojem, który jest stały i dąży do zera (pręt jest nieskończenie cienki). Zastąp to wyrażenie w ogólnej formule:

I = ρ * S * ∫ ^{+ l / 2} _{-l / 2} (r ² * dr)

Zauważ, że podstawione limity całkowania dla r odpowiadają stanowi problemu (oś dzieli pręt na dwie równe części). Wykonując integrację otrzymujemy:

I = ρ * S * (r 3/3) | ^{+ l / 2} _{-l / 2} = m * l 2/12, gdzie m = ρ * S * l

Tak więc moment bezwładności cienkiego pręta, gdy oś przechodzi przez środek masy, jest 12 razy mniejszy niż punkt materialny tej samej masy usytuowany w odległości l od osi.

Wartość I dla pręta z osią obrotu na końcu obiektu

Zastanów się, jaki jest moment bezwładności, w nieco innej sytuacji. Mamy ten sam obiekt (cienki pręt), ale teraz oś przechodzi przez koniec. Jak zmieni się moment bezwładności w tym przypadku? Stosując tę ​​samą metodę podziału pręta i późniejszej integracji, jak w poprzednim paragrafie, otrzymujemy:

I = ρ * S * ∫ ^l ₀ (r ² * dr)

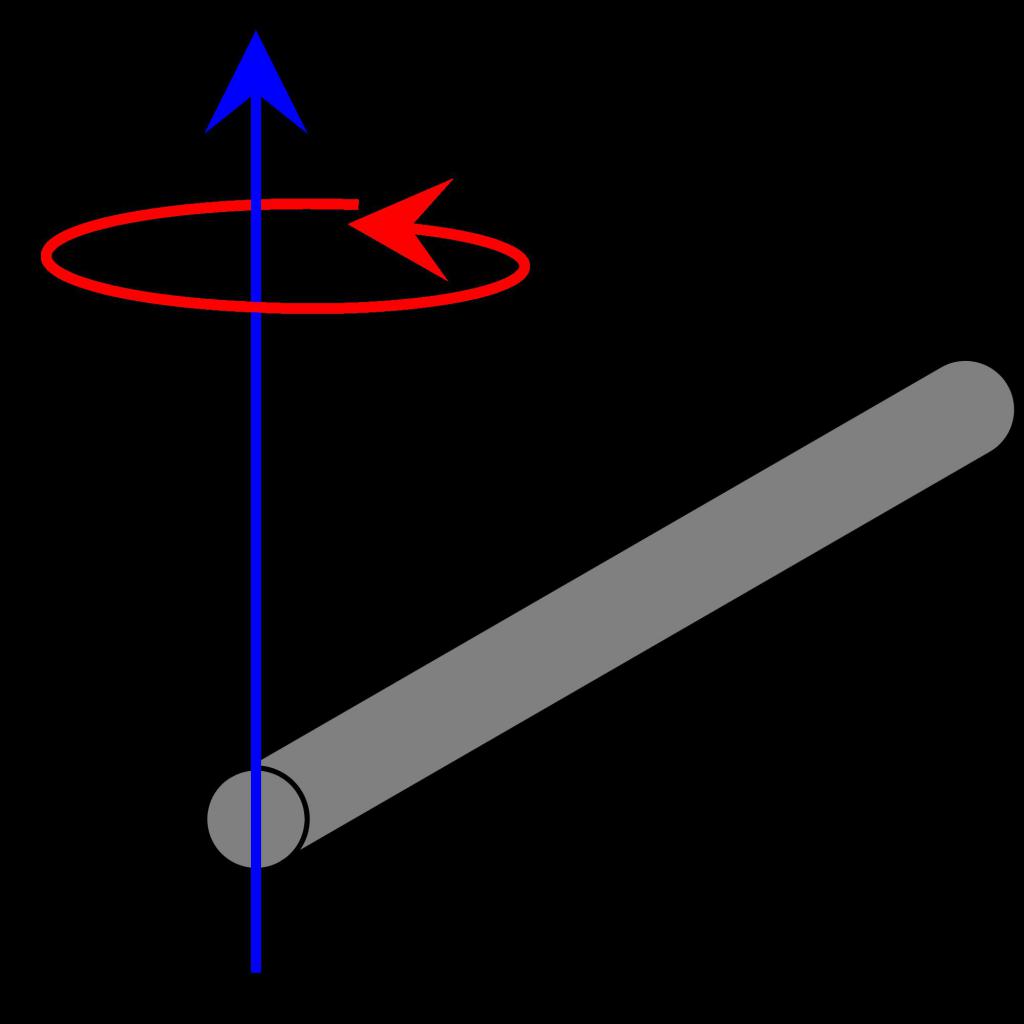
Zauważ, że zmieniły się tylko granice integracji. Rozwiązaniem jest następująca równość:

I = m * l 2/3

Wyrażenie pokazuje, że ten sam pręt będzie miał 4-krotność dużego momentu bezwładności (trudniej się obracać), jeśli oś obrotu zostanie przesunięta ze środka do krawędzi.

Rozważając rozwiązanie tych dwóch problemów, należy wyciągnąć ważny wniosek: przy obliczaniu wartości I niemożliwe jest zredukowanie całej masy obiektu do jego środka i wykonanie obliczeń jak dla punktu materialnego. Obliczenia należy przeprowadzać tylko za pomocą wyrażenia integralnego.

Cenię szprychowe koło

Moment bezwładności koła można wyznaczyć za pomocą właściwości addytywności rozpatrywanej ilości. W tym celu zdemontuj koło w oddzielnych częściach, które reprezentują szprychy i obręcz. Ponieważ igła jest cienkim prętem, a jego oś obrotu przechodzi przez koniec, wówczas obowiązuje wzór uzyskany w poprzednim akapicie.

Jeśli chodzi o obręcz koła, moment bezwładności jest podobny do momentu punktu materialnego znajdującego się w odległości od promienia koła i mającego masę obręczy.

Dodając momenty bezwładności wszystkich elementów, otrzymujemy:

I = n * m _c * r 2/3 + m _o * r ²

Tutaj m _c i m _o są odpowiednio szprychami i masami obręczy, n jest liczbą szprych. Jeśli wszystkie szprychy ważą znacznie mniej niż felga, wówczas bezwładność koła będzie równa:

I = m _o * r ^2, jeśli n * m _c < o

Znajomość wartości I dla koła jest ważna przy obliczaniu prędkości kątowej i momentu pędu obrotu kół dowolnego pojazdu (samochodu, roweru).