Jaka jest zasada farmy?
Wiek XVII charakteryzował się szybkim rozwojem w Europie specjalnej sekcji fizyki - optyki. Prawa odbicia i załamania były otwarte na światło, a zasada Fermata pokazała, dlaczego mają odpowiednią formę matematyczną. Zobaczmy bardziej szczegółowo, czym jest ta zasada.
Zjawiska refrakcji i odbicia

Poprzez odbicie rozumieją zjawisko, w którym światło, rozprzestrzeniające się w substancji przezroczystej, napotyka przeszkodę na swojej drodze i radykalnie zmienia jej trajektorię. Wszelkie przeszkody mogą być dowolne: płynne lub stałe, przezroczyste i nieprzejrzyste.
Zjawisko odbicia jest znane od czasów starożytnych. Zgodnie z historycznymi dowodami, prawa refleksji zostały już sformułowane przed naszą erą. I w pierwszym wieku naszej ery egipski filozof Heron z Aleksandrii wyraził ideę trajektorii światła, którą francuski Pierre Fermat wykorzystał później do sformułowania swojej zasady.

Zjawiskiem załamania jest pęknięcie linii prostej, wzdłuż której światło się porusza, gdy przecina powierzchnię oddzielając dwa przezroczyste materiały. Zwróć uwagę, że w przypadku odbicia wiązka przesuwa się w jednym przezroczystym materiale lub, jak to mówią, w jednym medium.
Pierwsze sformułowanie praw refrakcji przypisuje się perskim matematykom z X wieku, pewnemu Ibnu Sahlowi, który w swoich pracach polegał na dziełach Klaudiusza Ptolemeusza (I-II wiek ne). Na przełomie końca XVI - początku XVII wieku holenderski naukowiec Snell, podsumowując wyniki wielu eksperymentów ze światłem, sformułował w formie matematycznej drugie prawo załamania, które teraz nosi jego nazwisko. Snell wydał swoje sformułowanie w kategoriach odległości, a nie kątów, jak to jest teraz zwyczajowe. Nowoczesny wygląd prawa refrakcji dał już Rene Descartes.
Prawa propagacji światła w przezroczystych mediach
Przed przystąpieniem do rozważania zasady Fermata należy sformułować prawa załamania światła i odbicia światła. W przypadku każdego z tych zjawisk zwyczajowo wyróżnia się dwa prawa. Poniżej są one połączone parami:
- Trajektoria wiązki, gdy przecina ona interfejs między dwoma mediami, zawsze leży w tej samej płaszczyźnie, co normalna do płaszczyzny tej granicy. Ewentualna trajektoria promienia tworzona jest w ogólnym przypadku z trzech części: wiązki padającej, załamanej i odbijanej.
- Jeśli kąt między padającym wiązką światła i normalnym jest nazywany θ 1 , to ten sam kąt, ale dla odbitej wiązki, zapisywany jest jako θ 2 , a załamany kąt θ 3 , wtedy drugie prawo będzie wyglądało jak:
- dla odbicia: θ 1 = θ 2 ;
- dla refrakcji: n 1 * sin (θ 1 ) = n 2 * sin (θ 3 ).
W tych wzorach n 1 i n 2 są współczynnikami załamania światła w przezroczystych mediach 1 i 2. Współczynnik załamania z definicji oblicza się w następujący sposób:
n = c / v.
Tutaj v i c to prędkości ruchu wiązki światła w ośrodku iw próżni.
Formułowanie zasady gospodarstwa

Pierre Fermat był jednym ze słynnych matematyków i prawników Francji w pierwszej połowie XVII wieku. Zasada, która nosi jego imię, sformułował w 1662 roku, czyli pół wieku po tym, jak Snell odkrył swoje prawo do refrakcji.
Krótko mówiąc, zasada Fermata może być sformułowana w następujący sposób: światło, poruszając się w absolutnie dowolnym przezroczystym medium, wybiera taką trajektorię, którą przejdzie w najkrótszym czasie.
W rzeczywistości to sformułowanie nie różni się od tego, które Heron Aleksandryjski zrobił półtora tysiąca lat wcześniej dla zjawiska odbicia. Niemniej jednak Francuz upowszechnił wszystkie zjawiska związane ze światłem i pokazał, w jaki sposób prawa refrakcji i refleksji można wyprowadzić z tej zasady.
Zakończenie 1. ustawy o refleksji
Korzystając z zasady Fermata, prawa odbicia zostaną uzyskane matematycznie. Aby to zrobić, rozważ poniższy rysunek.
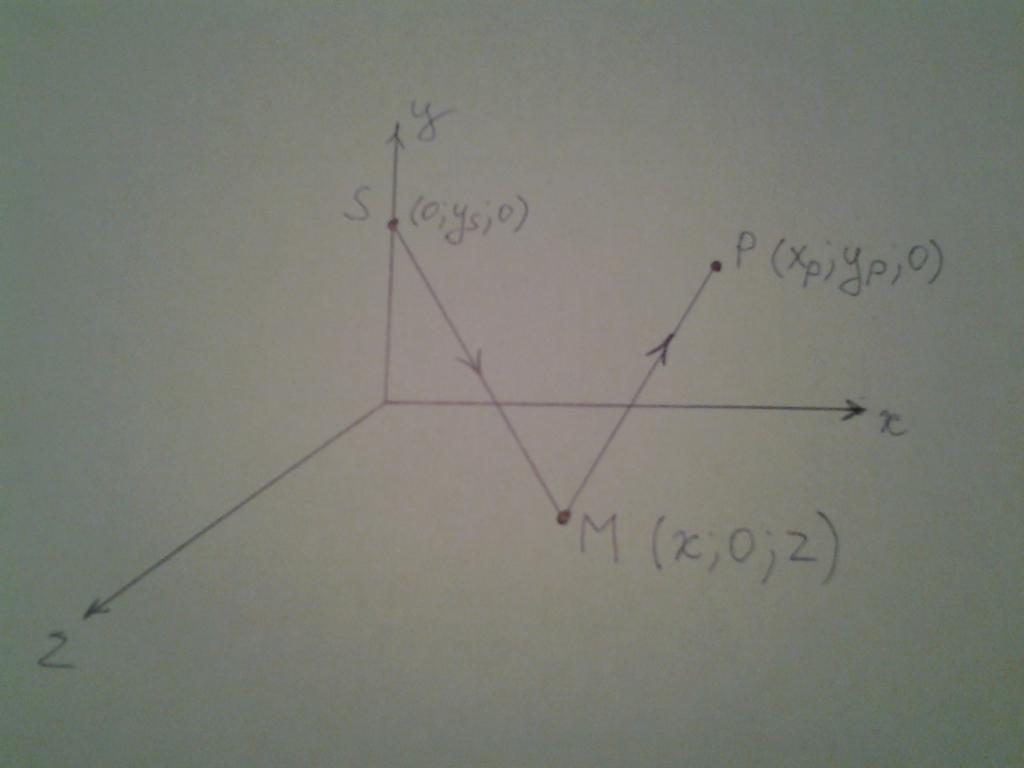
Tutaj pokazano, że wiązka wychodzi z punktu S, który leży na osi Y. Następnie odbija się od płaszczyzny Xz w pewnym nieznanym punkcie M. Po odbiciu promień przesuwa się do punktu P leżącego na płaszczyźnie xy. Wybrana pozycja punktów S i P nie wpływa na ogólność dalszego rozumowania, a jedynie upraszcza obliczenia matematyczne.
Tak więc zapisujemy współrzędne każdego punktu:
S (0; yS; 0);
M (x; 0; z);
P (x P ; y P ; 0).
Współrzędne pozycji punktów S i P są znane. Zadanie polega na znalezieniu takiego punktu M, który będzie odpowiadał rzeczywistej drodze SMP przechodzącej przez wiązkę światła. Przyjmujemy również, że rozpatrywana przestrzeń jest jednorodna, tj. Prędkość światła w dowolnym punkcie jest wartością stałą.
Zgodnie z zasadą Fermata trajektoria światła SMP przejdzie w najkrótszym czasie, jeśli jest najkrótsza z możliwych. Piszemy jego długość:
SM = √ (x 2 + y S2 + z2); MP = √ ((xxP) 2 + yP2 + z2);
SMP = √ (x 2 + y S 2 + z 2 ) + √ ((xx P ) 2 + y P 2 + z 2 ).
Aby obliczyć minimalną długość SMP, konieczne jest znalezienie częściowych pochodnych w odniesieniu do x i z (nieznanych współrzędnych punktu M) i zrównanie uzyskanych wyników do zera.
Najpierw znajdujemy pochodną cząstkową względem z. Mamy:
∂ (SMP) / ∂z = z / √ (x 2 + y S 2 + z 2 ) + z / √ ((xx P ) 2 + y P 2 + z 2 ) = 0.
Równość ta ma jeden rdzeń, gdy z = 0. Innymi słowy, punkt M leży na osi x, to znaczy w tej samej płaszczyźnie, co punkty P i S (płaszczyzna xy). Z tego wynika, że przywrócona normalna do płaszczyzny Xz, w której, ze względu na stan problemu, znajduje się punkt M, będzie leżeć z SM i MP w tej samej płaszczyźnie (xy). To jest pierwsza zasada refleksji.
Zakończenie 2. prawa refleksji
Kontynuuj obliczanie poprzedniej pozycji. Jak już wspomniano, obecnie konieczne jest znalezienie częściowej pochodnej w odniesieniu do x. Mamy:
∂ (SMP) / ∂x = x / √ (x 2 + y S 2 + z 2 ) + (xx P ) / √ ((xx P ) 2 + y P 2 + z 2 ) = 0.
Napiszemy ostatnią równość w postaci:
x / SM + (xx P ) / MP = 0 =>
x / SM = (x P -x) / MP.
Relacje uzyskane w każdej części równości są sinusami kątów z wierzchołkiem w punktach S i P. Jeśli teraz przywrócimy normalne do płaszczyzny xz przez punkt M, wtedy zaznaczone kąty będą odpowiadały kątom padania (między SM a normalnym) i odbiciom (między MP a normalnym) .
W ten sposób, zgodnie z zasadą Fermata, uzyskaliśmy również drugą zasadę odbicia światła.
Wniosek prawa załamania Snell
Pokażmy teraz, w jaki sposób prawo załamania światła można wyprowadzić z zasady Fermata. Aby to zrobić, rozważ zdjęcie podobne do poprzedniego.
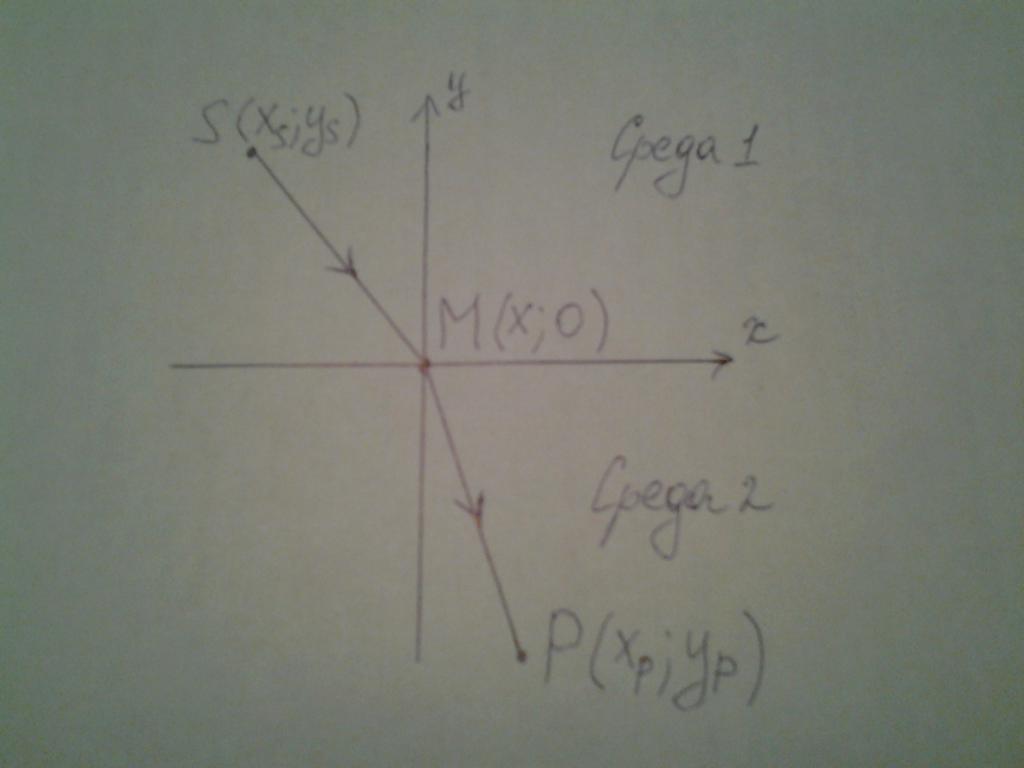
Dla uproszczenia rozważymy przypadek na płaszczyźnie XY. Zapisujemy współrzędne źródła S i odbiornika P light, które znajdują się w różnych środowiskach:
S ( xS , yS);
M (x; 0);
P (x P ; y P ).
Znajdźmy nieznaną współrzędną punktu M. Współrzędna y = 0 jest dla niej dokładnie znana, ponieważ to właśnie na granicy mediów (oś x) zmienia się prędkość światła. Długości segmentów SM i MP są równe:
SM = √ (xxS) 2 + yS2);
MP = √ (x P -x) 2 + y P2 ).
Całkowity czas, jaki światło spędza na trajektorii SMP, będzie równy:
t = SM / v 1 + MP / v 2 .
Tutaj v 1 i v 2 są prędkościami wiązki w odpowiednich mediach. Aby znaleźć minimalny czas ruchu, należy pobrać całkowitą pochodną w odniesieniu do zmiennej x i zrównaczyć ją do zera. Otrzymujemy:
dt / dx = (xx S ) / (√ (xx S ) 2 + y S 2 ) * v 1 ) - (x P -x) / (√ (x P -x) 2 + y P 2 ) * v 2 ) = 0 =>
(xx S ) / (SM * v 1 ) = (x P -x) / (MP * v 2 ).
Wykorzystując funkcje sinusoidalne kąta padania θ 1 i załamania θ 3 , otrzymujemy:
sin (θ 1 ) / v 1 = sin (θ 3 ) / v 2 .
Aby doprowadzić uzyskaną równość do prawa Snell'a w dogodnej formie (poprzez współczynniki załamania mediów), konieczne jest pomnożenie lewej i prawej strony przez prędkość światła c.

Tak więc zastosowanie zasady Fermata ułatwia wyprowadzenie praw dla głównych zjawisk ruchu wiązki światła w przezroczystych materiałach.
Ruch światła w niejednorodnym medium
Przypadki rozważane powyżej zakładają, że materiał jest homogeniczny, a wiązka światła zachowuje swoją prędkość, gdy się porusza. W przypadku mediów niejednorodnych obowiązuje następująca równość:
L = ∫n (x, y, z) * dl.
Ta całka jest pobierana wzdłuż trajektorii światła. Różnica dl jest segmentem ścieżki, dla której medium zachowuje swoją jednorodność. Wartość n (x, y, z) jest lokalnym współczynnikiem załamania.
Zanotowana całka nazywana jest zwykle całką ścieżki optycznej. Zasada farmy dla ścieżki optycznej obejmuje znalezienie ekstremów dla L.
Uogólnione sformułowanie rozważanej zasady
Zasada minimalnego czasu dla przemieszczania się światła ma charakter bardziej ogólny. Obecnie uogólniona zasada Fermata jest sformułowana w następujący sposób: światło wybiera trajektorię podczas ruchu, która odpowiada skrajności ścieżki optycznej.
Ekstremum funkcji, zgodnie z matematyczną definicją, to punkt minimalny, maksymalny i punkt przegięcia. Ogólna zasada Fermata spełnia wszystkie te wartości, tzn. Trajektoria światła niekoniecznie musi być minimalna, może to być zarówno maksymalny, jak i odpowiadający punkt przegięcia ścieżki optycznej.
Analogia krajowa do rozważanej zasady
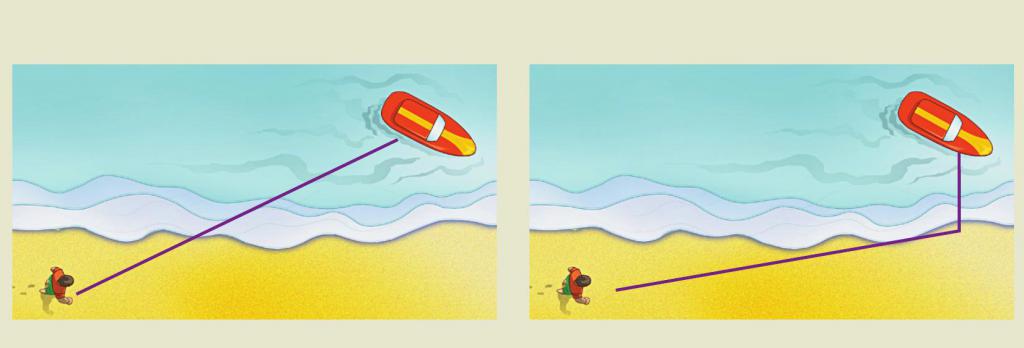
Ogólna zasada Fermata jest z kolei szczególnym przypadkiem tak zwanej zasady najmniejszego działania. Tutaj nie podamy odpowiednich definicji i ich matematycznych sformułowań, jednak pokażmy, gdzie można zastosować zasadę zaproponowaną przez Francuzów.
Służy do rozwiązania prostego, na pierwszy rzut oka, codziennego zadania: na przykład osoba tonie w morzu w pobliżu plaży. W jaki sposób ratownik powinien przenieść się na brzeg, aby uratować tonącego? Oczywiście powinien przybyć na ratunek w jak najmniejszym czasie. Ponieważ prędkość poruszania się ratownika na plaży jest większa niż na wodzie, powinien biegać w pewnej odległości wzdłuż brzegu, a dopiero potem wskoczyć do wody i pływać. Oznacza to, że zadanie sprowadza się do zastosowania zasady Fermata, w której rolę promienia światła odgrywa ratownik.
Zauważ, że rozwiązanie tego problemu nie jest proste, ponieważ w jego procesie pojawiają się równania czwartego stopnia.
Tak więc zasada Fermata jest narzędziem do uzyskania podstawowych praw propagacji światła. Jednak nie jest to kwestia fundamentalna. Można powiedzieć, że wynika to z zasady Huygensa o źródłach wtórnych fal sferycznych.