Jaki jest współczynnik załamania światła szkła? A kiedy trzeba to wiedzieć?

Podczas rozwiązywania problemów w optyce często wymagane jest poznanie współczynnika załamania światła, wody lub innej substancji. W różnych sytuacjach mogą być uwzględnione wartości bezwzględne i względne tej wartości.

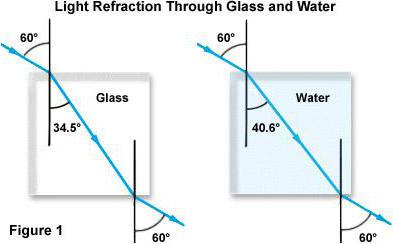
Dwa rodzaje współczynnika załamania światła

Po pierwsze, fakt, że liczba ta pokazuje: jak ten lub ten przezroczysty nośnik zmienia kierunek propagacji światła. I fala elektromagnetyczna może pochodzić z próżni, a następnie współczynnik załamania światła szkła lub innej substancji będzie nazywany absolutnym. W większości przypadków jego wartość mieści się w zakresie od 1 do 2. Tylko w bardzo rzadkich przypadkach współczynnik załamania jest większy niż dwa.

Jeśli przedtem istnieje gęstsze środowisko niż próżnia, to już mówią o względnej wartości. Jest on obliczany jako stosunek dwóch wartości bezwzględnych. Na przykład względny współczynnik załamania światła szkło wodne będzie równe szczególnym wartościom absolutnym dla szkła i wody.

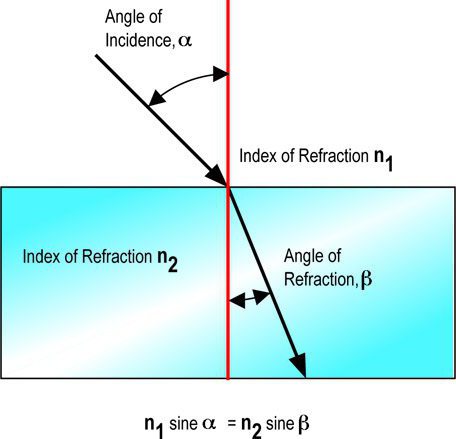
W każdym razie jest to oznaczone łacińską literą "en" - n. Wartość tę uzyskuje się, dzieląc się nawzajem z tą samą wartością, dlatego jest to po prostu współczynnik, który nie ma nazwy.

Jakiej formuły można użyć do obliczenia współczynnika załamania światła?

Jeśli przyjmiemy kąt padania jako "alfa", a kąt załamania jest oznaczony jako "beta", wówczas wzór na wartość bezwzględną współczynnika załamania wygląda następująco: n = sin α / sin β. W literaturze anglojęzycznej często można znaleźć inne oznaczenie. Gdy kąt padania wynosi i, a załamanie jest r.

Istnieje jeszcze jedna formuła obliczania współczynnika załamania światła w szkle i innych przezroczystych mediach. Jest to związane z prędkością światła w próżni i przez nią, ale już w rozpatrywanej substancji.

Wtedy wygląda to tak: n = c / νλ. Tutaj c jest prędkością światła w próżni, ν jest prędkością w przezroczystym medium, a λ jest długością fali.

Co decyduje o współczynniku załamania światła?

Wyznacza ją prędkość, z jaką światło porusza się w badanym medium. Powietrze pod tym względem jest bardzo bliskie próżni, dlatego propagowane w niej fale świetlne praktycznie nie odbiegają od pierwotnego kierunku. Dlatego też, jeśli określa się współczynnik załamania światła szklanego lub jakiejkolwiek innej substancji graniczącej z powietrzem, to zwykle przyjmuje się, że jest to próżnia.

Każde inne medium ma swoją własną charakterystykę. Mają różne gęstości, mają swoją własną temperaturę, a także naprężenia sprężyste. Wszystko to wpływa na wynik załamania światła przez materię.

Ostatnią rolą w zmianie kierunku propagacji fali nie jest charakterystyka światła. Białe światło składa się z różnych kolorów, od czerwonego do fioletowego. Każda część widma jest załamywana na swój sposób. Co więcej, wartość wskaźnika dla fali czerwonej części widma będzie zawsze mniejsza niż reszta. Na przykład współczynnik załamania światła szkła TF-1 zmienia się odpowiednio z 1,6421 do 1,67298 z czerwonej do fioletowej części widma.

Przykłady wartości dla różnych substancji

Oto wartości bezwzględne, to znaczy współczynnik załamania, gdy wiązka przechodzi z próżni (która jest równa powietrzu) ​​przez inną substancję.

Wartości te będą wymagane, jeśli konieczne jest określenie współczynnika załamania światła w stosunku do innych mediów.

Jakie inne wartości są używane przy rozwiązywaniu problemów?

Pełna refleksja. Obserwuje się, gdy światło przechodzi z gęstszego ośrodka do mniej gęstego. Tutaj, pod pewnym kątem padania, załamanie zachodzi pod kątem prostym. Oznacza to, że wiązka przesuwa się wzdłuż granicy dwóch mediów.

Maksymalny kąt całkowitego odbicia jest jego minimalną wartością, przy której światło nie wchodzi w mniej gęsty ośrodek. Mniej niż to - pojawia się refrakcja, a więcej - odbicie w tym samym środowisku, z którego przemieszczało się światło.

Numer problemu 1

Stan Współczynnik załamania szkła wynosi 1,52. Konieczne jest określenie kąta ograniczającego, w którym światło z powierzchni międzyfazowej jest całkowicie odbite: szkło z powietrzem, woda z powietrzem, szkło z wodą.

Decyzja.

Będziesz musiał użyć tych współczynników załamania dla wody podanej w tabeli. Do powietrza przyjmuje się równe jeden.

Rozwiązanie we wszystkich trzech przypadkach jest zredukowane do obliczeń za pomocą następującego wzoru:

sin α ₀ / sin β = n ₁ / n ₂ , gdzie n ₂ odnosi się do ośrodka, z którego promieniuje światło, i n _1, gdzie penetruje.

Litera a ₀ oznacza kąt graniczny. Wartość kąta β wynosi 90 stopni. Oznacza to, że jego sinus będzie jednym.

W pierwszym przypadku: sin α ₀ = 1 / n _glass , wówczas kąt graniczny jest równy arcusine of 1 / n _glass . 1 / 1,52 = 0,6579. Kąt wynosi 41,14º.

W drugim przypadku, podczas określania arcusine, konieczne jest zastąpienie wartości wskaźnika refrakcji wody. Frakcja 1 / n _wody przyjmie wartość 1 / 1.33 = 0, 7519. Jest to kąt łukowy wynoszący 48,75º.

Trzeci przypadek jest opisany przez stosunek n _wody i n _szkła . Arcsine będzie musiała obliczyć dla frakcji: 1.33 / 1.52, czyli liczbę 0.875. Znajdź wartość kąta granicznego za pomocą swojej arcsine: 61,05º.

Odpowiedź: 41,14 º, 48,75 º, 61,05 º.

Numer problemu 2

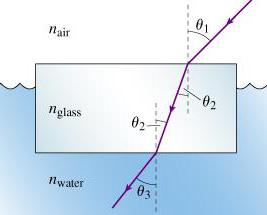
Stan Szklany pryzmat zanurzony jest w naczyniu z wodą. Jego współczynnik załamania wynosi 1,5. Pryzmat jest oparty na trójkąt prostokątny. Większa noga jest prostopadła do spodu, a druga jest równoległa do niej. Strumień światła pada normalnie na górną powierzchnię pryzmatu. Jaki powinien być najmniejszy kąt między poziomą nogą a przeciwprostokątną, aby światło sięgało do nogi prostopadłej do dna naczynia i wychodziło z pryzmy?

Decyzja.

Aby belka opuściła pryzmat w opisany sposób, musi spaść pod ekstremalnym kątem na wewnętrzną krawędź (tę, która jest przeciwprostokątną trójkąta w części pryzmatu). Ten kąt graniczny okazuje się być równy pożądanemu kątowi trójkąta prostokątnego. Z prawa załamywania światła wynika, że ​​sinus kąta granicznego podzielony przez sinus o wartości 90 stopni jest równy stosunkowi dwóch współczynników załamania: wody do szkła.

Obliczenia prowadzą do tej wartości dla kąta granicznego: 62º30'.

Odpowiedź: 62º30'.