Podstawowe pojęcia teorii prawdopodobieństwa i statystyki matematycznej

Matematyka obejmuje cały zestaw obszarów, z których jednym, obok algebry i geometrii, jest teoria prawdopodobieństwa. Istnieją terminy, które są wspólne dla wszystkich tych obszarów, ale oprócz nich istnieją specyficzne, charakterystyczne dla tylko jednego szczególnego "niszowego" słowa, formuły, twierdzenia.

Wyrażenie "teoria prawdopodobieństwa" wywołuje panikę u nieprzygotowanego studenta. Rzeczywiście, wyobraźnia maluje obrazy, gdzie pojawiają się straszne wzory objętościowe, a rozwiązanie jednego problemu zajmuje cały notatnik. Jednak w praktyce sprawy nie są tak straszne: wystarczy zrozumieć znaczenie niektórych terminów i dotrzeć do sedna jakiejś szczególnej logiki rozumowania, aby przestać bać się zadań raz na zawsze. W tym względzie rozważamy podstawowe pojęcia teorii prawdopodobieństwa i statystyki matematycznej - młodej, ale niezwykle interesującej dziedziny wiedzy.

Po co uczyć pojęć

Zadaniem tego języka jest przekazywanie informacji od jednej osoby do drugiej, tak aby je rozumiał, realizował i mógł z niego korzystać. Każda koncepcja matematyczna może być wyjaśniona prostymi słowami, ale w tym przypadku akt wymiany danych zajęłby znacznie więcej czasu. Wyobraź sobie, że zamiast słowa "przeciwprostokątna" zawsze musiałbyś powiedzieć "najdłuższa strona trójkąta prostokątnego" - jest to bardzo niewygodne i długie.

Dlatego ludzie wymyślają nowe terminy dla pewnych zjawisk i procesów. Podstawowe pojęcia teorii prawdopodobieństwa - zdarzenia, prawdopodobieństwo zdarzenia itp. - pojawiły się w ten sam sposób. Aby więc używać formuł, rozwiązywać problemy i stosować umiejętności życiowe, konieczne jest nie tylko zapamiętywanie nowych słów, ale także zrozumienie, co każdy z nich oznacza. Im głębiej stajesz się ich świadomym, zagłębiasz się w znaczenie, im szerszy jest zakres twoich możliwości, tym pełniej postrzegasz świat wokół siebie.

Jakie jest znaczenie tematu

Zapoznajmy się z podstawowymi pojęciami teorii prawdopodobieństwa. Klasyczna definicja prawdopodobieństwa jest następująca: jest to stosunek wyników odpowiadających badaczowi do całkowitej liczby możliwych. Podajmy prosty przykład: kiedy ktoś rzuca kością, może odrzucić jedną z sześciu stron w górę. Łączna liczba wyników wynosi sześć. Prawdopodobieństwo losowo wybranej strony wypadającej wynosi 1/6.

Możliwość przewidywania pojawienia się określonego wyniku jest niezwykle ważna dla różnych specjalistów. Ile wadliwych części jest oczekiwanych w wielu? To zależy od tego, ile wyprodukować. Jakie jest prawdopodobieństwo, że lek pomoże zwalczyć chorobę? Takie informacje są niezbędne. Ale nie traćmy czasu na dodatkowe przykłady i przejdźmy do zbadania nowego obszaru dla nas.

Pierwsza znajomość

Rozważ podstawowe pojęcia teorii prawdopodobieństwa i ich zastosowania. W prawo naturalne Nauki ścisłe, wzory ekonomiczne i terminy przedstawione poniżej są używane wszędzie, ponieważ są bezpośrednio związane ze statystykami i błędami pomiarowymi. Bardziej szczegółowe badanie tego pytania otworzy Ci nowe formuły, które są przydatne do bardziej dokładnych i złożonych obliczeń, ale zacznijmy od prostego.

Jednym z najbardziej podstawowych i podstawowych pojęć teorii prawdopodobieństwa i statystyki matematycznej jest zdarzenie losowe. Wyjaśnij w jasny sposób: ze wszystkich możliwych wyników eksperymentu, tylko jeden jest obserwowany w rezultacie. Nawet jeśli prawdopodobieństwo wystąpienia tego zdarzenia jest znacznie większe niż inne, będzie to przypadkowe, ponieważ teoretycznie wynik mógłby być inny.

Jeśli przeprowadziliśmy serię eksperymentów i uzyskaliśmy pewną liczbę wyników, to prawdopodobieństwo każdego z nich oblicza się za pomocą wzoru: P (A) = m / n. Tutaj m jest to, ile razy w serii testowej widzieliśmy wynik zainteresowania nami. Z kolei n jest całkowitą liczbą wykonanych eksperymentów. Jeśli rzuciliśmy monetą 10 razy i otrzymaliśmy "ogony" 5 razy, to m = 5, a n = 10.

Rodzaje zdarzeń

Zdarza się, że pewne wyniki są przestrzegane w każdej próbie - takie wydarzenie będzie nazywane wiarygodnym. Jeśli to się nigdy nie stanie, zostanie nazwane niemożliwe. Jednak takie zdarzenia nie są wykorzystywane w warunkach problemów dotyczących teorii prawdopodobieństwa. Podstawowe pojęcia, które są o wiele ważniejsze, to wspólne i niekompatybilne wydarzenia.

Zdarza się, że podczas eksperymentu występują jednocześnie dwa zdarzenia. Na przykład rzucamy dwiema kośćmi - w tym przypadku fakt, że jeden miał "sześć" wypadł, nie gwarantuje, że drugi nie spadnie na sekundę. Takie wydarzenia będą nazywane wspólnymi.

Jeśli rzucimy jedną kością, to dwie liczby w tym samym czasie nie będą mogły wypaść nigdy. W takim przypadku wyniki w postaci odrzuconych "jeden", "dwa" itd. Będą uważane za niezgodne zdarzenia. Bardzo ważne jest, aby rozróżnić, które wyniki mają miejsce w każdym konkretnym przypadku - zależy to od tego, jakie formuły zastosować w przypadku znalezienia prawdopodobieństwa. Podstawowe pojęcia teorii prawdopodobieństwa, będziemy nadal studiować kilka akapitów później, gdy weźmiemy pod uwagę cechy dodawania i mnożenia. Bez nich nie da się rozwiązać żadnego problemu.

Kwota i produkt

Załóżmy, że rzucasz kością z przyjacielem, a on ma "czwórkę". Aby wygrać, musisz zdobyć pięć lub sześć. W takim przypadku prawdopodobieństwa zostaną zsumowane: ponieważ prawdopodobieństwo zrzucenia obu liczb wynosi 1/6, odpowiedź będzie wyglądać jak 1/6 + 1/6 = 1/3.

Teraz wyobraź sobie, że rzucasz dwa razy kością, a twój przyjaciel ma 11 punktów. Teraz musisz mieć "sześć" dwa razy z rzędu. Zdarzenia są niezależne od siebie, więc prawdopodobieństwo musi zostać pomnożone: 1/6 * 1/6 = 1/36.

Wśród podstawowych pojęć i twierdzeń teorii prawdopodobieństwa należy zwrócić uwagę na sumę prawdopodobieństw wspólnych zdarzeń, t. to znaczy te, które mogą występować jednocześnie. Wzór dodawania w tym przypadku będzie wyglądał następująco: P (A + B) = P (A) + P (B) - P (AB).

Kombinatoryka

Bardzo często musimy znaleźć wszystkie możliwe kombinacje niektórych parametrów obiektu lub obliczyć liczbę dowolnych kombinacji (na przykład przy wyborze szyfru). Kombinatoryka, która jest ściśle związana z teorią prawdopodobieństwa, pomoże nam w tym. Podstawowe pojęcia obejmują kilka nowych słów, a wiele formuł z tego tematu na pewno się przyda.

Załóżmy, że masz trzy liczby: 1, 2, 3. Potrzebujesz, używając ich, do napisania wszystkich możliwych liczb trzycyfrowych. Ile będzie? Odpowiedź: n! (wykrzyknik oznacza czynnikowy). Kombinacje wielu różnych elementów (liczb, liter itp.), Różniących się tylko kolejnością ich lokalizacji, nazywane są permutacjami.

Częściej jednak spotykamy taką sytuację: jest 10 cyfr (od zera do dziewięciu), z których składa się hasło lub kod. Załóżmy, że ma długość 4 znaków. Jak obliczyć całkowitą liczbę możliwych kodów? Do tego dochodzi specjalna formuła: (n!) / (N - m)!

Biorąc pod uwagę powyższy proponowany warunek problemu, n = 10, m = 4. Ponadto wymagane są tylko proste obliczenia matematyczne. Nawiasem mówiąc, takie kombinacje będą nazywane umieszczaniem.

Wreszcie istnieje pojęcie kombinacji - są to sekwencje, które różnią się od siebie co najmniej jednym elementem. Ich liczba jest obliczana według wzoru: (n!) / (M! (Nm)!).

Matematyczne oczekiwanie

Ważną koncepcją, którą uczeń napotyka już w pierwszych klasach na ten temat, jest matematyczne oczekiwanie. Jest to suma wszystkich możliwych wartości wyników pomnożonych przez ich prawdopodobieństwa. W istocie jest to średnia liczba, którą możemy przewidzieć jako wynik testu. Na przykład istnieją trzy wartości, dla których prawdopodobieństwa podano w nawiasach: 0 (0,2); 1 (0,5); 2 (0.3). Oblicz oczekiwanie: M (X) = 0 * 0,2 + 1 * 0,5 + 2 * 0,3 = 1,1. Zatem z proponowanego wyrażenia możemy zauważyć, że ta wartość jest stała i nie zależy od wyniku testu.

Ta koncepcja jest używana w wielu formułach i będziesz ją wielokrotnie spotykać w przyszłości. Łatwo z nim pracować: oczekiwanie sumy jest równe sumie maty. oczekiwania - M (X + Y) = M (X) + M (Y). To samo dotyczy produktu: M (XY) = M (X) * M (Y).

Rozproszenie

To musi pochodzić ze szkolnego kursu fizyki, o którym pamiętasz, że rozproszenie się rozprasza. Jakie jest jego miejsce wśród podstawowych pojęć teorii prawdopodobieństwa?

Spójrz na dwa przykłady. W jednym przypadku podajemy: 10 (0,2); 20 (0,6); 30 (0,2). W drugim - 0 (0,2); 20 (0,6); 40 (0,2). Matematyczne oczekiwanie w obu przypadkach będzie takie samo, jak więc możemy porównać te sytuacje? Wszakże widzimy gołym okiem, że rozprzestrzenianie wartości w drugim przypadku jest znacznie większe.

W tym celu wprowadzono pojęcie dyspersji. Aby to uzyskać, musisz obliczyć oczekiwanie sumy różnic każdej zmiennej losowej i oczekiwanie. Weź liczby z pierwszego przykładu zapisanego w poprzednim akapicie.

Najpierw obliczamy oczekiwanie: M (X) = 10 * 0,2 + 20 * 0,6 + 30 * 0,2 = 20. Następnie wartość wariancji: D (X) = 40.

Kolejną z podstawowych koncepcji statystyki i teorii prawdopodobieństwa jest odchylenie standardowe. Oblicz to jest bardzo proste: wystarczy wziąć pierwiastek kwadratowy z dyspersji.

Tutaj możemy zauważyć tak prosty termin, jak zakres. Ta wartość wskazuje różnicę między wartością maksymalną i minimalną w próbce.

Statystyki

Niektóre podstawowe koncepcje szkolne są często używane w nauce. Dwa z nich to średnia arytmetyczna i mediana. Na pewno pamiętasz, jak znaleźć swoje wartości. Ale na wszelki wypadek, pamiętamy: średnia arytmetyczna jest sumą wszystkich wartości podzielonych przez ich liczbę. Jeśli wartość wynosi 10, dodajemy je i dzielimy przez 10.

Mediana ma kluczowe znaczenie dla wszystkich możliwych. Jeśli mamy nieparzystą liczbę wartości, piszemy je w porządku rosnącym i wybieramy ten, który był w środku. Jeśli mamy parzystą liczbę wartości, bierzemy dwa centralne i dzielimy przez dwa.

Dwie kolejne wartości, znajdujące się między wartością środkową a dwiema skrajnymi - wartościami maksymalnymi i minimalnymi zbioru, nazywane są kwartyliami. Są one obliczane w ten sam sposób - przy nieparzystej liczbie elementów bierze się liczbę znajdującą się w środku rzędu, a nawet - połowę sumy dwóch elementów centralnych.

Istnieje również specjalny wykres, w którym można zobaczyć wszystkie wartości próbki, jej zakres, medianę, odstępy między kwartałami, a także wartości odstające - wartości, które nie pasują do błędu statystycznego. Powstały obraz ma bardzo specyficzną (a nawet nie matematyczną) nazwę - pudełko z wąsami.

Dystrybucja

Dystrybucja dotyczy także podstawowych pojęć teorii prawdopodobieństwa i statystyki matematycznej. W skrócie, jest to podsumowanie wszystkich zmiennych losowych, które możemy zobaczyć w wyniku testu. Głównym parametrem jest tutaj prawdopodobieństwo wystąpienia każdej określonej wartości.

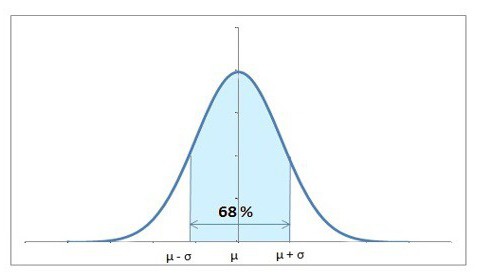Rozkład normalny to taki, który ma jeden centralny pik, w którym umiejscowiona jest najczęściej występująca wartość. Z niego łuki rozchodzą się coraz rzadziej. Ogólnie rzecz biorąc, harmonogram z boku wygląda jak "slajd". W przyszłości dowiesz się, że centralne twierdzenie graniczne, które jest fundamentalne dla teorii prawdopodobieństwa, jest ściśle związane z tym rodzajem rozkładu. Opisuje prawa, które są ważne dla rozważanych przez nas dziedzin matematyki, które są bardzo użyteczne dla różnych obliczeń.

Ale wracając do tematu. Istnieją jeszcze dwa rodzaje dystrybucji: asymetryczne i multimodalne. Pierwszy wygląda jak połowa "normalnego" wykresu, tj. Łuk spada tylko w jednym kierunku od wartości szczytowej. Wreszcie, dystrybucja multimodalna to taka, która ma kilka "górnych" wartości. Harmonogram następnie spada, a potem się podnosi. Największa wartość częstotliwości w dowolnej dystrybucji nazywana jest trybem. Jest to również jedno z podstawowych pojęć teorii prawdopodobieństwa i statystyki matematycznej.

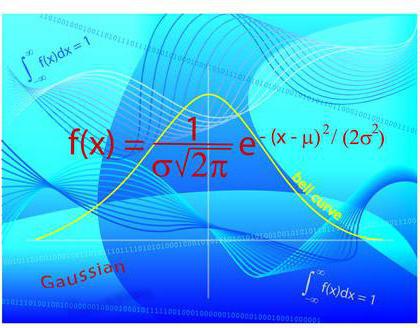
Rozkład Gaussa

Rozkład Gaussa, czyli normalny, to taki, w którym odchylenie obserwacji od średniej podlega pewnemu prawu.

W skrócie, główny rozproszenie wartości próbek wykładniczo ma tendencję do trybu - najczęstszego z nich. Mówiąc dokładniej, 99,6% wszystkich wartości mieści się w granicach trzech standardowych odchyleń (pamiętaj, spojrzeliśmy na powyższą koncepcję?).

Rozkład Gaussa jest jedną z podstawowych koncepcji teorii prawdopodobieństwa. Za jej pomocą można zrozumieć, czy dany element zalicza się do kategorii "typowej" według jednego lub drugiego parametru - tak ocenia się wysokość i wagę osoby w zależności od wieku, poziomu rozwoju intelektualnego, stanu psychicznego i wielu innych.

Jak złożyć wniosek

Co ciekawe, "nudne" dane matematyczne można wykorzystać na swoją korzyść. Na przykład jeden młody człowiek zastosował teorię prawdopodobieństwa i statystyki, aby wygrać kilka milionów dolarów w ruletce. To prawda, że ​​musieliśmy się do tego przygotować - w ciągu kilku miesięcy nagraliśmy wyniki gier w różnych kasynach.

Po analizie stwierdził, że jedna z tabel jest lekko nachylona, ​​co oznacza, że ​​pewna liczba wartości pojawia się statystycznie znacznie częściej niż inne. Trochę kalkulacji, cierpliwości - a teraz właściciele instytucji są zaintrygowani, myśląc o tym, jak dana osoba może mieć tyle szczęścia.

Istnieje wiele codziennych codziennych zadań, których nie da się rozwiązać bez odwoływania się do statystyk. Na przykład, jak określić, ile sklepów zamówić na ubrania o różnych rozmiarach: S, M, L, XL? Aby to zrobić, należy przeanalizować, kto często kupuje ubrania w mieście, w okolicy, w pobliskich sklepach. Jeśli takie informacje nie zostaną uzyskane, właściciel ryzykuje utratą dużych pieniędzy.

Wniosek

Przyjrzeliśmy się wielu podstawowym pojęciom teorii prawdopodobieństwa: testowi, zdarzeniu, permutacji i umiejscowieniu, oczekiwaniu i wariancji, modzie i rozkładowi normalnym ... Ponadto zbadaliśmy szereg formuł, które poświęcono ponad miesiącowi studiów.

Nie zapominajcie: matematyka jest niezbędna w studiowaniu ekonomii, nauk przyrodniczych, technologii informacyjnej, inżynierii specjalności. Statystyka jako jeden z jej obszarów również nie może być uniknięta.

Teraz to zależy od Ciebie: ćwicz, rozwiązuj problemy i przykłady. Nawet podstawowe pojęcia i definicje teorii prawdopodobieństwa zostaną zapomniane, jeśli nie poświęcić czasu na powtórzenie. Ponadto poniższe formuły będą w dużej mierze opierać się na tych, które rozważaliśmy. Dlatego staraj się je pamiętać, tym bardziej, że nie ma ich zbyt wielu.