Podstawowa kinematyka i formuły

Aby zrozumieć, co mechanika się uczy, należy zastanowić się, co oznacza ruch w najogólniejszym sensie. Znaczenie tego słowa oznacza zmianę czegoś. Na przykład ruch polityczny opowiada się za równością różnych grup ludności, niezależnie od ich rasy. Wcześniej nie było, potem coś się zmieniło i teraz wszyscy mają równe prawa. Ten ruch cywilizacyjny naprzód. Inny przykład to ekologiczne. W przeszłości, wychodząc na zewnątrz, nikt nie myślał o tym, co pozostawia za sobą. Dziś każda cywilizowana osoba odbierze go za sobą i zabierze go do wyznaczonego miejsca do dalszej utylizacji.

Coś podobnego można zaobserwować w mechanice. Dzięki ruch mechaniczny zmiany pozycji ciała w przestrzeni w stosunku do innych obiektów w czasie. Głównym zadaniem mechaniki jest wskazanie, gdzie w danym momencie znajduje się obiekt, biorąc pod uwagę nawet ten, który jeszcze nie dotarł. To znaczy, aby przewidzieć pozycję ciała w danym czasie, a nie tylko dowiedzieć się, gdzie dokładnie w przestrzeni było w przeszłości.

Kinematyka to sekcja mechaniki badająca ruch ciała bez analizy jego przyczyn. Oznacza to, że uczy nie tłumaczyć, ale opisywać. Chodzi o to, aby wymyślić sposób, za pomocą którego można ustawić pozycję ciała w dowolnym momencie. Podstawowe pojęcia związane z kinematyką to prędkość, przyspieszenie, odległość, czas i ruch.

Trudności w opisywaniu ruchu

Pierwszym problemem, który napotyka kinematyka, jest to, że każde ciało ma pewną wielkość. Załóżmy, że musisz opisać ruch obiektu. Oznacza to uczenie się oznaczania swojej pozycji w dowolnym momencie. Ale każdy obiekt zajmuje pewną przestrzeń w przestrzeni. Oznacza to, że wszystkie części tego obiektu zajmują w tym samym czasie inne położenie.

W jakim przypadku należy opisać położenie całego obiektu? Jeśli weźmiesz pod uwagę każdy, obliczenia będą zbyt skomplikowane. Dlatego odpowiedź na to pytanie może być tak prosta, jak to tylko możliwe. Jeśli wszystkie punkty jednego ciała poruszają się w tym samym kierunku, to ten, który zawiera to ciało, wystarcza do opisania ruchu.

Rodzaje ruchu w kinematykach

Istnieją trzy rodzaje:

1. Progresywny to ruch, w którym każda linia prosta utrzymywana w ciele pozostaje równoległa do siebie. Na przykład samochód poruszający się po autostradzie powoduje taki ruch.
2. Obrót jest ruchem ciała, w którym wszystkie jego punkty poruszają się w kółko ze środkami leżącymi na jednej prostej, zwanej osią obrotu. Na przykład obrót Ziemi względem jej osi.
3. Oscylacyjne to ruch, w którym ciało powtarza swoją trajektorię po pewnym czasie. Na przykład ruch wahadła.

Podstawowe pojęcia kinematyki - punkt materialny

Każdy złożony ruch można opisać jako połączenie dwóch najprostszych typów - translacyjnego i rotacyjnego. Na przykład koło samochodu lub whirligig stojące na platformie poruszającej się prosto, są jednocześnie zaangażowane w te dwa rodzaje ruchu.

Ale co zrobić, jeśli ruch ciała nie może być przedstawiony jako kombinacja? Na przykład, jeśli samochód jedzie po wyboistej drodze, jego pozycja zmieni się w bardzo skomplikowany sposób. Jeśli liczyć tylko na to, że ten transport przemieszcza się z jednego miasta do drugiego, to w takiej sytuacji nie ma znaczenia, jaki rozmiar ciała przemieszcza się z punktu A do punktu B i może być zaniedbany. W takim przypadku ważne jest tylko to, jak długo samochód przejechał pewną odległość i przy jakiej prędkości się poruszał.

Należy jednak pamiętać, że lekceważenie rozmiaru nie jest dozwolone w każdym zadaniu. Na przykład, jeśli policzysz ruch podczas parkowania samochodu, ignorowanie jego wartości spowoduje katastrofalny efekt. Dlatego tylko w tych sytuacjach, w których w ramach określonego zadania można pominąć wymiary poruszającego się obiektu, wówczas taki obiekt nazywany jest zwykle punktem materialnym.

Wzory kinematyczne

Numery, za pomocą których określona jest pozycja punktu w przestrzeni, są nazywane współrzędnymi. Aby zdefiniować go na linii prostej, wystarczy jedna liczba, jeśli chodzi o powierzchnię, a następnie dwie, o przestrzeni - trzy. Więcej liczb w świecie trójwymiarowym (aby opisać położenie punktu materialnego) nie jest wymagane.

Istnieją trzy podstawowe równania dla koncepcji kinematyki, jako sekcja dotycząca ruchu ciał:

1. v = u + at.
2. S = ut + 1 / 2at ² .
3. v ² = u ² + 2as.

Gdzie

v = prędkość końcowa

u = prędkość początkowa,

a = przyspieszenie

s = odległość przebyta przez ciało

t = czas.

Formuły kinematyki w przestrzeni jednowymiarowej:

V = V _o + at

X - X _o = V _o t + 1 / 2a t2

V ² = V _o ¹ + 2a (X - X _o )

X - X _o = 12 (V _o + V) t
Gdzie

V - prędkość końcowa (m / s),

V _o - prędkość początkowa (m / s)

a - przyspieszenie (m / s ² ),

t - czas (czasy)

X jest końcową pozycją (m),

X ₀ - pozycja początkowa (m).

Wzory kinematyki w przestrzeni dwuwymiarowej

Ponieważ poniższe równania są używane do opisania punktu materialnego na płaszczyźnie, należy wziąć pod uwagę oś X i Y.

Biorąc pod uwagę kierunek X:

a _x = stała

V _fx = V _i x + a _x Δt

X _f = X _i + V _i x Δt + 1 / 2a _x Δt ²

Δt = V _fx -V _ix / a _x

V _fx ² = V _ix ² + 2ax Δx

X _f = X _i + 1/2 (V _fx + V _ix ) Δ t.
I biorąc pod uwagę kierunek y:

a _y = stała

V _fy = V _iy + a _y Δt

y _f = y _i + V _iy Δt + 1/2 a _x Δt ²

Δt = V _fy - V _iy / _ay

V _fy ² = V _iy ² + 2 _ay Δ _y

y _f = y _i +1/2 (V _fy + V _iy ) Δt.

Gdzie

V _f - prędkość końcowa (m / s),

V _i - prędkość początkowa (m / s)

a - przyspieszenie (m / s ² ),

t - czas (czasy)

X jest końcową pozycją (m),

X ₀ - pozycja początkowa (m).

Przenoszenie opuszczonego pocisku jest najlepszym przykładem opisującym ruch obiektu w dwóch wymiarach. Tutaj ciało porusza się, zarówno w pozycji pionowej Y, jak iw pozycji poziomej X, dlatego można powiedzieć, że obiekt ma dwie prędkości.

Przykłady problemów z kinematyką

Zadanie 1 : Początkowa prędkość wózka wynosi zero. Początkowo obiekt ten znajduje się w stanie spoczynku. Równomierne przyspieszenie zaczyna działać na nim w przedziale czasowym 5,21 sekundy. Odległość pokonywana przez ciężarówkę wynosi 110 m. Znajdź przyspieszenie.

Rozwiązanie:
Pokonana odległość wynosi s = 110 m,
prędkość początkowa v _i = 0,
czas t = 5,21 s
przyspieszenie a =?
Korzystając z podstawowej koncepcji i formuł kinematyki, możemy wywnioskować, że
s = v _i t + 1/2 przy ² ,
110 m = (0) × (5.21) + 1/2 × a (5.21) ² ,
a = 8,10 m / s ² .

Zadanie 2: Punkt porusza się wzdłuż osi x (w cm), po t sekundach podróży, można go przedstawić za pomocą równania x = 14t ² - t + 10. Konieczne jest znalezienie średnia prędkość punktów, pod warunkiem, że t = 3s?

Rozwiązanie:
Położenie punktu w t = 0 wynosi x = 10 cm.
Gdy t = 3s, x = 133 cm.
Średnia prędkość, V _av = Δx / Δt = 133-10 / 3-0 = 41 cm / s.

Co to jest odniesienie

O ruchu można mówić tylko wtedy, gdy jest coś, co uwzględnia zmianę pozycji badanego obiektu. Taki obiekt nazywany jest zbiorem odniesienia i zawsze warunkowo traktuje się go jako nieruchomy.

Jeśli zadanie nie wskazuje, w którym systemie raportu się porusza punkt materialny wtedy odniesieniem jest domyślnie ziemia. Jednakże nie oznacza to, że obiekt, który porusza się w stosunku do stacjonarnego w danym czasie, nie może być traktowany jak dowolny inny wygodny do obliczenia. Na przykład pociąg jadący, który zamienia samochód i tak dalej, może być traktowany jako odniesienie.

Układ odniesienia i jego wartość w kinemacie

Do opisu ruchu potrzebne są trzy elementy:

1. System współrzędnych
2. Ciało odniesienia.
3. Urządzenie do pomiaru czasu.

Ciało odniesienia, związany z nim układ współrzędnych i urządzenie do pomiaru czasu tworzą układ odniesienia. Nie ma sensu mówić o ruchu, jeśli nie jest to wskazane. Odpowiednio dobrany układ odniesienia pozwala uprościć opis przemieszczenia i odwrotnie, komplikuje go, jeśli jest źle dobrany.

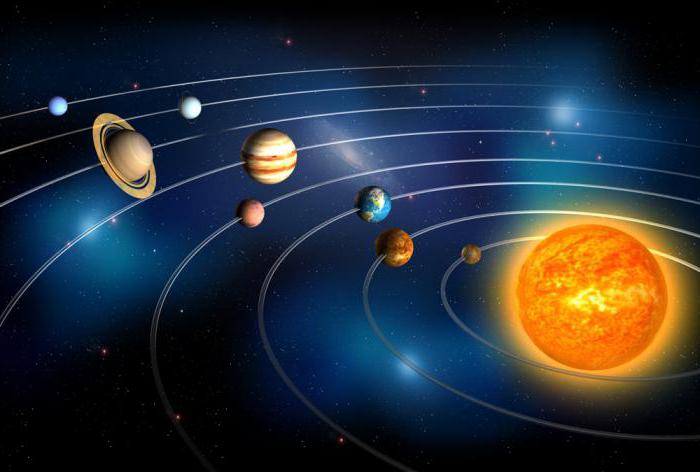
Z tego powodu ludzkość od dawna wierzyła, że ​​słońce porusza się wokół Ziemi i że znajduje się w centrum wszechświata. Taki złożony ruch gwiazd, ze względu na to, że ziemscy obserwatorzy znajdują się w układzie odniesienia, który jest bardzo misternie poruszający. Ziemia obraca się wokół własnej osi i jednocześnie wokół Słońca. W rzeczywistości, jeśli zmienisz system odniesienia, wówczas wszystkie ruchy ciał niebieskich będą łatwe do opisania. To było kiedyś zrobione przez Kopernika. Zaproponował własny opis porządku światowego, w którym słońce jest w bezruchu. Jeśli chodzi o to, o wiele łatwiej jest opisać ruch planet niż gdyby Ziemia była odniesieniem.

Podstawowe pojęcia kinematyki - ścieżka i trajektoria

Niech jakiś punkt po raz pierwszy znajduje się w pozycji A, po pewnym czasie znalazł się w pozycji B. Między nimi możesz narysować jedną linię. Ale aby ta prosta linia zawierała więcej informacji o ruchu, to znaczy, było jasne, gdzie i gdzie poruszało się ciało, nie może to być tylko odcinek, ale skierowany, zwykle oznaczony literą S. Poprzez ruch ciała, nazywany jest wektorem zaczerpniętym z początkowej pozycji obiektu w finał.

Jeśli ciało pierwotnie znajdowało się w punkcie A, a następnie okazało się, że znajduje się w punkcie B, nie oznacza to, że poruszało się tylko w linii prostej. Z jednej pozycji do drugiej można dotrzeć na nieskończenie wiele sposobów. Linia, wzdłuż której porusza się ciało, to kolejna podstawowa koncepcja kinematyki - trajektoria. A jego długość nazywana jest ścieżką, którą zwykle oznaczają litery L lub l.