Impuls ciała: definicja i właściwości

W życiu codziennym epitet "impulsywny" jest czasem używany do scharakteryzowania osoby dokonującej aktów spontanicznych. Jednak niektórzy ludzie nawet nie pamiętają, a znaczna część nie wie nawet, z jaką ilością fizyczną powiązane jest to słowo. Co kryje się pod pojęciem "impulsu ciała" i jakie ma właściwości? Odpowiedzi na te pytania poszukiwali tak wielcy naukowcy, jak Rene Descartes i Isaac Newton.

Impuls ciała: definicja

Jak każda nauka, fizyka działa z jasno zdefiniowanymi pojęciami. W chwili obecnej przyjęto następującą definicję dla ilości z nazwą impulsu ciała: jest to wielkość wektorowa, która jest miarą (ilością) mechanicznego ruchu ciała.

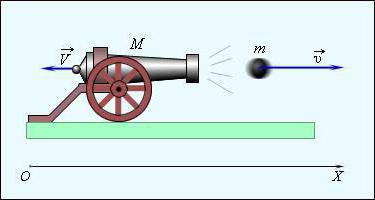
Załóżmy, że pytanie rozważane jest w ramach mechaniki klasycznej, to znaczy, że uważa się, że ciało porusza się z prędkością normalną, a nie relatywistyczną, co oznacza, że ​​jest co najmniej rzędu wielkości mniejszej niż prędkość światła w próżni. Następnie moduł impulsu ciała oblicza się za pomocą wzoru 1 (patrz zdjęcie poniżej).

Tak więc, z definicji, ta wartość jest równa iloczynowi masy ciała i jego prędkości, z którą jego wektor jest współkierowany.

Jednostką pomiaru impulsu w SI (Międzynarodowy System Jednostek) przyjmuje się 1 kg / m / s.

Skąd pochodzi określenie "impuls"?

Kilka wieków przed pojawieniem się pojęcia ilości w fizyce ruch mechaniczny ciała, uważano, że przyczyną jakiegokolwiek ruchu w przestrzeni jest specjalna siła - impeus.

W XIV wieku Jean Buridan wprowadził poprawki do tej koncepcji. Zasugerował, że latający bruk ma impet proporcjonalny wprost do prędkości, który pozostałby niezmieniony, gdyby nie było oporu powietrza. Jednocześnie, w opinii tego filozofa, ciała o większej wadze miały zdolność "powstrzymywania" większej części takiej siły napędowej.

Dalszy rozwój koncepcji, nazwany później impulsem, dał Rene Descartes, który wyznaczył ją słowami "ilość ruchu". Nie wziął jednak pod uwagę, że prędkość ma kierunek. Dlatego teoria przedstawiona przez niego w niektórych przypadkach zaprzeczyła doświadczeniu i nie znalazła uznania.

Fakt, że ruch musi mieć kierunek, został po raz pierwszy odgadnięty przez angielskiego naukowca Johna Wallisa. Stało się to w 1668 roku. Jednak zajęło mu to kolejne kilka lat sformułowanie słynnego prawa zachowania pędu. Dowód teoretyczny tego faktu, ustalony empirycznie, został podany przez Izaaka Newtona, który posłużył się trzecim i drugim prawem odkrytej przez niego mechaniki klasycznej, nazwanej jego imieniem.

Impuls systemu punktów materialnych

Zastanów się najpierw, jeśli chodzi o prędkości, które są znacznie niższe niż prędkość światła. Następnie, zgodnie z prawami mechaniki klasycznej, całkowity impuls systemu istotne punkty reprezentuje ilość wektorową. Jest równa sumie produktów ich mas z prędkością (patrz wzór 2 na powyższym obrazku).

W tym samym czasie, dla impulsu jednego punktu materialnego, przyjmują one wielkość wektora (wzór 3), który jest współkierowany z prędkością cząstki.

Jeśli mówimy o ciele o skończonej wielkości, to najpierw zostaje on rozbity umysłowo na małe części. W ten sposób ponownie rozpatruje się system punktów materialnych, jednak jego pęd oblicza się nie poprzez zwykłe sumowanie, lecz poprzez integrację (patrz wzór 4).

Jak widzimy, nie ma zależności czasowej, dlatego impuls systemu, na który nie działają siły zewnętrzne (lub ich wpływ jest wzajemnie kompensowany), pozostaje niezmieniony w czasie.

Dowód prawa ochrony

Nadal uważamy ciało o skończonej wielkości za system punktów materialnych. Dla każdego z nich drugie prawo Newtona sformułowano zgodnie ze wzorem 5.

Zwróć uwagę na to, że system jest zamknięty. Następnie, podsumowując wszystkie punkty i stosując trzecie prawo Newtona, uzyskujemy wyrażenie 6.

Tak więc pęd systemu zamkniętego jest stały.

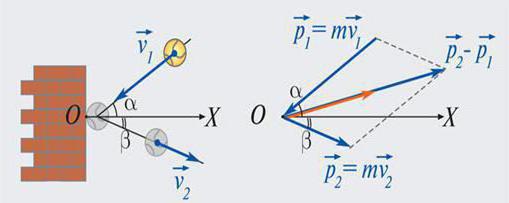
Prawo zachowania jest również ważne w przypadkach, gdy całkowita suma sił działających na układ z zewnątrz wynosi zero. Stąd wynika jedno ważne, konkretne stwierdzenie. Stwierdza, że ​​impuls ciała jest stały, jeśli nie ma wpływu zewnętrznego, lub wpływ kilku sił jest kompensowany. Na przykład, przy braku tarcia po uderzeniu kijem, krążek musi utrzymać swój pęd. Sytuacja ta będzie widoczna nawet wtedy, gdy dotknie to ciało grawitacja i reakcje wspomagające (lód), ponieważ chociaż są one równe co do wielkości, są skierowane w przeciwnych kierunkach, tj. kompensują się nawzajem.

Właściwości

Impuls ciała lub punktu materialnego jest ilością addytywną. Co to znaczy? Wszystko jest proste: impuls układu mechanicznego punktów materialnych składa się z impulsów wszystkich punktów materialnych zawartych w systemie.

Drugą właściwością tej ilości jest to, że pozostaje ona niezmieniona podczas interakcji, które zmieniają jedynie charakterystykę mechaniczną układu.

Ponadto impuls jest niezmienny w stosunku do dowolnej rotacji układu odniesienia.

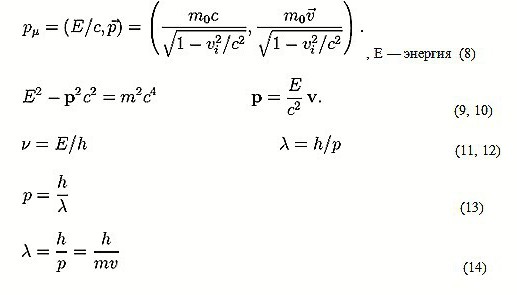
Relatywistyczny przypadek

Załóżmy, że mówimy o nieodtwarzaniu punktów materialnych o prędkości rzędu 10 do 8 mocy lub nieco mniej w systemie SI. Trójwymiarowy impuls oblicza się za pomocą wzoru 7, gdzie przez c mamy na myśli prędkość światła w próżni.

W przypadku, gdy jest ona zamknięta, prawo zachowania pędu jest prawdziwe. Jednocześnie, pęd trójwymiarowy nie jest relatywistyczną niezmienną wielkością, ponieważ istnieje zależność od układu odniesienia. Istnieje również opcja czterowymiarowa. Dla jednego punktu materialnego określa go wzór 8.

Impuls i energia

Ilości te, jak również masa, są ściśle ze sobą powiązane. W praktycznych problemach zwykle stosuje się relacje (9) i (10).

Ustalenie za pomocą fal de Broglie

W 1924 r. Wysunięto hipotezę, że nie tylko fotony, ale także wszelkie inne cząstki (protony, elektrony, atomy) mają dualność falowo-cząsteczkową. Jego autorem był francuski naukowiec Louis de Broglie. Jeśli przełożymy tę hipotezę na język matematyki, można argumentować, że każda cząstka z energią i pędem jest związana z falą o częstotliwości i długości wyrażonej odpowiednio przez wzory 11 i 12 (h jest stałą Plancka).

Z ostatniej relacji wynika, że ​​moduł impulsu i długość fali, oznaczona literą "lambda", są odwrotnie proporcjonalne do siebie (13).

Jeżeli rozważa się cząstkę o stosunkowo niskiej energii, która porusza się z prędkością niewspółmierną do prędkości światła, wówczas moduł impulsowy oblicza się w taki sam sposób, jak w mechanice klasycznej (patrz wzór 1). W konsekwencji długość fali jest obliczana zgodnie z wyrażeniem 14. Innymi słowy, jest odwrotnie proporcjonalna do iloczynu masy i prędkości cząstki, to znaczy do jej pędu.

Teraz wiesz, że impuls ciała jest miarą mechanicznego ruchu, a ty poznałeś jego właściwości. Wśród nich, w praktyce, szczególnie ważne jest prawo zachowania. Nawet ludzie z dala od fizyki obserwują go w życiu codziennym. Na przykład, wszyscy wiemy, że broń palna i artyleria przekazują informacje zwrotne podczas strzelania. Prawo zachowania pędu wyraźnie pokazuje grę w bilard. Dzięki niemu możesz przewidzieć kierunek ekspansji piłek po uderzeniu.

Prawo znalazło zastosowanie w obliczeniach niezbędnych do zbadania skutków możliwych wybuchów, w zakresie tworzenia aparatu odrzutowego, w projektowaniu broni palnej i w wielu innych dziedzinach życia.