Wyrażenie logiczne: buduj i upraszczaj

Głównym zadaniem logiki jest sprawdzenie, czy stwierdzenie jest fałszywe, czy też może być uznane za prawdziwe. W tym celu wynaleziono kilka metod. Opracowane sposoby określania prawda jest lub fałszywe, oparte na innych wypowiedziach i ich atrybutach. Wyrażenie logiczne - baza koncepcja nauki a jego parametry określają, które operacje można wykonać.

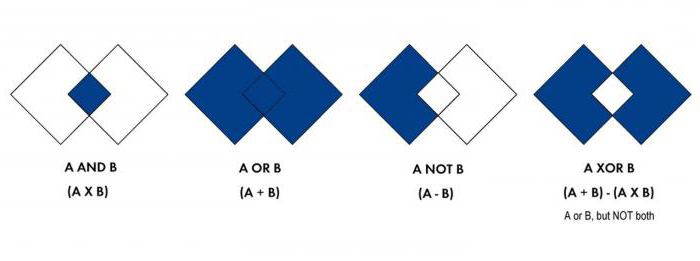
Ogólne warunki

Dziś logika jest badana w formie logiki matematycznej. Opiera się wyłącznie na formalnych metodach poznania. Jedną z kluczowych części tego kierunku jest algebra logiki. Specjalizuje się tylko w złożonych obiektach i metodach, które pozwalają na ustawienie ich parametrów. Używał ściśle algebraicznych sposobów uczenia się.

Nauka nazywa się algebrą Boole'a, ponieważ jej autorem jest George Boole, sformułował swoje główne idee w 1854 roku, kiedy opublikował podstawową książkę. Boule postawił sobie zadanie zbadania operacji, na podstawie których funkcjonuje ludzki umysł, zrozumienia mechanizmu rozumowania, opisania go symbolami. Po osiągnięciu tego sukcesu udało mu się stworzyć nową naukę.

Wyrażenia logiczne w programowaniu

Warunkowe wyrażenie logiczne to niektóre zmienne i stałe, które są klasyfikowane jako proste. Wszystkie obiekty są łączone ze sobą przez porównanie. . W wyniku obliczeń możliwe jest uzyskanie skończonego wyrażenia warunkowego: prawda lub fałsz .

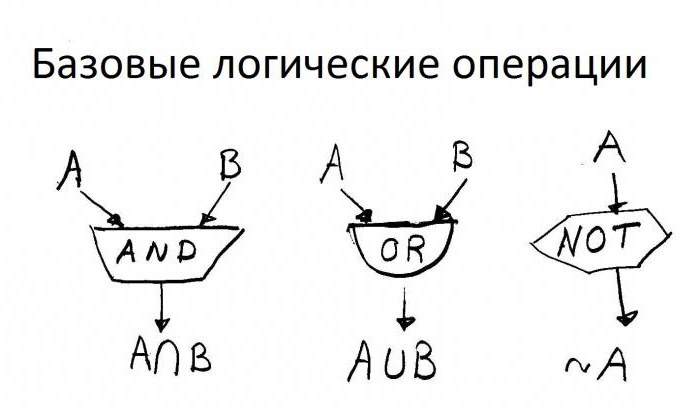
Najbardziej stosowna logika w programowaniu. Na przykładzie Pascala możemy wyróżnić najważniejsze operacje stosowane w praktyce:

• definicja większego z nich;
• definicja mniejszego z nich;
• obliczanie mniejszej lub równej;
• obliczenie większe lub równe;
• definicja równości dwóch wyrażeń;
• wniosek, że wyrażenia nie są równe.

Jeśli podczas programowania konieczne jest skonstruowanie wyrażenia logicznego, ale liczby rzeczywiste są porównywane ze sobą, należy wziąć pod uwagę następujący fakt: reprezentacja liczb jest niedokładna, ponieważ konieczne jest zaokrąglenie. Oznacza to, że działanie obliczania ścisłej równości nie może być dokładne. Doświadczeni programiści zalecają, w miarę możliwości, unikanie dostępu do tej operacji, ponieważ jest prawdopodobne, że równość zostanie ostatecznie uznana za fałszywą, bez bycia taką.

Przykład: x = (2,23 * x / 2,23)

Zgadzam się, prawda o formule jest widoczna wizualnie. Ale podczas zapisywania go w kodzie komputerowym i nieuchronności błędu zaokrąglania w obliczeniach, będzie to fałsz.

Kolejny subtelny punkt: warunkowe wyrażenie logiczne jest koniecznie zapisane w nawiasach, jeśli jest operandem. Zasada wynika z opracowanej hierarchii operacji. Na przykład porównanie w jego priorytecie jest niższe niż inne, a operacje logiczne są wysokie. . Aby zmienić proces obliczania konkretnego przykładu w odniesieniu do takiego zamówienia, konieczne jest umieszczenie nawiasów .

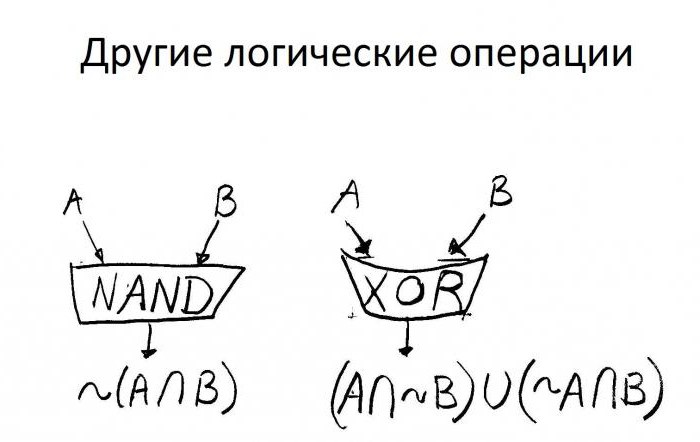
Podstawy nauki

Obiekt w logice jest powszechnie rozumiany jako narracja, która jest dokładnie opisana jako kłamstwo, prawda. Wartość wyrażenia logicznego, jeśli jest prawdziwa, jest zapisywana jako jedna, druga opcja jest oznaczana jako zero.

W operacjach logicznych powszechnie rozumie się takie działania (z reguły proces myślenia), które ostatecznie dają wzrost wiedzy, a także prowadzą do tworzenia zupełnie nowych obiektów.

Wyrażenie logiczne jest ustne, możesz je zapisać. Jest on zawarty w obiektach wraz ze stałymi. Wyrażenie bezpośrednio zależy od zmiennych obiektów, stając się jednym lub zerem.

Jeśli miałbyś do czynienia ze złożoną instrukcją, musisz pamiętać, że zawiera ona złożone, proste wyrażenia, do których połączeń użyto logiczne operacje.

Logika identyfikuje kluczowe operacje zwane:

• koniunkcja;
• równoważność;
• alternatywa;
• implikacja;
• inwersja

. Aby rozwiązać prawie każdy ich przykład wystarczy .

Połączenie

Termin ten jest powszechnie rozumiany jako tak złożona operacja, która może być prawdziwa tylko wtedy, gdy oba proste składniki są prawdziwe. Inne opcje są uznawane za fałszywe.

Jest napisany jako: F = A i B.

Tabela:

Disjunction

W tej sytuacji prawda wyrażeń logicznych jest określana na podstawie analizy wartości (jednego i zera) składowych prostych wyrażeń. Jeśli oba są fałszywe, funkcja ma także wartość zero. W przeciwnym razie jego wartość wynosi jeden.

Jest napisany jako: F = A + B.

Tabela:

Inwersja

Termin odnosi się do operacji, kiedy zamienia się w fałszywe wyrażenie, które wcześniej było prawdziwe i na odwrót. Jeśli obiekt źródłowy jest poprawny, wynik jest fałszywy i jeśli początkowo było kłamstwem, przekształca się w prawdę.

Tabela:

Równoważność

To logiczne wyrażenie będzie oznaczało tylko jedno, gdy oba wyrażenia w tym przykładzie oznaczają to samo.

Tabela:

Implikacja

Termin ten stosuje się do takiego złożonego wyrażenia logiki, które jest fałszywe, jeśli fałszywe wynika z prawdy. Inne sytuacje: wartość równa się jeden. Operacja jest stosowana do dwóch prostych obiektów, z których jeden nazywa się warunkiem, a drugi jest konsekwencją.

Tabela:

Operacje: niuanse logiczne

Wiedząc, jakie wyrażenie logiczne jest używane jako obiekt, można poprawnie obliczyć wynik. Jednocześnie należy pamiętać, że operacje logiczne są tak arytmetyczne jak operacje niezbędne do interakcji z liczbami. . Operacje logiczne pomagają budować wyrażenia logiczne - jest to również paralelą z algebrą .

W ramach wyrażeń logicznych są to stałe i zmienne. Pierwszy ma określoną wartość - zero lub jeden. Jeśli wyrażenie zawiera pewne zmienne, ustawi w ten sposób funkcję boolowską, której wartość jest obliczana na podstawie argumentów. Wartości argumentów dla każdego zadania są określone w warunkach. Trzeba tylko zastąpić je wyrażeniem, a następnie przeprowadzić dalsze obliczenia.

Każde wyrażenie logiczne może mieć swoją własną tabelę prawdy, to jest obiekt, który szczegółowo opisuje wszystkie warianty, które wartości i kiedy funkcja akceptuje, jeśli używany jest określony zestaw zmiennych. Jedna linia takiej tabeli to jeden zestaw warunków początkowych do obliczeń. . Jeśli N zmiennych jest zaangażowanych w tę funkcję, wówczas jest dwa razy więcej linii .

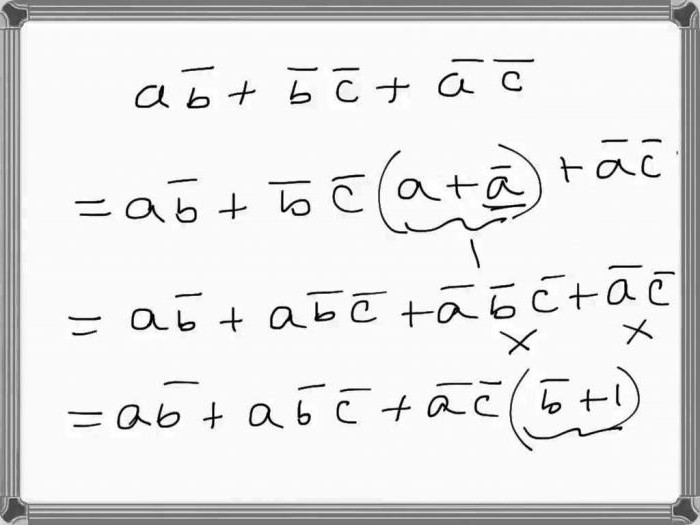
Tabele prawdy

Istnieją następujące ogólne właściwości charakterystyczne dla każdej tabeli:

• liczba wspomnianych linii, dwukrotność liczby zmiennych;
• Liczba kolumn w tabeli to o jeden więcej niż liczba zmiennych.

Bez względu na to, jaki zestaw wartości zmiennych jest podany w warunku, zawsze można sformułować wyrażenie, które będzie równe jedności na pewnym zestawie zmiennych.

Jest rejestrowane jako "odłączenie koniunkcji". W praktyce oznacza to, że możesz zbudować określoną ekspresję, mając przed sobą gotowy stół prawdy. Oczywiście objętość tej tabeli może znacznie skomplikować zadanie matematyki.

Uprość

Często zdarzają się sytuacje, w których wyrażenie matematyczne wymaga uproszczenia dla adekwatności rozwiązania. Istnieją pewne konwersje, które mają zastosowanie w logice Boole'a.

W szczególności jedno wyrażenie można zastąpić innym, które jest równoważne. Sprawdź równoważność, analizując tabele prawdy. Jeśli pasują, możesz wymienić. . Tutaj zaczyna obowiązywać fałszywa zasada, gdy w obiekcie A jest ona zamieniona na pewne podwyrażenie P, które było obecne tutaj przed Q, i uzyskano wyrażenie B. We wszystkich obliczeniach jest ono równoważne A.

Uproszczenie wyrażeń logicznych nazywa się zwykle minimalizacją. Głównym zadaniem minimalizacji jest reprezentowanie funkcji w takiej formie, gdy litery, operacje, jest najmniejszą możliwą liczbą. Możesz osiągnąć pożądaną jedną z dwóch opcji:

• algebraiczny;
• grafika.

Metoda algebraiczna

Wyrażenie logiczne można uprościć metodą algebraiczną, upraszczając formułę. Odbywa się to poprzez równoważne przekształcenia opisane powyżej. Konieczne jest uwzględnienie tożsamości i reguł istniejących w algebrze Boole'a.

Uproszczone wyrażenie od tego, które początkowo trzeba było rozwiązać, różni się przede wszystkim liczbą liter. Jednak często występują problemy, gdy trzeba udowodnić równoważność pierwotnego wyrażenia i wynikającego z niego uproszczenia. Odbywa się to poprzez porównanie tabel prawdy.

Jeśli przykład przedstawia elementarne stwierdzenia, można dokonać ich modyfikacji, odwołując się nie tylko do ogólnych zasad, ale także do tych związanych z operacjami na zestawach.

Podczas analizowania instrukcji związanych z zestawami często najlepszą opcją jest redukcja wyrażeń do implikacji, gdy członkowie nie zawierają już implikacji.