Przyspieszenie dośrodkowe - formuła wyjściowa i praktyczne zastosowanie

Przyspieszenie dośrodkowe towarzyszy nam wszędzie. To sprawia, że ​​nasze Ziemia obraca się wokół Słońca. Powstała grawitacja pozwala nam istnieć na tej planecie. Jak można zrozumieć, jakie jest przyspieszenie dośrodkowe? Definicję tej wielkości fizycznej przedstawiono poniżej.

Obserwacje

Najprostszy przykład przyspieszenia poruszającego się w kółku ciała można zaobserwować obracając kamień na linie. Ciągniesz za linę, a lina ciągnie kamień do środka. W każdym momencie lina przekazuje kamień pewną ilość ruchu i za każdym razem - w nowym kierunku. Możesz sobie wyobrazić ruch liny w postaci serii słabych szarpnięć. Szarpnięcie - i lina zmienia kierunek, kolejne szarpnięcie - kolejna zmiana, i tak dalej w kółko. Jeśli nagle uwolnisz linę, szarpnięcia zatrzymają się, a wraz z nimi zmiana kierunku prędkości zatrzyma się. Kamień przesunie się w kierunku stycznej do okręgu. Powstaje pytanie: "Z jakim przyspieszeniem ciało porusza się w tej chwili?"

Formuła przyspieszenia dośrodkowego

Przede wszystkim warto zauważyć, że ruch ciała w kole jest trudny. Kamień uczestniczy jednocześnie w dwóch rodzajach ruchu: pod działaniem siły porusza się w kierunku środka obrotu, a jednocześnie stycznie do okręgu, oddala się od tego środka. Zgodnie z drugim prawem Newtona siła trzymająca kamień na linie jest skierowana w kierunku środka obrotu wzdłuż tej liny. Zostanie również skierowany do wektora przyspieszenia.

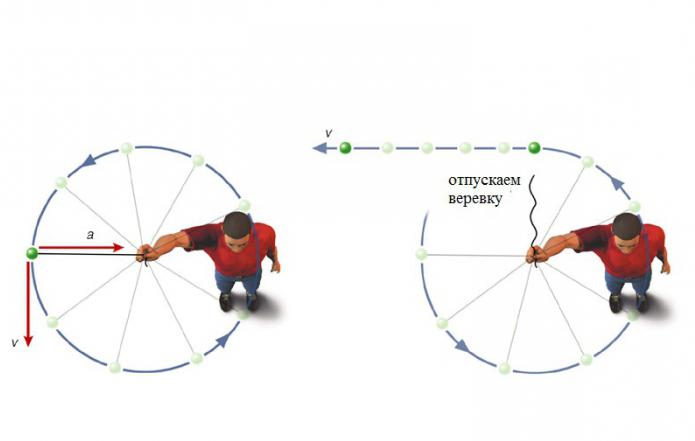
Niech przez jakiś czas nasz kamień, poruszający się jednostajnie z prędkością V, dostaje się z punktu A do punktu B. Przypuśćmy, że w chwili, gdy ciało przekroczy punkt B, siła dośrodkowa przestaje na nim działać. Potem przez pewien czas spadałby w punkcie K. Leży na stycznej. Gdyby w tym samym momencie oddziaływały na ciało tylko siły dośrodkowe, to w czasie t, poruszającym się z tym samym przyspieszeniem, pojawiłoby się ono w punkcie O, który znajduje się na linii prostej, która reprezentuje średnicę koła. Oba segmenty są wektorami i przestrzegają zasady dodawania wektorów. W wyniku sumowania tych dwóch ruchów w przedziale czasowym t uzyskamy wynikowy ruch wzdłuż łuku AB.

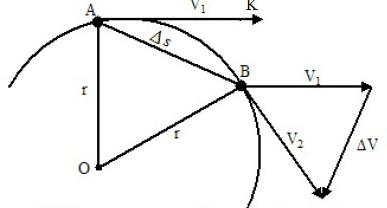
Jeśli przedział czasowy t zostanie uznany za nieistotny, wówczas łuk AB będzie się nieznacznie różnić od akordu AB. W ten sposób możliwe jest zastąpienie ruchu wzdłuż łuku ruchem wzdłuż cięciwy. W takim przypadku ruch kamienia wzdłuż cięciwy będzie zgodny z prawami ruchu prostoliniowego, to znaczy odległość przebyta AB będzie równa iloczynowi prędkości kamienia w momencie jego ruchu. AB = V x t.

Oznacz pożądane przyspieszenie dośrodkowe według litery a. Następnie ścieżkę pokrytą tylko działaniem przyspieszenia dośrodkowego można obliczyć za pomocą formuły ruchu przyspieszonego równomiernie:

AO = przy 2/2.

Odległość AB jest równa iloczynowi prędkości i czasu, czyli AB = V x t,

AO - poprzednio obliczone przez formułę ruch równomiernie przyspieszony poruszać się po linii prostej: AO = przy 2/2.

Zastępując te dane formułą i przekształcając ją otrzymujemy prostą i elegancką formułę przyspieszenia dośrodkowego:

a = v ² / R

Można to wyrazić słowami w następujący sposób: przyspieszenie dośrodkowe ciała poruszającego się w okręgu jest równe ilorazowi z dzielenia prędkości liniowej podniesionej do kwadratu o promień koła, w którym obraca się ciało. Siła dośrodkowa w tym przypadku będzie wyglądać jak obraz poniżej.

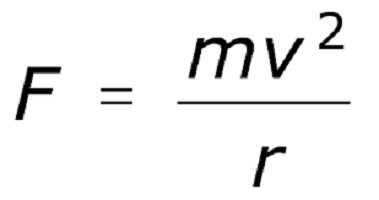
Prędkość kątowa

Prędkość kątowa równy ilorazowi prędkości liniowej podzielonej przez promień koła. Odwrotność jest również prawdziwa: V = ωR, gdzie ω jest prędkością kątową

Jeśli zastąpisz tę wartość we wzorze, możesz uzyskać wyrażenie przyspieszenia odśrodkowego dla prędkości kątowej. Będzie wyglądać tak:

a = ω ² R.

Przyspieszenie bez zmiany prędkości

A jednak, dlaczego ciało z przyspieszeniem skierowanym w stronę środka nie porusza się szybciej i nie zbliża się do środka obrotu? Odpowiedź leży w samym sformułowaniu przyspieszenia. Fakty sugerują, że jazda w kole jest prawdziwa, ale aby ją utrzymać, wymagane jest przyspieszenie skierowane do środka. Pod działaniem siły wywołanej przez to przyspieszenie następuje zmiana w ilości ruchu, w wyniku której trajektoria ruchu stale się wygina, cały czas zmieniając kierunek wektora prędkości, ale nie zmieniając jego wartości bezwzględnej. Krążąc w kółko, nasz cierpiący kamień pędzi do wewnątrz, w przeciwnym razie będzie poruszał się po stycznej. Każda chwila czasu, pozostawiając na stycznej, kamień przyciąga do środka, ale nie wpada w niego. Innym przykładem przyspieszenia dośrodkowego może być narciarz wodny, opisujący małe kółka na wodzie. Postać sportowca jest przechylona; wydaje się, że upada, nadal się poruszając i pochylając się do przodu.

Tak więc możemy stwierdzić, że przyspieszenie nie zwiększa prędkości ciała, ponieważ wektory prędkości i przyspieszenia są prostopadłe do siebie. Dodając do wektora prędkości, przyspieszenie zmienia jedynie kierunek ruchu i utrzymuje ciało na orbicie.

Nadmiar marginesu bezpieczeństwa

W poprzednim doświadczeniu mieliśmy do czynienia z idealną liną, która nie była rozdarta. Ale, powiedzmy, nasza lina jest najczęstsza, a ty możesz nawet obliczyć siłę, po której po prostu się złamie. Aby obliczyć tę siłę, wystarczy porównać margines bezpieczeństwa liny z obciążeniem, którego doświadcza w procesie obrotu kamienia. Obracając kamień z większą prędkością, dajesz mu większy ruch, co oznacza większe przyspieszenie.

Przy średnicy liny jutowej około 20 mm wytrzymałość na rozciąganie wynosi około 26 kN. Warto zauważyć, że długość liny nie pojawia się nigdzie. Obracając ładunek o wielkości 1 kg na linie o promieniu 1 m, można obliczyć, że prędkość liniowa wymagana do jej złamania wynosi 26 x 10 ³ = 1 kg x V 2/1 m. Dlatego prędkość, która jest niebezpieczna do przekroczenia jest równa √ 26 x 10 ³ = 161 m / s.

Grawitacja

Rozważając to doświadczenie, zaniedbaliśmy działanie grawitacja ponieważ przy tak dużych prędkościach jego wpływ jest znikomy. Ale można zauważyć, że podczas rozwijania długiej liny ciało opisuje bardziej złożoną trajektorię i stopniowo zbliża się do ziemi.

Niebiańskie ciała

Jeśli przeniesiemy prawa ruchu wzdłuż koła do przestrzeni i zastosujemy je do ruchu ciał niebieskich Możesz ponownie otworzyć kilka znanych formuł. Na przykład siła, z jaką ciało jest przyciągane do Ziemi, jest znana formułą:

F = m * g.

W naszym przypadku czynnik g to bardzo przyspieszenie dośrodkowe, które pochodzi z poprzedniej formuły. Tylko w tym przypadku rola kamienia zostanie wykonana przez ciało niebieskie, przyciągnięte do Ziemi, a rola liny - siła grawitacji. Mnożnik g będzie wyrażany przez promień naszej planety i prędkość jego rotacji.

Wyniki

Istota przyspieszenia dośrodkowego polega na ciężkiej i niewdzięcznej pracy utrzymywania poruszającego się ciała na orbicie. Istnieje paradoksalny przypadek, gdy przy stałym przyspieszeniu ciało nie zmienia wielkości jego prędkości. Dla niedoświadczonego umysłu takie stwierdzenie jest raczej paradoksalne. Niemniej jednak, przy obliczaniu ruchu elektronu wokół jądra i przy obliczaniu prędkości obrotowej gwiazdy wokół czarnej dziury, przyspieszenie dośrodkowe nie odgrywa roli ostatecznej.