Współczynnik korelacji i związek przyczynowy: formuły i ich interpretacja

Współczynnik korelacji to stopień połączenia między dwiema zmiennymi. Jego obliczenia dają wyobrażenie, czy istnieje zależność między dwoma macierzami danych. W przeciwieństwie do regresji korelacja nie pozwala na przewidywanie wartości ilości. Jednak obliczenie współczynnika jest ważnym etapem wstępnej analizy statystycznej. Na przykład stwierdziliśmy, że współczynnik korelacji pomiędzy poziomem bezpośrednich inwestycji zagranicznych a tempem wzrostu PKB jest wysoki. Daje nam to pogląd, że aby zapewnić dobrobyt, konieczne jest stworzenie sprzyjającego klimatu specjalnie dla zagranicznych przedsiębiorców. Nie taki oczywisty wniosek na pierwszy rzut oka!

Korelacja i przyczynowość

Być może nie ma jednego obszaru statystycznego, który byłby tak mocno ugruntowany w naszym życiu. Współczynnik korelacji stosowany jest we wszystkich obszarach wiedzy publicznej. Jego główne niebezpieczeństwo polega na tym, że jego wysokie wartości są często spekulowane, aby przekonać ludzi i przekonać ich do pewnych wniosków. W rzeczywistości jednak silna korelacja wcale nie wskazuje na związek przyczynowy między ilościami.

Współczynnik korelacji: formuła Pearsona i Spearmana

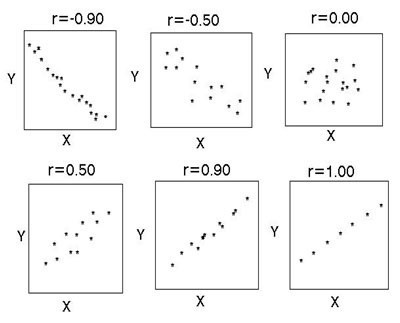
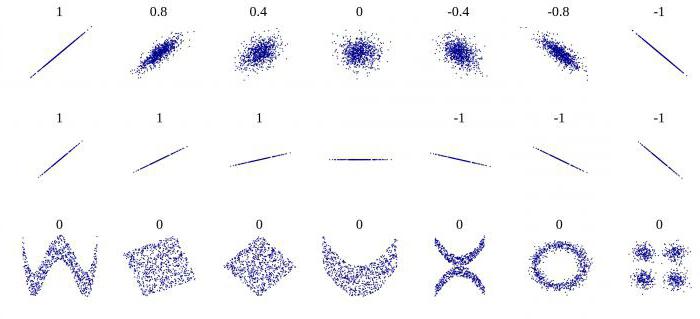
Istnieje kilka kluczowych wskaźników, które charakteryzują związek między dwiema zmiennymi. Historycznie pierwszy z nich to współczynnik korelacji liniowej Pearsona. Wciąż jest w szkole. Został opracowany przez C. Pearson i J. Yul na podstawie prac Fr. Galton. Współczynnik ten pozwala zobaczyć związek między liczbami wymiernymi, które zmieniają się racjonalnie. Jest zawsze większa niż -1 i mniejsza niż 1. Liczba ujemna wskazuje na zależność odwrotnie proporcjonalną. Jeśli współczynnik wynosi zero, wówczas nie ma połączenia między zmiennymi. Równy liczbie dodatniej - istnieje wprost proporcjonalna zależność między badanymi ilościami. Współczynnik korelacji rang Spearmana pozwala uprościć obliczenia, budując hierarchię wartości zmiennych.

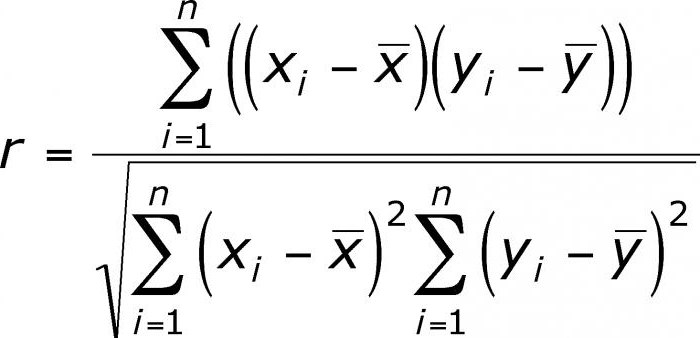
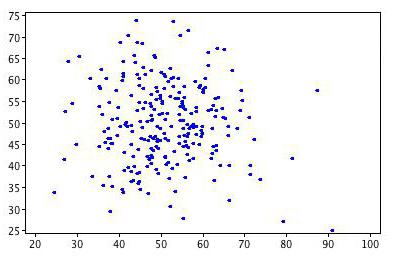
Związek między zmiennymi

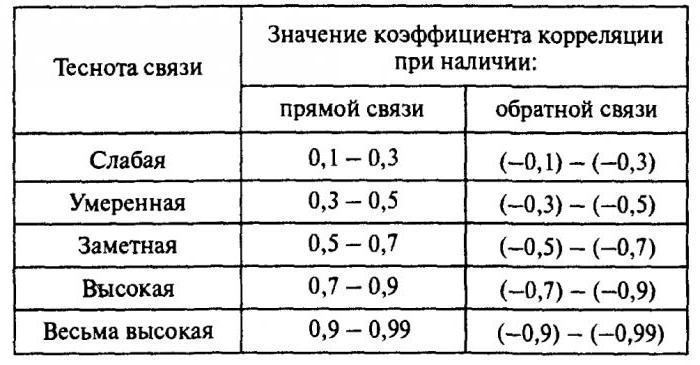
Korelacja pomaga znaleźć odpowiedź na dwa pytania. Po pierwsze, związek między zmiennymi dodatnimi lub ujemnymi. Po drugie, jak silne jest uzależnienie. Analiza korelacji to potężne narzędzie, dzięki któremu możesz uzyskać te ważne informacje. Łatwo zauważyć, że dochody i wydatki rodziny spadają i rosną proporcjonalnie. Ta relacja jest uważana za pozytywną. Wręcz przeciwnie, wraz ze wzrostem cen towarów spada popyt na nie. Takie połączenie nazywa się ujemnym. Wartości współczynnika korelacji mieszczą się w zakresie od -1 do 1. Zero oznacza, że ​​nie ma związku między badanymi wartościami. Im bliżej wskaźnika do skrajnych wartości, tym silniejsze połączenie (ujemne lub dodatnie). Brak zależności jest wskazywany przez współczynnik od -0,1 do 0,1. Trzeba zrozumieć, że taka wartość wskazuje tylko na brak połączenia liniowego.

Funkcje aplikacji

Korzystanie z obu wskaźników podlega pewnym założeniom. Po pierwsze, obecność silnego połączenia nie oznacza, że ​​jedna ilość determinuje inną. Może być trzecia ilość, która definiuje każdą z nich. Po drugie, wysoki współczynnik korelacji Pearsona nie wskazuje związku przyczynowego między badanymi zmiennymi. Po trzecie pokazuje tylko zależność liniową. Korelacji można użyć do oszacowania istotnych danych ilościowych (na przykład ciśnienia atmosferycznego, temperatury powietrza), a nie do kategorii takich jak płeć czy ulubiony kolor.

Wielokrotny współczynnik korelacji

Pearson i Spearman zbadali związek między tymi dwiema zmiennymi. Ale jak działać w przypadku, gdy są trzy lub nawet więcej. Tutaj na ratunek przychodzi wielokrotny współczynnik korelacji. Na przykład na produkt narodowy brutto wpływa nie tylko bezpośredni inwestycje zagraniczne ale także pieniężne i polityka fiskalna stan, a także poziom eksportu. Tempo wzrostu i wielkość PKB są wynikiem interakcji wielu czynników. Należy jednak rozumieć, że model wielokrotnej korelacji opiera się na szeregu uproszczeń i założeń. Po pierwsze, wieloliniowość pomiędzy ilościami jest wykluczona. Po drugie zakłada się, że zależność między zależnym i zmiennymi oddziałującymi na nie jest liniowa.

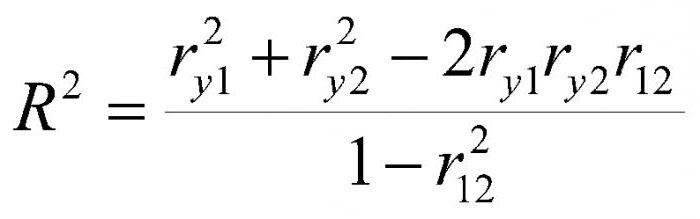
Obszary zastosowania analizy korelacji i regresji

Ta metoda znajdowania zależności między ilościami jest szeroko stosowana w statystykach. Najczęściej korzysta się z niego w trzech głównych przypadkach:

1. Aby przetestować przyczynową zależność między wartościami dwóch zmiennych. W rezultacie badacz ma nadzieję znaleźć liniową relację i wyprowadzić formułę opisującą te zależności między ilościami. Jednostki ich pomiarów mogą być inne.
2. Aby sprawdzić połączenie między wartościami. W tym przypadku nikt nie określa, która zmienna jest zależna. Może się okazać, że wartość obu wielkości powoduje jakiś inny czynnik.
3. Aby wyprowadzić równanie. W takim przypadku możesz po prostu zastąpić w nim liczby i sprawdzić wartości nieznanej zmiennej.

Człowiek szuka przyczyn

Świadomość jest zorganizowana w taki sposób, że zdecydowanie musimy tłumaczyć wydarzenia, które się dzieją. Człowiek zawsze szuka związku między obrazem świata, w którym żyje, a informacją, którą otrzymuje. Często mózg tworzy porządek z chaosu. Łatwo może zauważyć związek przyczynowy tam, gdzie go nie ma. Naukowcy muszą nauczyć się przezwyciężyć ten trend. Zdolność do oceny związku między danymi jest obiektywnie konieczna w karierze akademickiej.

Tendencje w mediach

Zastanów się, jak można błędnie zinterpretować obecność łącza korelacji. Grupa brytyjskich uczniów o złym zachowaniu została zapytana, czy ich rodzice palili. Następnie test został opublikowany w gazecie. Wynik pokazał silną korelację między paleniem rodziców a przestępstwami ich dzieci. Profesor, który prowadził to badanie, zasugerował nawet ostrzeżenie paczek papierosów. Istnieje jednak wiele problemów z tym wnioskiem. Po pierwsze, korelacja nie pokazuje, która z tych wielkości jest niezależna. Dlatego można założyć, że uzależnienie rodziców spowodowane jest nieposłuszeństwem dzieci. Po drugie, niemożliwe jest stwierdzenie z całą pewnością, że oba problemy nie pojawiły się z powodu jakiegoś trzeciego czynnika. Na przykład rodziny o niskich dochodach. Należy odnotować emocjonalny aspekt wstępnych ustaleń profesora, który przeprowadził badanie. Był żarliwym przeciwnikiem palenia. Nic więc dziwnego, że w ten sposób zinterpretował wyniki swych badań.

Wnioski

Błędna interpretacja korelacji jako związku przyczynowego między dwiema zmiennymi może powodować haniebne błędy w badaniach. Problem polega na tym, że leży on w samym jądrze ludzkiej świadomości. Wiele sztuczek marketingowych opiera się na tej właśnie funkcji. Zrozumienie różnicy między przyczynowością a korelacją umożliwia racjonalną analizę informacji zarówno w życiu codziennym, jak i zawodowym.