Dziesiętne zaokrąglanie: uczenie się matematyki

Tak więc teraz zobaczymy, jak ma miejsce dziesiętne zaokrąglanie. W rzeczywistości proces ten nie jest tak skomplikowany, jak może się wydawać na pierwszy rzut oka. To prawda, że ​​niektóre dzieci w wieku szkolnym mają trudności z tym tematem. Pomóżmy im zrozumieć nasze dzisiejsze pytanie.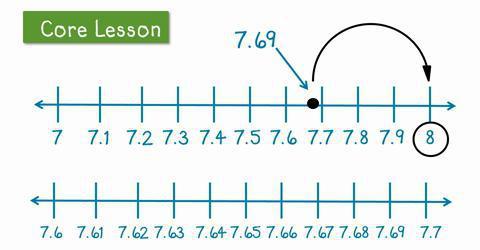

Pojęcie ułamka dziesiętnego

Przed zaokrągleniem miejsca dziesiętne, musimy jasno zrozumieć, z czym mamy do czynienia. Im lepiej zrozumiemy to pytanie, tym łatwiej będzie w przyszłości.

Ogólnie rzecz biorąc, pojęcie "ułamka dziesiętnego" ujawnia się w piątej klasie szkoły. Jest to rodzaj liczby składający się z części całkowitej i ułamkowej, której mianownik wynosi 10.

Aby jasno zrozumieć, o co toczy się gra, przyjrzyjmy się przykładowi, a następnie zbadaj, w jaki sposób zaokrąglane miejsca dziesiętne występują. Ten typ rekordu będzie wyglądał następująco: 5,26852. Jeśli tłumaczysz wynikową liczbę na ułamek, zobaczysz: 526852/100000. Dziesiętne ułamki mogą być zarówno dodatnie, jak i ujemne. To wszystko. A teraz chodźmy z nami do naszego problemu.

Częściowo

Chodzi o to, że zaokrąglanie ułamków dziesiętnych (stopień 6), z reguły, odbywa się w częściach. Najpierw zajmują resztę ("ogon"), czyli liczby, które są po przecinku. Tylko wtedy można przyjąć całą część.

Pierwszą rzeczą, która jest wymagana od nas, jest określenie dokładności, z jaką będziemy zaokrąglać ułamki dziesiętne. Do dziesiątych, setnych, tysięcznych i tak dalej. Następnie musisz przestrzegać pewnych zasad, a także nauczyć się jednego ważnego punktu, który zdecydowanie pomoże ci poradzić sobie z zadaniem. Pracujmy z wami na jasnym przykładzie. Podaj liczbę dowolną: 78 956 3245. Właśnie na nim przetestujemy regułę zaokrąglania miejsc dziesiętnych. Teraz go poznajemy.

Główna zasada

Podstawową zasadą, której musimy się nauczyć, jest wymiana liczb podczas zaokrąglania. Chodzi o to, że jest to dość łatwe do zrobienia. Zobaczmy dokładnie, jak.

Jeśli masz 0, 1, 2, 3 lub 4 jako cyfrę, zostanie ona automatycznie zamieniona na 0 i odrzucona. Następnie zbliż się do części całkowitej i spójrz na następny numer.

Gdy cyfra w cyfrze wynosi 5, 6, 7, 8 lub 9, będziesz musiał odrzucić tę część i dodać jedną do następnej (najbliższej części całkowitej). Ten proces należy powtórzyć do wybranej dokładności zaokrąglenia. Spójrzmy teraz na przykład z tobą. Na nim wszystko będzie wyglądało wyraźniej.

Przykład

Dlatego zaczynamy zaokrąglać u ciebie miejsca dziesiętne. Pracujemy z numerem 78,9563245. Zaokrąglamy je do dziesiątej, setnej i tysięcznej części. Spróbujmy.

Na początek odrzucamy całą część. Otrzymujemy 0.9563245. Będziemy kontynuować współpracę z Tobą z tym konkretnym numerem. Zaczynamy zaokrąglanie z tysięcznymi, stopniowo zwiększając dokładność.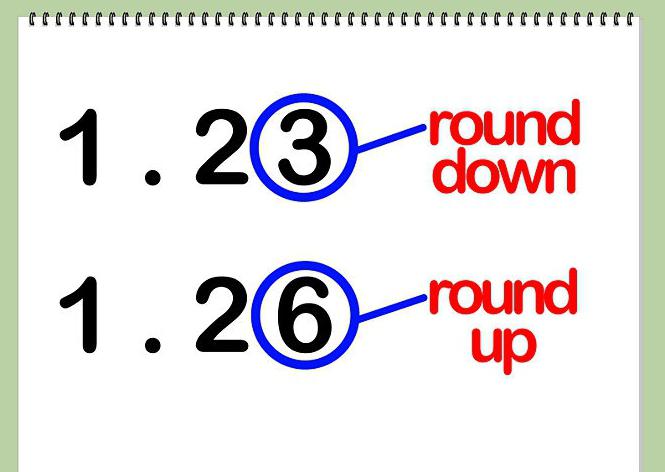

Liczba wynosi 0,9563245. Wracając do zera. Pierwsza liczba od końca to 5. Oznacza to, że "przekonwertujemy" ją na 0, i dodajemy 4 na 4. Druga cyfra - 4 + 1 = 5. Dlatego przypisujemy jednostkę do następnego znaku, a ta jest konwertowana na 0.

Do tej pory pracowaliśmy z Tobą: 0.95632 ⁽⁺¹⁾ . Zaokrąglanie do tysięcznej jest 3 cyframi. Kontynuujmy współpracę z Tobą. 2 + 1 = 3. Liczba ta jest mniejsza niż 5s. Więc zamień go na 0 i usuń. Następny etap to 3-ka. Nic nie jest do niego dodawane. Po prostu zamień na 0, ponieważ jest mniejszy niż 5. Zrobiliśmy to z tobą: 0.956. Teraz możesz dodać całą część: 78.956.

Ale nasze zaokrąglenie ułamków dziesiętnych się nie kończy. Teraz powinieneś trzymać ją setną. Aby to zrobić, tak jak poprzednio, patrzymy na ostatnią cyfrę po przecinku - 6. Zgodnie z regułą, zamieniamy ją na 0, a następnie dodajemy 1 do cyfry po lewej stronie, otrzymujemy 78,96. Zaokrąglanie do dziesiątek tutaj nie jest zbyt odpowiednie. Otrzymujemy z tobą liczbę całkowitą. W końcu 6-ka zostanie zastąpione przez 0, jednostka zostanie dodana do 9, a na końcu otrzymamy: 78,9 ⁽⁺¹⁾ . To się skończy 79. To wszystko. Teraz wiesz, jak zaokrąglać ułamki.