Discriminant: przykłady rozwiązań. Jak rozwiązywać równania kwadratowe przez dyskryminację
Równania kwadratowe często pojawiają się podczas rozwiązywania różnych problemów fizyki i matematyki. W tym artykule przyjrzymy się, jak rozwiązać te równości w sposób uniwersalny "poprzez dyskryminację". Przykłady wykorzystania zdobytej wiedzy podane są również w artykule.
Jakie równania mówimy?
Poniższy rysunek przedstawia wzór, w którym x jest nieznaną zmienną, a łacińskie znaki a, b, c to niektóre znane liczby.
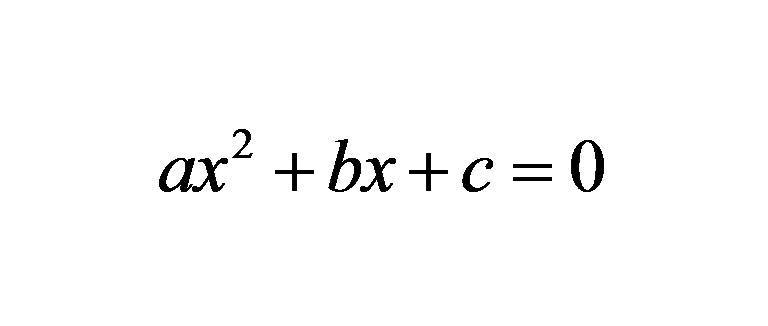
Każdy z tych symboli nazywany jest współczynnikiem. Jak widać, liczba "a" znajduje się przed zmienną x do kwadratu. Jest to reprezentowany maksymalny stopień ekspresji, więc nazywa się to równaniem kwadratowym. Często używana jest jego inna nazwa: równanie drugiego rzędu. Wartość sama w sobie jest kwadratowym współczynnikiem (stojącym ze zmienną do kwadratu), b jest współczynnikiem liniowym (znajduje się obok zmiennej podniesionej do pierwszej mocy), a na końcu liczba c jest pojęciem wolnym.
Zauważ, że typ równania, pokazany na powyższym rysunku, jest wspólnym klasycznym kwadratowym wyrażeniem. Oprócz tego istnieją inne równania drugiego rzędu, w których współczynniki b, c mogą wynosić zero.
Gdy zadaniem jest rozwiązanie rozważanej równości, oznacza to, że należy znaleźć takie wartości zmiennej x, które by ją usatysfakcjonowały. Tutaj pierwszą rzeczą do zrobienia jest zapamiętanie następującej rzeczy: ponieważ maksymalny stopień X wynosi 2, ten typ ekspresji nie może zawierać więcej niż 2 rozwiązania. Oznacza to, że jeśli podczas rozwiązywania równania znaleziono 2 wartości x, które go spełniają, to możesz być pewien, że nie ma trzeciej cyfry, zastępując ją zamiast x równością również. Rozwiązania równań w matematyce nazywają to korzeniami.
Sposoby rozwiązywania równań drugiego rzędu
Rozwiązywanie równań tego typu wymaga znajomości niektórych teorii na ich temat. W szkolnym kursie algebry rozważa się 4 różne metody rozwiązania. Wymieniamy je:
- przy użyciu faktoryzacji;
- używając wzoru na cały kwadrat;
- zastosowanie wykresu odpowiedniej funkcji kwadratowej;
- stosując równanie dyskryminacyjne.
Plus pierwszą metodą jest jej prostota, jednak nie można jej zastosować do wszystkich równań. Druga metoda jest uniwersalna, ale nieco uciążliwa. Trzecia metoda wyróżnia się jasnością, ale nie zawsze jest wygodna i odpowiednia. I wreszcie, użycie równania dyskryminacyjnego jest uniwersalnym i dość prostym sposobem znalezienia korzeni absolutnie dowolnego równania drugiego rzędu. Dlatego w artykule rozważamy tylko to.
Wzór na uzyskanie korzeni równania
Przejdźmy do ogólnej postaci równania kwadratowego. Zapisujemy to: a * x² + b * x + c = 0. Przed użyciem metody rozwiązania "przez dyskryminatora" konieczne jest zmniejszenie równości zawsze do zapisanej formy. Oznacza to, że musi składać się z trzech terminów (lub mniej, jeśli b lub c wynosi 0).
Na przykład, jeśli istnieje wyrażenie: x2-9 * x + 8 = -5 * x + 7 * x ², to powinieneś najpierw przenieść wszystkie jego elementy na tę samą stronę równania i dodać warunki zawierające zmienną x w równych mocach.
W takim przypadku operacja ta spowoduje następujące wyrażenie: -6 * x²-4 * x + 8 = 0, co jest równoważne z równaniem 6 * x² + 4 * x-8 = 0 (tutaj pomnożyliśmy lewą i prawą stronę równości przez -1) .
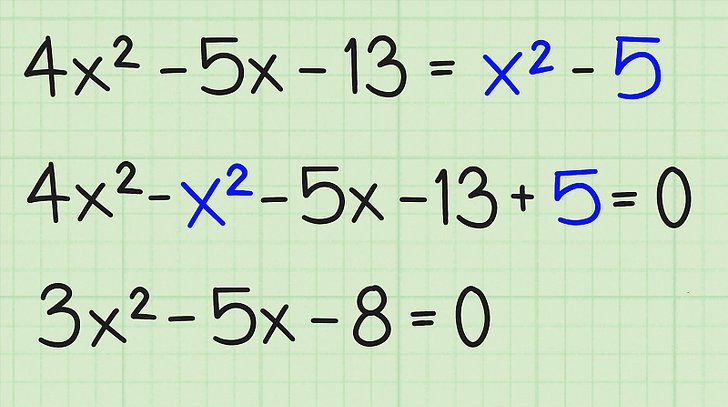
Po nauczeniu powyższego kroku powinieneś nauczyć się rozróżniać współczynniki. Tutaj wszystko jest proste: kiedy x2 jest zawsze a, gdy x 1 to b, to wolny czas c jest liczbą, która nie jest powiązana z x.
W powyższym przykładzie a = 6, b = 4, c = -8. Zauważ, że wszyscy członkowie rozpatrywanej równości są zawsze sumowani między sobą, dlatego jeśli pojawi się znak "-", oznacza to, że odpowiedni współczynnik jest ujemny, jak c w tym przypadku.
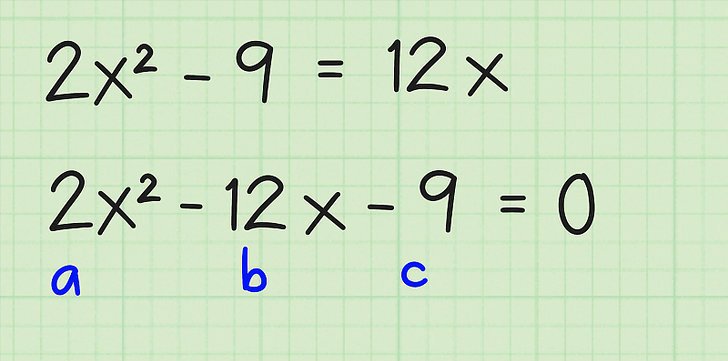
Po przeanalizowaniu tego momentu zwracamy się teraz do samej formuły, która pozwala uzyskać korzenie równania kwadratowego. Wygląda na to, jak pokazano na poniższym zdjęciu.
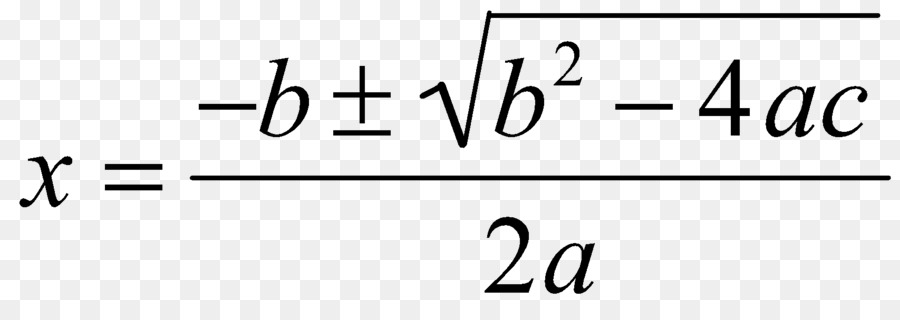
Jak widać z tego wyrażenia, pozwala uzyskać dwa korzenie (należy zwrócić uwagę na znak "±"). Aby to zrobić, wystarczy podstawić współczynniki b, c i a.
Pojęcie dyskryminatora
W poprzednim akapicie podano formułę, która pozwala szybko rozwiązać równanie drugiego rzędu. W nim wyrażenie root jest nazywane dyskryminatorem, czyli D = b²-4 * a * c.
Dlaczego ta część formuły jest odizolowana, a nawet ma swoją własną nazwę? Faktem jest, że dyskryminator łączy wszystkie trzy współczynniki równania w jedno wyrażenie. Ten ostatni fakt oznacza, że w pełni przenosi informacje o korzeniach, które można wyrazić na poniższej liście:
- D> 0: równość ma 2 różne rozwiązania, obie są liczbami rzeczywistymi.
- D <0: dwa korzenie są również uzyskane, ale oba są złożone. Ten rodzaj ekspresji nauczył się rozwiązywać jedynie w okresie renesansu, kiedy to wprowadzono pojęcie "jednostki urojonej" przez matematyków nowego czasu.
- D = 0: równanie ma tylko jeden rdzeń i jest to liczba rzeczywista.
Artykuł zawiera ponadto przykłady dyskryminacyjnych równań kwadratowych i ich rozwiązania.
Zadanie wyznaczania dyskryminatora
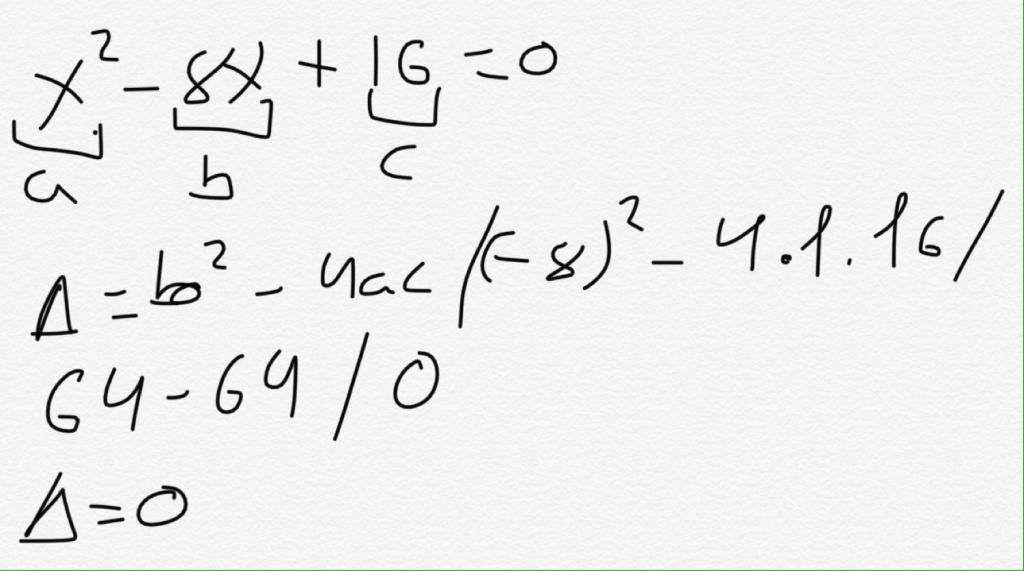
Podajemy prosty przykład znalezienia dyskryminatora. Należy podać następującą równość: 2 * x² - 4 + 5 * x-9 * x² = 3 * x-5 * x² + 7.
Wprowadzamy go do standardowego formularza, otrzymujemy: (2 * x²-9 * x² + 5 * x²) + (5 * x-3 * x) + (- 4-7) = 0, skąd dochodzimy do równości: -2 * x ² + 2 * x-11 = 0. Tutaj a = -2, b = 2, c = -11.
Teraz możesz użyć wzoru dla dyskryminatora: D = 2² - 4 * (- 2) * (- 11) = -84. Wynikowa liczba jest odpowiedzią na zadanie. Ponieważ w tym przykładzie dyskryminator jest mniejszy od zera, można powiedzieć, że to równanie kwadratowe nie ma prawdziwych korzeni. Jego decyzja będzie tylko liczbą złożonego typu.
Przykład nierówności przez dyskryminującego
Rozwiązujemy problemy nieco innego typu: podana równość to -3 * x²-6 * x + c = 0. Konieczne jest znalezienie wartości c, dla których D> 0.
W tym przypadku znane są tylko 2 z 3 współczynników, dlatego dokładna wartość dyskryminatora nie może być obliczona, ale wiadomo, że jest dodatnia. Ten ostatni fakt służy do konstruowania nierówności: D = (-6) ²-4 * (- 3) * c> 0 => 36 + 12 * c> 0. Rozwiązanie wynikłej nierówności prowadzi do wyniku: c> -3.
Sprawdź wynikowy numer. Aby to zrobić, obliczamy D dla 2 przypadków: c = -2 i c = -4. Liczba -2 spełnia uzyskany wynik (-2> -3), odpowiedni wyróżnik będzie miał wartość: D = 12> 0. Z kolei liczba -4 nie spełnia nierówności (-4 <-3), obliczamy dyskryminację: D = -12 <0, co jest sprzeczne z warunkiem problemu.
Tak więc każda liczba c większa niż -3 spełni warunek.
Przykład rozwiązania równania
Prezentujemy problem, który polega nie tylko na znalezieniu dyskryminatora, ale także na rozwiązaniu równania. Konieczne jest znalezienie korzeni dla równości -2 * x² + 7-9 * x = 0.
W tym przykładzie dyskryminator jest równy następującej wartości: D = 81-4 * (- 2) * 7 = 137. Następnie korzenie równania są zdefiniowane jako: x = (9 ± √137) / (- 4). Są to dokładne wartości korzeni, jeśli obliczymy przybliżony rdzeń, otrzymamy liczby: x = -5.176 i x = 0.676.
Problem geometryczny
Rozwiążemy problem, który będzie wymagał nie tylko umiejętności obliczania dyskryminatora, ale także zastosowania umiejętności abstrakcyjnego myślenia i wiedzy, jak tworzyć równania kwadratowe.
Bob miał kołdrę o wymiarach 5 x 4 metry. Chłopiec chciał uszyć go na obwodzie solidnego paska z pięknej tkaniny. Jak gruby będzie ten pasek, jeśli wiadomo, że Bob ma 10 m² tkaniny.

Niech pasek ma grubość x m, wówczas powierzchnia tkaniny wzdłuż dłuższego boku koca będzie (5 + 2 * x) * x, a ponieważ długie boki to 2, mamy: 2 * x * (5 + 2 * x). Po krótkiej stronie powierzchnia szytego materiału będzie 4 * x, ponieważ te strony wynoszą 2, otrzymujemy wartość 8 * x. Zwróć uwagę, że wartość 2 * x została dodana do dłuższego boku, ponieważ długość koca wzrosła o tę liczbę. Całkowita powierzchnia tkaniny przyszytej do koca wynosi 10 m². Dlatego uzyskujemy równość: 2 * x * (5 + 2 * x) + 8 * x = 10 => 4 * x² + 18 * x-10 = 0.
W tym przykładzie dyskryminatorem jest: D = 18²-4 * 4 * (- 10) = 484. Jego korzeń wynosi 22. Wykorzystując wzór, znajdujemy pożądane korzenie: x = (-18 ± 22) / (2 * 4) = (- 5; 0,5). Oczywiście, z dwóch korzeni, tylko liczba 0.5 jest odpowiednia dla stanu problemu.
W ten sposób pasek materiału, który Bob przyszyje do koca, ma szerokość 50 cm.