Przykłady obliczania powierzchni cylindra
Istnieje wiele zadań związanych z cylindrem. Muszą znaleźć promień i wysokość ciała lub rodzaj jego przekroju. Dodatkowo czasami musisz obliczyć powierzchnię cylindra i jego objętość.
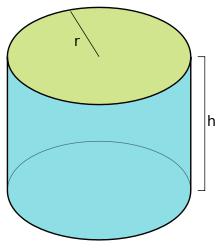
Które ciało jest cylindrem?
W trakcie nauki szkolnej program jest badany na okrągło, czyli będąc w bazie, w cylindrze. Ale jest też eliptyczny widok tej figury. Z tytułu jest oczywiste, że jego podstawą będzie elipsa lub owal.
Istnieją dwie bazy cylindrów. Są one równe sobie nawzajem i połączone są segmentami, które łączą odpowiednie punkty baz. Nazywane są generatorami cylindrycznymi. Wszystkie generatory są równoległe do siebie i równe. Stanowią boczną powierzchnię ciała.
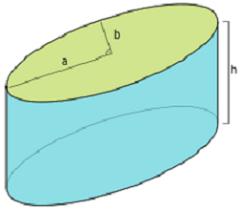
Ogólnie rzecz biorąc, cylinder jest ciałem pochyłym. Jeśli generatory tworzą kąt prosty z podstawami, to już mówią o prostej figurze.
Co ciekawe, okrągły cylinder jest obracającym się korpusem. Uzyskuje się ją, obracając prostokąt wokół jednego z jego boków.
Główne elementy cylindra
Główne elementy cylindra są następujące.
- Wysokość Jest to najkrótsza odległość między podstawami cylindra. Jeśli jest prosty, to wysokość pokrywa się z generatrix.
- Promień Zbiega się z tym, który można trzymać w bazie.
- Oś. Jest to linia prosta, która zawiera środki obu zasad. Oś jest zawsze równoległa do wszystkich generatorów. W prostym cylindrze jest prostopadły do podstaw.
- Przekrój osiowy. Powstaje na przecięciu cylindra przez płaszczyznę zawierającą oś.
- Styczna płaszczyzna. Przechodzi przez jeden z generatorów i jest prostopadły do odcinka osiowego, który jest przeciągany przez ten generator.
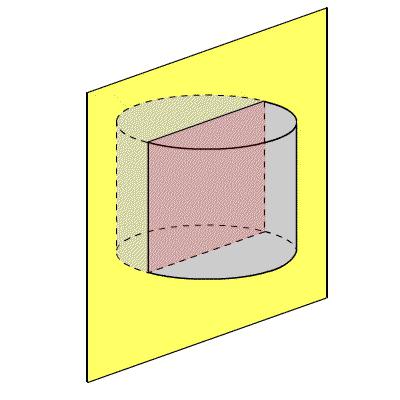
W jaki sposób cylinder połączony z pryzmatem jest w nim wpisany lub opisany w pobliżu?
Czasami zdarzają się zadania, w których konieczne jest obliczenie powierzchni cylindra, podczas gdy znane są niektóre elementy powiązanego pryzmatu. Jak odnoszą się te liczby?
Jeśli pryzmat jest wpisany w cylinder, wówczas jego podstawy są równymi wielokątami. Są one wpisane w odpowiednią podstawę cylindra. Boczne krawędzie pryzmy pokrywają się z generatorami.
Na opisanym pryzmie w bazach znajdują się regularne wielokąty. Są one opisane wokół kręgów cylindrowych, które są jego podstawami. Płaszczyzny zawierające powierzchnie pryzmatu dotykają cylindra wzdłuż generatorów.
Na powierzchni bocznej powierzchni i podstawy dla prostego okrągłego cylindra
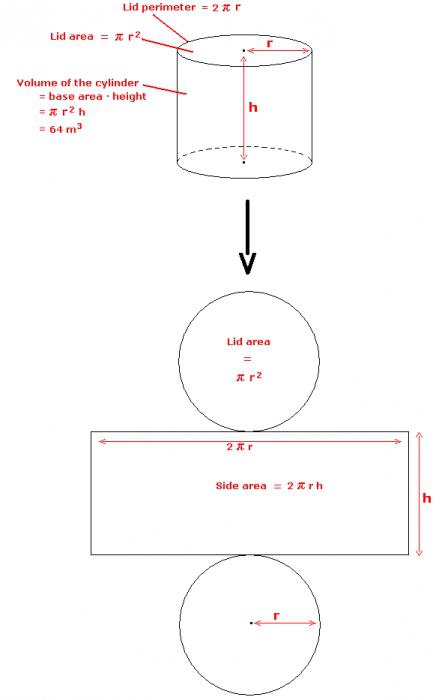
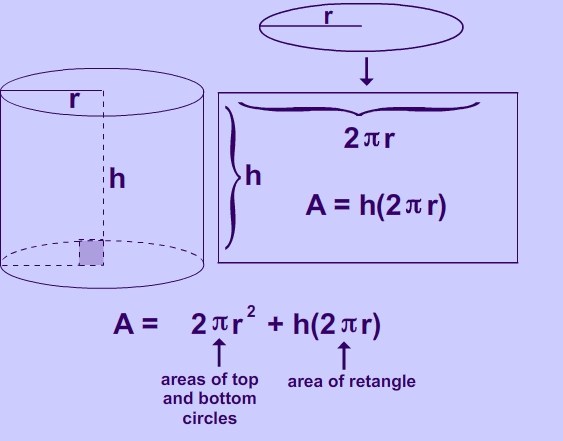
Jeśli skanujesz powierzchnię boczną, otrzymujesz prostokąt. Jego boki będą się pokrywać z generatorem i obwód tereny. Dlatego powierzchnia boczna cylindra będzie równa iloczynowi tych dwóch wielkości. Jeśli napiszesz formułę, otrzymasz następujące informacje:
S bok = l * n,
gdzie n jest generatorem, l jest długością okręgu.
Ostatni parametr jest obliczany według wzoru:
l = 2 π * r,
tutaj r jest promieniem okręgu, π jest liczbą "pi" równą 3,14.
Ponieważ podstawą jest koło, jego powierzchnia jest obliczana za pomocą następującego wyrażenia:
S primary = π * r 2 .
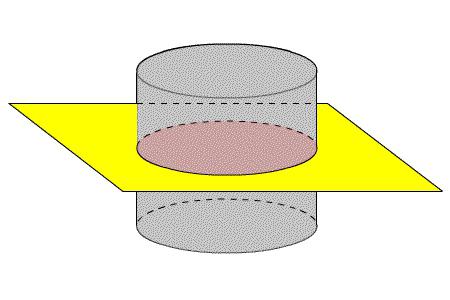
Na powierzchni całej powierzchni prostego okrągłego cylindra
Ponieważ składa się ona z dwóch zasad i powierzchni bocznej, te trzy wielkości należy dodać. Oznacza to, że całkowita powierzchnia cylindra zostanie obliczona według wzoru:
S floor = 2 π * r * n + 2 π * r 2 .
Często jest napisane w innej formie:
S floor = 2 π * r (n + r).
Na obszarach pochyłego okrągłego cylindra
Jeśli chodzi o podstawy, wszystkie formuły są tam takie same, ponieważ nadal są okręgami. Ale powierzchnia boczna nie daje prostokąta.
Aby obliczyć powierzchnię boczną nachylonego cylindra, konieczne będzie pomnożenie wartości generatora i obwodu przekroju, który będzie prostopadły do wybranego generatora.
Formuła wygląda następująco:
S bok = x * P,
gdzie x - długość cylindra generatora, P - obwód przekroju.
Sekcja, nawiasem mówiąc, lepiej wybrać tak, że tworzy elipsę. Następnie obliczenia jego obwodu zostaną uproszczone. Długość elipsy jest obliczana za pomocą formuły, która daje przybliżoną odpowiedź. Ale często wystarczy do zadań szkolnych:
l = π * (a + c),
gdzie "a" i "b" są półosiami elipsy, to jest odległością od środka do jej najbliższych i najdalszych punktów.
Obszar całej powierzchni należy obliczyć za pomocą następującego wyrażenia:
S piętro = 2 π * r 2 + x * R.
Jakie są sekcje prostego okrągłego cylindra?
Gdy odcinek przechodzi przez oś, jego obszar jest definiowany jako iloczyn generatora i średnicy podstawy. Wynika to z faktu, że ma on kształt prostokąta, którego boki pokrywają się ze wskazanymi elementami.
Aby znaleźć przekrój poprzeczny cylindra, który jest równoległy do osiowego, potrzebujemy również wzoru na prostokąt. W tej sytuacji jedna strona nadal będzie pokrywała się z wysokością, a druga równa będzie cięciwie podstawy. Ta ostatnia pokrywa się z linią przekroju wzdłuż podstawy.
Kiedy przekrój jest prostopadły do osi, ma kształt koła. Co więcej, jego powierzchnia jest taka sama jak u podstawy figury.
Być może nawet skrzyżowanie pod pewnym kątem do osi. Następnie w przekroju uzyskano owal lub jego część.
Przykłady zadań
Numer zadania 1. Podano prosty cylinder, którego podstawowa powierzchnia wynosi 12,56 cm 2 . Konieczne jest obliczenie całkowitej powierzchni cylindra, jeżeli jego wysokość wynosi 3 cm.
Decyzja. Konieczne jest użycie wzoru na pełny obszar okrągłego cylindra prostego. Brakuje jednak danych, a mianowicie promienia bazy. Ale obszar koła jest znany. Z tego łatwo obliczyć promień.
Jest równy pierwiastkowi kwadratowemu ilorazu, który uzyskuje się przez podzielenie obszaru bazy przez pi. Po podzieleniu 12,56 przez 3,14 wychodzi 4. Pierwiastek kwadratowy z 4 wynosi 2. Dlatego promień będzie miał dokładnie tę wartość.
Teraz możesz obliczyć obszar powierzchni bocznej. Aby to zrobić, pomnóż pi przez promień, wysokość i 2. Praca będzie wyglądać następująco: 3.14 * 3 * 2 * 2. Wynik działania: 37,68 cm 2 .
Aby policzyć całkowitą powierzchnię, należy dodać dwie podstawy (12,56 cm 2 ) i powierzchnię boczną (37,68 cm 2 ). Wynikiem jest liczba 50,24 cm 2 .
Odpowiedź: S płci = 50,24 cm 2 .
Zadanie numer 2. Cylinder o promieniu 5 cm jest tłumiony przez płaszczyznę równoległą do osi. Odległość od przekroju do osi wynosi 3 cm, wysokość cylindra wynosi 4 cm, wymagane jest znalezienie obszaru przekroju.
Decyzja. Kształt przekroju jest prostokątny. Jedna strona odpowiada wysokości cylindra, a druga jest równa cięciwie. Jeśli pierwsza wartość jest znana, należy znaleźć drugą.
Aby to zrobić, wykonaj dodatkową konstrukcję. U podstawy wykonujemy dwa segmenty. Obie rozpoczną się w środku okręgu. Pierwszy zakończy się w środku akordu i będzie równy znanej odległości od osi. Drugi jest na końcu akordu.
Zdobądź trójkąt prostokątny. Znana jest przeciwprostokątna i jedna z nóg. Hipotenada pokrywa się z promieniem. Druga noga to połowa akordu. Nieznana noga, pomnożona przez 2, da pożądaną długość akordu. Obliczamy jego wartość.
Aby znaleźć nieznaną nogę, musisz wyrównać przeciwprostokątną i znaną nogę, odjąć sekundę od pierwszej i wziąć pierwiastek kwadratowy. Kwadraty mają 25 i 9. Różnica wynosi 16. Po ekstrakcji pierwiastek kwadratowy 4. To jest pożądana noga.
Akord będzie równy 4 * 2 = 8 (cm). Teraz możesz obliczyć powierzchnię przekroju: 8 * 4 = 32 (cm 2 ).
Odpowiedź: S Sich ma 32 cm 2 .
Zadanie numer 3. Konieczne jest obliczenie osiowej sekcji cylindra. Wiadomo, że jest w nim wpisany sześcian o boku 10 cm.
Decyzja. Osiowy odcinek cylindra pokrywa się z prostokątem, który przechodzi przez cztery wierzchołki sześcianu i zawiera przekątne jego podstaw. Strona sześcianu jest generatorem cylindra, a przekątna podstawy pokrywa się ze średnicą. Iloczyn tych dwóch wielkości daje obszar do rozpoznania w problemie.
Aby znaleźć średnicę, musisz użyć wiedzy, że u podstawy kostki jest kwadrat, a jej przekątna tworzy trójkąt równoboczny. Jego przeciwprostokątna jest pożądanym ukośnym kształtem.
Aby to obliczyć, potrzebna jest formuła twierdzenia Pitagorasa. Konieczne jest wyrównywanie boków sześcianu, pomnożenie przez 2 i wyodrębnienie pierwiastka kwadratowego. Dziesięć do drugiego stopnia to sto. Pomnożone przez 2 - dwieście. Kwadrat o wartości 200 wynosi 10√2.
Sekcja to ponownie prostokąt z bokami 10 i 10√2. Jego obszar jest łatwy do zliczenia przez pomnożenie tych wartości.
Odpowiedź jest. S sech = 100 √ 2 cm 2 .