Znajdź pierwiastek równania? To jest łatwe!
W matematyce istnieje wiele równań. Zawsze trzeba je rozwiązywać, to znaczy szukać wszystkich liczb, które sprawią, że będzie to prawdziwa równość. Sposoby znajdowania rozwiązań są określane przez oryginalną formę równania. Będzie to również zależało od liczby prawdziwych wartości zmiennej, które są wyznaczone jako pierwiastek równania. Ta liczba może być różna od zera do nieskończoności.
Co oznacza równanie i jego źródło?
Z tytułu oczywiste jest, że przyrównuje dwie wartości, które można przedstawić za pomocą wyrażeń numerycznych lub alfabetycznych. Ponadto zawierają wciąż nieznane ilości. Najprostsze równanie ma tylko jeden.
Istnieje wiele rodzajów równań, ale koncepcja korzenia jest dla nich zawsze taka sama. Korzeniem równania jest taka wartość nieznanej liczby, przy której równanie zakłada prawdziwą równość. Zdarzają się sytuacje, gdy istnieje kilka takich liczb, wtedy nieznane nazywa się zmienną.
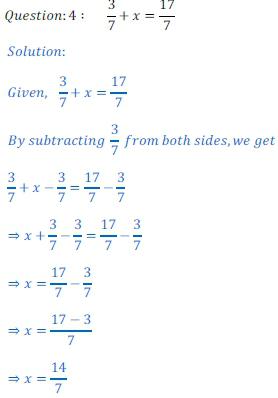
Znalezienie wszystkich możliwych źródeł równania jest jego rozwiązaniem. Oznacza to, że musisz wykonać serię operacji matematycznych, które ją upraszczają. A potem doprowadzić do równości, która zawiera tylko nieznane i liczbę.
W algebrze, przy rozwiązywaniu równań, można dojść do sytuacji, że nie będzie żadnych korzeni. Następnie mówią, że jest nierozpuszczalny. A w odpowiedzi na takie równanie trzeba zapisać, że nie ma rozwiązań.
Ale czasami dzieje się odwrotnie. Oznacza to, że obce korzenie pojawiają się w procesie licznych przemian. Nie zastąpią prawdziwej równości. Dlatego liczby powinny być zawsze sprawdzane, aby uniknąć sytuacji z niepotrzebnymi korzeniami w odpowiedzi. W przeciwnym razie równanie nie zostanie uznane za rozwiązane.
O równaniu liniowym
Zawsze można go przekształcić w zapis następującej postaci: a * x + v = 0. W nim "a" jest zawsze niezerowe. Aby zrozumieć, ile korzeni ma równanie, trzeba będzie je rozwiązać w ogólnej formie.
Transformacje algorytmów:
- przesuń termin "w" na prawą stronę równości, zastępując jego znak przeciwną;
- dzielą obie strony wynikłej równości przez współczynnik "a".
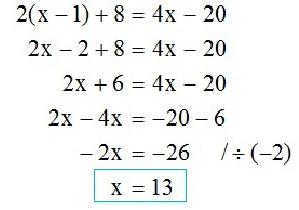
Ogólny pogląd na rozwiązanie to:
x = -in / a .
Wynika z niego jasno, że odpowiedź to jeden numer. To tylko jeden root.
Równanie kwadratowe
Jego ogólna postać: a * x 2 + b * x + c = 0 . Tutaj współczynniki są dowolnymi liczbami z wyjątkiem pierwszego, "a", które nie może być równe zeru. W końcu stanie się on automatycznie liniowy. Odpowiedź na pytanie, ile korzeni ma równanie, nie jest już tak prosta jak w poprzednim przypadku.
Wszystko będzie zależeć od wartości dyskryminatora. Oblicza się ją za pomocą wzoru D = w 2 - 4 a * s . Po obliczeniach "D" może okazać się większe, mniejsze lub równe zeru. W pierwszym przypadku korzenie równania będą dwa, w drugim odpowiedź będzie "bez korzeni", a trzecia sytuacja da tylko jedną nieznaną wartość.
Formuły używane do znalezienia pierwiastków równania kwadratowego i zawierające wyróżnik
W ogólnym przypadku, gdy "D" jest liczbą dodatnią, nie równą zeru, należy użyć następującej formuły:
х 1,2 = (-в ± √Д) / (2 * а) .
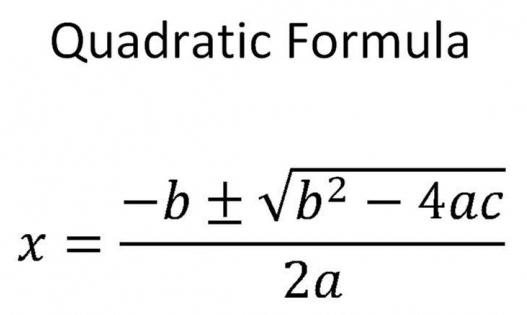
Zawsze są tu dwie odpowiedzi. Wynika to z faktu, że oryginalna formuła jest znakiem plus / minus. Znacząco zmienia wartość nieznanego.
Gdy "D" jest równe zero, korzeń równania jest jedyną liczbą. Tylko dlatego pierwiastek kwadratowy od zera wynosi zero. Zatem dodawanie i odejmowanie musi wynosić zero. Od tego numeru się nie zmieni. Dlatego też wzór pierwiastka równania można zapisać bez wymieniania "D":
x = (-v) / (2 * a).
Jeśli dyskryminator jest ujemny, nie można wyodrębnić z niego pierwiastka kwadratowego. Dlatego korzenie takiego równania nie będą.
Uwaga Dotyczy to kursu szkolnego, który nie jest nauczany. liczby zespolone. Po ich wprowadzeniu okazuje się, że w tej sytuacji będą dwie odpowiedzi.
Wzory do obliczania pierwiastków równania kwadratowego, które nie używają dyskryminacji
Mówimy o twierdzeniu Viet. Jest on ważny w przypadku, gdy równanie kwadratowe jest napisane w nieco innej formie:
x 2 + c * x + c = 0.
Następnie formuła root równanie kwadratowe sprowadza się do rozwiązania dwóch liniowych:
x 1 + x 2 = -in
i
x 1 * x 2 = s.
Jest to rozwiązane ze względu na fakt, że wyrażenie dla jednego z korzeni pochodzi z pierwszego. I ta wartość musi być podstawiona do drugiej. Tak więc drugi root zostanie znaleziony, a następnie pierwszy.
Ta opcja zawsze może pochodzić z ogólnej postaci równania kwadratowego.
Wystarczy podzielić wszystkie współczynniki na "a".
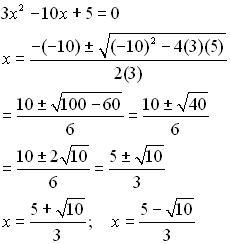
Co jeśli potrzebujesz znać najmniejszą wartość roota?
Rozwiąż równanie i znajdź wszystkie możliwe liczby, które są odpowiednie dla odpowiedzi. A następnie wybierz najmniejszy. To będzie najmniejszy pierwiastek równania.
Najczęściej takie pytania znajdują się w zadaniach, które mają stopień większy niż 2 lub zawierają funkcje trygonometryczne. Przykładem, kiedy trzeba znaleźć najmniejszy root, jest następująca równość:
2 x 5 + 2 x 4 - 3 x 3 - 3 x 2 + x + 1 = 0.
Aby znaleźć każdą wartość, którą można nazwać "korzeniem równania", równanie to musi zostać przekształcone. Pierwsze działanie: grupowanie członków w pary: pierwsze z drugim i tak dalej. Następnie z każdej pary, aby utworzyć wspólny czynnik.
W każdym nawiasie pozostanie (x + 1). Wspólnym czynnikiem w pierwszej parze będzie 2 x 4 , w drugim 3 x 2 . Teraz znowu trzeba wprowadzić wspólny czynnik, który będzie taki sam.
Po mnożniku (x + 1) będzie (2 x 4 - 3 x 2 + 1). Iloczyn dwóch czynników wynosi zero, tylko jeśli jeden z nich przyjmuje wartość równą zeru.
Pierwszy nawias wynosi zero dla x = -1. To będzie jeden z korzeni równania.
Inne zostaną uzyskane z równania utworzonego przez drugi nawias, zrównane do zera. Jest dwukierunkowy. Aby go rozwiązać, musisz wpisać notację: x 2 = y. Następnie równanie zmieni się znacząco i przybędzie zwykłą formą równania kwadratowego.
Jego dyskryminatorem jest D = 1. Jest większy od zera, co oznacza, że będą dwa korzenie. Pierwszy root jest równy 1, drugi wynosi 0,5. Ale są to wartości dla y.
Konieczne jest przywrócenie wprowadzonego oznaczenia. x 1,2 = ± 1, x 3,4 = ± 0,0. Wszystkie pierwiastki równania: -1; 1; -√0,5; √0,5. Najmniejszy z nich to -1. To jest odpowiedź.
Na zakończenie
Przypomnienie: wszystkie równania wymagają sprawdzenia, czy root jest odpowiedni. Może on jest nieznajomym? Warto sprawdzić proponowany przykład.
Jeśli podstawimy jednostkę w początkowo podanym równaniu zamiast "x", wówczas okaże się, że 0 = 0. Ten korzeń jest poprawny.
Jeśli x = -1, wynik jest taki sam. Korzeń jest również odpowiedni.
Podobnie, gdy wartości "x" są równe √0,5 i √0,5, prawdziwa równość znowu pojawia się. Wszystkie korzenie pasują.
Ten przykład nie daje dodatkowych korzeni. Nie zawsze tak jest. Możliwe, że najmniejsza wartość nie byłaby odpowiednia do testowania. Potem musiałbym wybrać resztę.
Wniosek: należy pamiętać o kontroli i ostrożnie podejść do rozwiązania.