Dyfrakcja Fresnela na okrągłym otworze i dysku

Dyfrakcja światła objawia się falą świetlną pochylającą się wokół małych przeszkód, podczas gdy obserwowane są odchylenia od praw optyki geometrycznej. Dotyczy to również fal świetlnych przechodzących przez otwór, na przykład w obiektywie kamery lub źrenicy oka. Występuje dyfrakcja Fresnela i Fraunhofera. Różnice polegają na wielkości odległości między źródłem światła, przeszkodą i ekranem, na którym obserwuje się obraz tego zjawiska.

Miejsce dyfrakcji w ogólnej serii zjawisk optycznych

Przejście światła (i ogólnie fale elektromagnetyczne przez różne niejednorodne ośrodki towarzyszą zjawiska ich odbicia, dyfrakcji i refrakcji. Kiedy fala osiąga granicę dwóch mediów, dzieli się ją na odbity, który pozostaje na pierwotnym nośniku, ale ze zmianą kierunku propagacji i załamuje się, która przechodzi przez granicę nośnika, ale także ze zmianą kierunku. Dyfrakcja Fresnela jest procesem zmiany kierunku fali świetlnej, gdy napotyka nie granice dwóch mediów, ale pewną nieprzejrzystą przeszkodę z otworem (lub bez niego, ale małe wymiary) w tym samym medium. Stopień dyfrakcji wzrasta wraz ze wzrostem długości fali świetlnej.

Zjawisko odkrywania

Prawdopodobnie pierwszym, który zaobserwował dyfrakcję, był Francesco Maria Grimaldi (2 kwietnia 1618 - 28 grudnia 1663), włoski jezuicki kapłan, a jednocześnie matematyk i fizyk, który uczył w kolegium jezuickim w Bolonii. Drugą połowę życia poświęcił studiowaniu astronomii i optyki.

Grimaldi słynął z pracy zatytułowanej "Fizyczna nauka światła, kwiatów i tęczy", która została opublikowana w Bolonii w 1665 roku. Większość składa się z żmudnej dyskusji o naturze światła z teologicznego punktu widzenia i nie jest dziś przedmiotem zainteresowania. Jednak książka zawiera także opis licznych eksperymentów związanych z dyfrakcją promieni świetlnych.

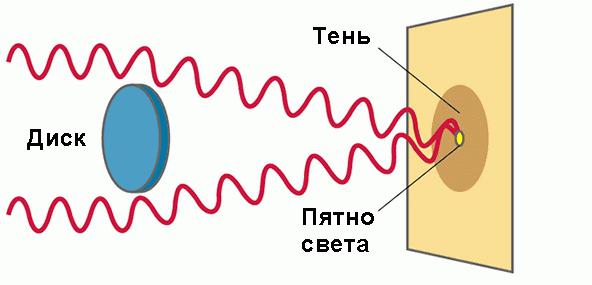
Bazując na codziennym doświadczeniu, ludzie w czasach starożytnych doszli do wniosku, że promienie światła rozchodzą się po liniach prostych. Wszak obiekt, który znajduje się między, na przykład, płomieniem świecy a ścianą, rzuca cień ostrym obramowaniem, tak jakby bezpośrednie promienie światła odrywały się na nieprzezroczystej barierze.

Jednak wyniki eksperymentów Grimaldi były sprzeczne z tymi pomysłami, które zostały ustanowione przez tysiące lat. Okazuje się, że jeśli oświetlisz różne obiekty przez przeszkodę z małym otworem, to cienie z nich nie będą takie same jak przy braku przeszkody. Okazało się, że światło może zmieniać kierunek propagacji i pokonywać drobne przeszkody.

Jak wykryto dyfrakcję Fresnela na okrągłym otworze

Grimaldi, przekazując światło słońca do ciemnego pomieszczenia przez mały otwór (otwór), zauważył, że szerokość cienia cienkich przedmiotów, takich jak igły i włosy na ekranie, jest znacznie większa (jak widać na poniższym zdjęciu), niż gdyby promienie światła przeszły proste linie.

Zauważył również, że krąg światła uformowany na ekranie przez promienie przechodzące przez bardzo mały otwór w płycie prowadzącej był wyraźnie większy, niż gdyby promienie te padały prosto na ekran. Grimaldi stwierdził, że zmieniają kierunek podczas przechodzenia w pobliżu krawędzi dziury.

W swoich eksperymentach przeprowadzonych w tym samym pomieszczeniu, do którego wpadało światło przez otwory w okiennicach, odległość między przeszkodą dla fal świetlnych (płyta z okrągłym otworem) a ekranem była niewielka. Dyfrakcja Fresnela również odpowiada tym warunkom. Analizując to, nie możemy zaniedbać krzywizny frontu jako pierwszej fali padającej na przeszkodę i fal drugorzędnych. Dają ekranowi obraz dyfrakcyjny przeszkody z dziurą, jak pokazano na poniższym zdjęciu.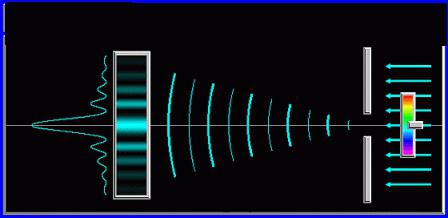

Co się stanie, jeśli światło pada na małą nieprzejrzystą przeszkodę

Grimaldi odkrył również, że cień małego ciała (o nieregularnym kształcie) został otoczony przez trzy kolorowe paski lub wstążki, które zwęziły się, gdy oddalały się od centrum cienia. Jeśli pierwotny strumień światła był mocniejszy, odtwarzał podobne pasma koloru w obszarze samego cienia: występowały dwa lub więcej takich pasm, a ich liczba wzrastała proporcjonalnie do odległości między cieniem a oświetlonym ciałem.

I w tym przypadku Grimaldi był w stanie zaobserwować zjawisko, które później nazwano "dyfrakcją Fresnela", w wyniku czego na ekranie uzyskano obraz dyfrakcyjny przeszkody. Analitycznie obliczyć, jest to bardzo trudne. Istnieją jednak metody, które pozwalają w niektórych szczególnych przypadkach znacznie uprościć te obliczenia.

I jeszcze jedna uwaga na temat eksperymentów Grimaldi. Gdyby użył okrągłej tarczy (na przykład spodka) jako ekranu w nich, być może byłby w stanie obserwować coś takiego jak dyfrakcja Fresnela na okrągłym dysku półtora wieku wcześniej niż to miało miejsce. Ale historia w ogóle, a historia nauki w szczególności nie wiem. tryb łączny. Dlatego eksperyment ten przeprowadzono tylko na początku 19 wieku. (patrz poniżej).

Pierwsza obserwacja interferencji

Pomijanie promienie słoneczne do pokoju przez kilka małych okrągłych otworów, Grimaldi otrzymał ślady nakładających się stożków światła na ekranie. Jak można się było spodziewać, w obszarach, w których padały promienie z dwóch dziur, ekran był oświetlony bardziej niż z jednego stożka światła; ale badacz z zaskoczeniem odkrył, że te części całego cienia, w których stożki światła nakładały się na siebie, okazały się ciemniejsze niż odpowiadające im części, w których nie było nakładki (rysunek poniżej). 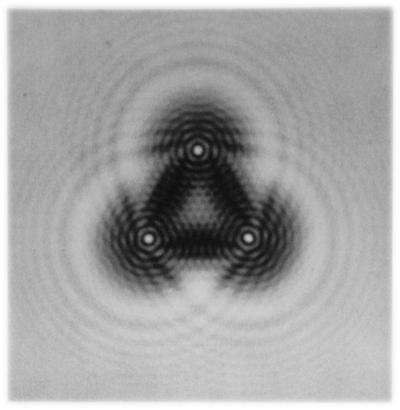Tak więc po raz pierwszy odnotowano, że oświetlony korpus może stać się ciemniejszy, jeśli dodamy światło do tego, który już otrzymuje. Teraz wiemy, że przyczyną tego są zakłócenia, tj. Wzajemne wzmocnienie lub osłabienie fal świetlnych. Przejawia się również w takim zjawisku jak dyfrakcja Fresnela. Wielu współczesnych naukowców nawet nie różnicuje zasadniczo tych pojęć, redukując wszystkie manifestacje dyfrakcyjne do manifestacji interferencji, jak na przykład R. Feynman w 3 tomie jego "Wykładów Feynmana o fizyce".

Od Grimaldi do Huygensa i Newtona

Pierwszą próbę wyjaśnienia przyczyny odchylenia światła od propagacji prostoliniowej dokonał słynny angielski naukowiec R. Guk. Zasugerował, że światło jest oscylacjami fali eteru światowego, który wówczas był rozumiany jako wszechprzenikająca substancja, która wypełnia całą przestrzeń. Pomysł Hooke'a już położył fundament pod przyszłe poprawne wyjaśnienie, czym jest dyfrakcja Fresnela i wszystkie zjawiska optyczne. Nie był jednak w stanie stworzyć odpowiedniej teorii ilościowej.

Następnym krokiem był Christian Huyges, który sformułował swoją słynną zasadę w 1690 roku. Według niego światło widzialne to zbiór sferycznych fal propagujących się od źródła we wszystkich kierunkach w eterze. W tym przypadku źródłem tych fal mogą być nie tylko cząstki eteru wzbudzone bezpośrednio przez źródło światła (na przykład płomień świecy), ale także dowolne inne jego cząstki w punktach w przestrzeni, które światło przechodzi podczas propagacji. Powstająca fala widzialna jest w dowolnym momencie kopertą wszystkich fal wtórnych. Ta ostatnia może dobrze rozprzestrzeniać się poza granice przeszkód na ścieżce światła, która jest dobrze nałożona na obrazy ich cieni obserwowanych podczas dyfrakcji. Dlatego, zgodnie z tą teorią, po prostu nie ma przeszkody wokół światła - z nowych (wtórnych) źródeł wykracza poza przeszkody.

Jednak zgodnie z zasadą Huygensa, wąskie promienie światła są w ogóle niemożliwe - ich krawędzie powinny natychmiast rozprzestrzeniać się we wszystkich kierunkach. Można je jednak zobaczyć gołym okiem, tak jak to było w przypadku eksperymentów Grimaldiego. Występowała sprzeczność między teorią a praktyką.

I. Newton próbował przezwyciężyć to w swojej korpuskularnej teorii światła, która również wyjaśniła wszystkie zjawiska optyczne, w tym takie jak dyfrakcja światła Fresnela. Jednak główny postulat Newtona, że ​​światło nie jest falą w powietrzu, ale strumieniem ciał (ciałek), dał początek innym sprzecznościom. Tak więc nie było jasne, dlaczego przecinające się wiązki światła nie wpływają na siebie nawzajem, ponieważ ciałka musiałyby kolidować ze sobą. Ale autorytet Newtona był tak wysoki, że falowa teoria światła została zapomniana przez ponad sto lat.

Powracają fale świetlne

W 1880 angielski fizyk T. Jung zaproponował powrót do falowej teorii światła, uzupełnionej koncepcją interferencji fal świetlnych. Oznacza to, że gdy koherentne (przy identycznych częstotliwościach) fale nakładają się na siebie, intensywność czasu natężenia światła w niektórych punktach pola i tłumienie w innych, w zależności od stosunku fazowego dodawanych fal świetlnych, jest stabilna.

Pojęcie interferencji wykorzystał francuski fizyk O. Fresnel, aby uzupełnić je zasadą Huygensa. Według jego wariantu, wszystkie drugorzędne fale sferyczne są spójne i przeszkadzają w nakładaniu. Jaki jest fizyczny mechanizm dyfrakcji Huygensa-Fresnela?

Przepuszczanie światła przez okrągły otwór

Gdy fala świetlna rozprzestrzenia się przez otwór, zależność pomiędzy jej średnicą a długością fali padającej wiązki określa zachowanie światła. Jak pokazano po lewej stronie poniższego rysunku, gdy długość fali jest znacznie mniejsza niż średnica otworu, po prostu przechodzi ona do przodu w linii prostej, tak jakby w ogóle nie było przeszkód.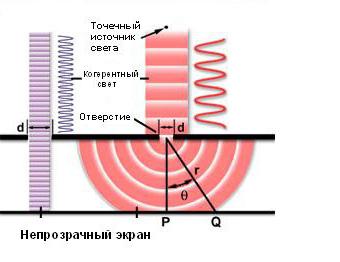

Z prawej strony figury pokazano jednak inną sytuację. W tym przypadku długość fali światła przesyłanego ze źródła punktowego przekracza średnicę otworu, a na aperturze występuje dyfrakcja Fresnela. Analizując to zjawisko, dziurę uważa się za nieobecną, a zamiast niej umieszcza się zestaw fikcyjnych źródeł światła wtórnego, które wzbudzają te same drugorzędne fale sferyczne, które zostały już wspomniane powyżej. Rozchodzą się w kierunku ekranu i docierają do różnych punktów o różnych fazach, przeszkadzając sobie nawzajem, to jest zwiększając lub osłabiając w każdym z takich punktów. Ponieważ cały system ma symetria osiowa, następnie padająca cylindryczna wiązka światła zamienia się w stożkowy, a na ekranie znajduje się również osiowo-symetryczny wzór dyfrakcyjny naprzemiennych jasnych i ciemnych pierścieni, zwany także odpowiednio maksimami i minimami oświetlenia. W punkcie P, znajdującym się na osi otworu, pojawi się jasna plama - główne maksimum, a pierwsze z wtórnych maksimów oświetlenia wystąpią w punkcie Q. Natężenie maksimów wtórnych maleje wraz ze wzrostem odległości od środka wzoru dyfrakcji. Stosunek wielkości otworu do stopnia ugięcia określa następujący równanie:

sinθ = λ / d, gdzie

• θ jest kątem między kierunkiem do środka wzoru dyfrakcyjnego a kierunkiem do jego pierwszego minimum,
• λ jest długością fali światła.

Poniższy rysunek pokazuje, jak intensywność luminancji ekranu zmienia się w zależności od odległości kątowej od środka. Zauważ, że minima między drugorzędnymi maksimami są umiejscowione w punktach wielokrotności Π.

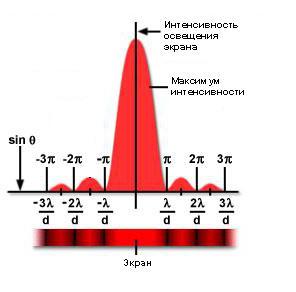
Analityczne obliczenia obrazu takiego zjawiska, jak dyfrakcja Fresnela na otworze i dysku, są znacznie uproszczone dzięki osiowej symetrii, co zostanie omówione dalej.

Okrągły dysk na drodze wiązki światła

Jeśli będziemy postępować zgodnie z teorią Fresnela, to gdy okrągły promień zostanie umieszczony na wiązce światła, wszystkie punkty na jej krawędziach staną się źródłami spójnych wtórnych sferycznych fal. Odległości między tymi punktami a punktem przecięcia osi dysku z nieprzezroczystym ekranem prostopadłym do niego są takie same. Dlatego fale ze wszystkich punktów na krawędzi dysku muszą przecinać się w tym samym czasie i w tej samej fazie, tj. Muszą być złożone i znacząco wzmacniać się nawzajem. Okazuje się, że pośrodku okrągłego cienia z tarczy należy obserwować jasny, oświetlony punkt, jak na poniższym rysunku. 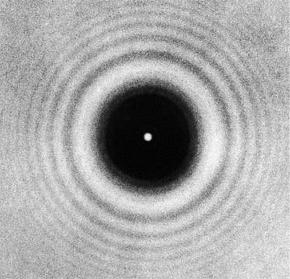Ta okoliczność została po raz pierwszy zauważona przez francuskiego fizyka S. Poissona, który był przeciwnikiem teorii Fresnela. Uznał, że okoliczność, którą zauważył, dowodzi jego niekonsekwencji. Jakie było jego zdziwienie, gdy Fresnel wraz z Arago zrobili odpowiednie doświadczenie i dostali takie miejsce w centrum cienia z dysku! Poniższy rysunek schematycznie pokazuje to doświadczenie.

W ten sposób dyfrakcja Fresnela manifestuje się na dysku. Jasne miejsce pośrodku jego cienia otrzymało nazwę miejsca Poissona. Jeśli dysk jest mały, natężenie światła w środku jego obrazu dyfrakcyjnego jest prawie takie samo jak w przypadku jego braku (dysku).

Jak obliczyć wzory dyfrakcji

W ogólnym przypadku obliczenie interferencji fal drugorzędnych w celu uzyskania dyfraktogramu jest trudne. Ale w przypadkach osiowosymetrycznych można go uprościć, aby cały obraz zjawiska dyfrakcji stał się prosty. Metoda stref Fresnela pozwala wizualnie geometrycznie przełamać przód fali sferycznej na sekcje okrągłe.

Amplitudy i względne fazy wszystkich stref są brane pod uwagę przy obliczaniu rozkładu intensywności. W związku z tym do określenia wzoru dyfrakcji stosuje się dość złożone przetwarzanie matematyczne. Ale analizując takie zjawisko, jak dyfrakcję Fresnela na okrągłym otworze i dysku, jest znacznie uproszczony.

Na poniższym rysunku S jest punktowym źródłem światła. 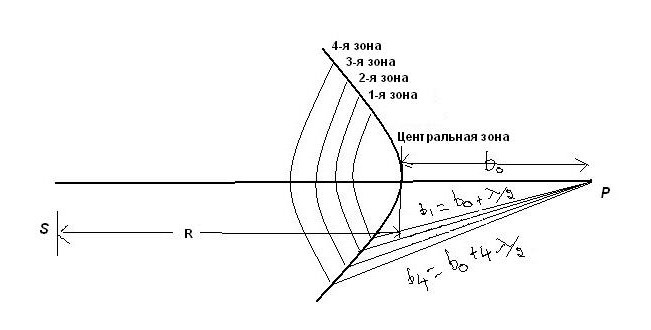S emituje sferyczną falę świetlną o długości λ w kierunku od lewej do prawej. Niech promień jego frontu w czasie t będzie równy R. Efekt tego czoła fali w punkcie P jest określony przez podzielenie go na pierścieniowe strefy. Odległości od krawędzi dwóch kolejnych stref do punktu P różnią się o λ / 2. Strefy pierścieniowe z tą właściwością nazywane są strefami Fresnela. Odległość od strefy zerowej do punktu P wynosi b ₀ .

Pierwsza strefa znajduje się w odległości b ₁ = b ₀ + λ / 2; drugi: b ₂ = b ₀ + 2λ / 2; trzecie: b ₃ = b ₀ + 3λ / 2; i-ta strefa: b _i = b ₀ + iλ / 2.

Kolejne krawędzie dwóch sąsiednich stref znajdują się w podobnych punktach. Jeśli wtórne fale sferyczne są w nich wzbudzane, wówczas dochodzą do punktu obserwacyjnego P z różnicą fazową 180 ° i wzajemnie się osłabiają, gdy nałożą się (ale nie zostaną zniszczone).

Dyfrakcja Fresnela na okrągłym otworze i dysku - obraz o osiowej symetrii. Dlatego zastosowanie tej metody pozwala znacznie uprościć konstrukcję obrazu dyfrakcyjnego, gdy światło przechodzi przez takie przeszkody.

W jaki sposób strefy pierścieniowe Fresnela działają na okrągłym otworze?

Rozważ ponownie przypadek, w którym dyfrakcja światła występuje w okrągłym otworze. Strefy Fresnela, w których można przełamać czoło fali, leżąc w otworze o danej średnicy przy określonej długości fali λ i odległości od przodu do ekranu b ₀ , mogą być wyrażone liczbą nieparzystą lub parzystą. Jak zauważono powyżej, fale wtórne z dwóch sąsiednich stref w każdym punkcie ekranu słabną, chociaż nie niszczą się nawzajem. Jeśli więc dla środka wzoru dyfrakcyjnego liczba stref Fresnela pasujących do otworu jest nieparzysta (2k + 1), wtedy amplituda oświetlenia w środku obrazu będzie sumą reszty pierwszej (centralnej) strefy i nieskompensowanego działania (2k + 1) - strefy, które będą się wzajemnie wzmacniać. Wzór dyfrakcji dla tego przypadku pokazano na poniższym rysunku.

Jeśli liczba stref Fresnela ustawionych w otworze jest równa, to wpływ wszystkich stref w środku obrazu będzie wzajemnie kompensowany parami i pojawi się w nim ciemna plama.