Wyższa matematyka: samolot w kosmosie
Drugim po linii prostej ważnym elementem geometrii przestrzennej jest płaszczyzna. Umiejętność opisania go za pomocą równania umożliwia obliczenie przestrzennych kątów i wysokości dla różnych trójwymiarowych kształtów. W tym artykule podajemy wszystkie rodzaje równań opisujących płaszczyznę w przestrzeni. Weź także pod uwagę możliwe opcje wzajemnego rozmieszczenia samolotów.
Geometryczna koncepcja samolotu
W geometrii dwuwymiarowej płaszczyzna nie jest rozpatrywana, ponieważ wszystkie problemy są rozwiązywane tylko we współrzędnych x i y. Kiedy dodamy trzecią oś współrzędnych z, płaszczyzna staje się ważnym elementem geometrycznym.
Określenie "płaszczyzna" jest rozumiane jako zbiór punktów, z których dowolne dwa, jeśli są połączone, otrzymany wektor zawsze będzie prostopadły do pewnego podanego wektora. Ten podany wektor nazywa się normalnym. Normalny odgrywa ważną rolę w numerycznym opisie płaszczyzny, a jego właściwości są wykorzystywane do rozwiązywania różnych problemów.
Poniższy rysunek pokazuje trzy płaszczyzny w przestrzeni (niebieskie), które przecina czwarta (czerwona).
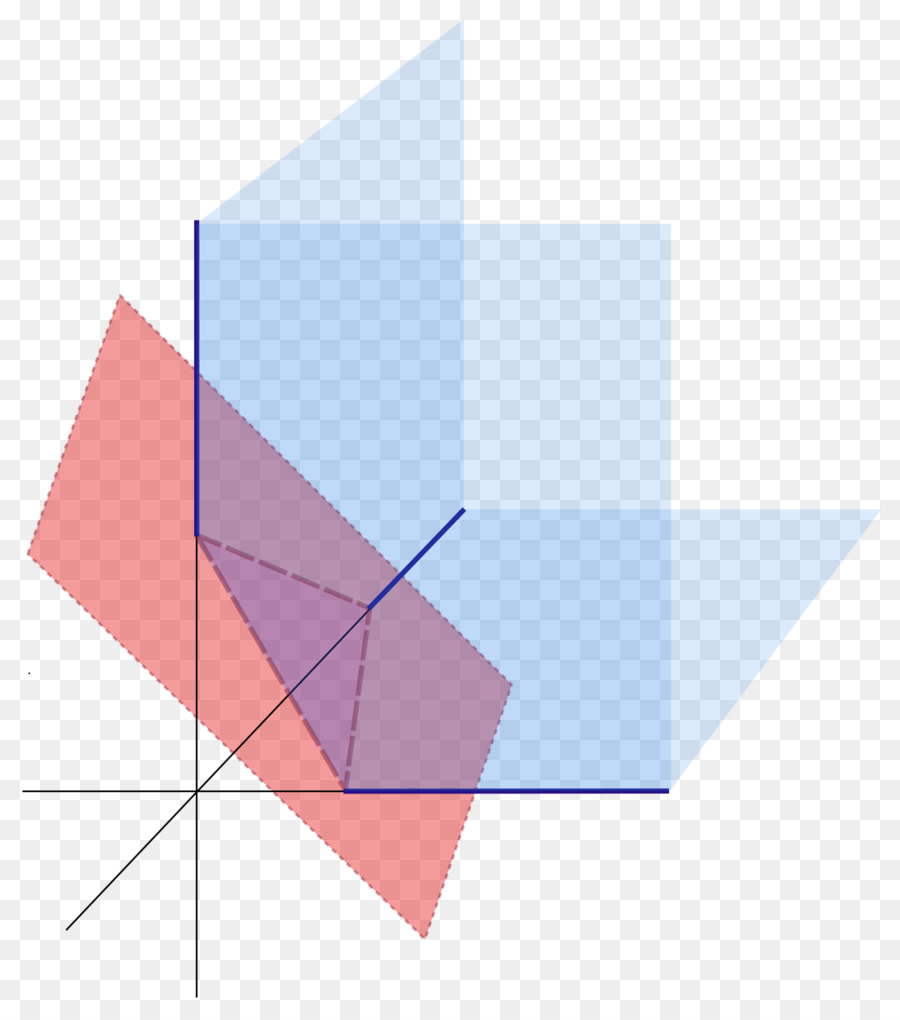
Ogólne równanie
Powyższa definicja pomoże uzyskać równanie płaszczyzny w przestrzeni we współrzędnych. Załóżmy, że istnieje punkt o znanych współrzędnych Q (x 0 ; y 0 ; z 0 ). Wiadomo, że leży ona w pewnej płaszczyźnie, której norma równa się n¯ (A, B, C). Załóżmy teraz, że dowolny punkt M (x; y; z) również należy do tej płaszczyzny. To ostatnie oznacza, że wektory QM¯ i n¯ będą prostopadłe, to znaczy, że ich iloczyn skalarny zniknie. Dlatego możemy napisać następującą równość:
(QM¯ * n¯) = 0.
Zastępując w nim współrzędne i otwierając nawiasy, dochodzimy do równania:
(xx 0 ) * A + (yy 0 ) * B + (zz 0 ) * C = 0 =>
A * x + B * y + C * z + D = 0, gdzie D = -1 * (A * x 0 + B * y 0 + C * z 0 ).
Wynikowe równanie dla płaszczyzny nazywa się ogólnym. Ma taką samą postać jak ogólne równanie bezpośredniego równania na płaszczyźnie. Można zauważyć, że współczynniki stojące przed zmiennymi x, yiz nie są niczym więcej niż współrzędnymi prostopadłej płaszczyzny wektora. Nazywa się reżyserią.
Zauważ, że jeśli podczas otrzymywania ogólnego równania konkretny punkt Q jest nieznany, a jest tylko wektor kierunkowy n¯, to docieramy do równania dla zestawu równoległych płaszczyzn, które różnią się tylko parametrem D.
Częściowe równanie
Przy przedstawianiu płaszczyzn w przestrzeni, gdy podano konkretne osie współrzędnych, najłatwiej jest zachować geometryczne konstrukcje, jeśli istnieją punkty, w których płaszczyzna przecina te osie. Wyrażenie, które pozwala ci znaleźć wartości współrzędnych przecięcia płaszczyzny z osiami x, yi z, nazywa się równaniem interwałowym. Można go uzyskać, wykonując niektóre przekształcenia matematyczne z ogólnym równaniem.
Załóżmy, że znane jest następujące równanie:
A * x + B * y + C * z + D = 0.
Przenieś wolny termin D na prawą stronę równania, a następnie podziel obie strony równania tak, aby jednostka znajdowała się po prawej stronie. Mamy:
A * x + B * y + C * z = -D =>
x / (- D / A) + y / (- D / B) + z / (- D / C) = 1 lub
x / p + y / q + z / r = 1, gdzie p = -D / A, q = -D / B, r = -D / C.
Wynikowe wyrażenie jest nazywane równaniem w segmentach, a długości segmentów, które są odcięte na osiach x, yi z, począwszy od punktu (0; 0; 0), mają odpowiednio wartości p, q i r. Można to sprawdzić w następujący sposób: jeśli założymy, że współrzędne wzdłuż osi y i z wynoszą zero, to x jest równe q. Oznacza to, że punkt przecięcia z osią X ma współrzędne (p; 0; 0). Podobnie, argumentując, otrzymujemy pozostałe dwie współrzędne (0; q; 0) i (0; 0; r).
Parametryczne równanie wektorowe
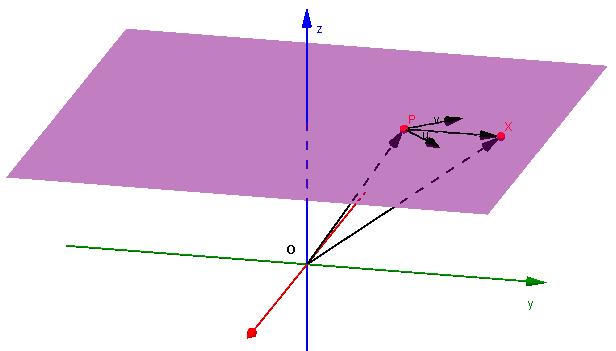
Jest to trzeci ważny typ równania, który jest często stosowany w rozwiązywaniu problemów. Powyżej pokazano, że płaszczyzna jest jednoznacznie określona przez punkt i wektor normalny. Jednak możliwe jest określenie tego geometrycznego obiektu dwuwymiarowego w inny sposób.
Załóżmy, że istnieją dwa współpłaszczyznowe wektory, które nie są do siebie równoległe. Oznaczamy je przez u¯ (a 1 ; b 1 ; c 1 ) i v¯ (a 2 ; b 2 ; c 2 ). Punkt Q (x 0 ; y 0 ; z 0 ) jest również znany. Jakie będzie równanie płaszczyzny przechodzącej przez ten punkt i dwa wektory?
Możesz odpowiedzieć na to pytanie, uzyskując ogólne równanie. Jednak rozwiążemy ten problem w inny sposób. Przypomnijmy, że każdy wektor płaszczyzny może zostać rozłożony na dwa inne współpłaszczyznowe wektory, które również należą do tej płaszczyzny. Oznacza to, że arbitralny wektor QP¯, gdzie P (x; y; z), może być reprezentowany jako:
QP¯ = α * u + + β * v¯.
Przebiegając przez wszystkie punkty P płaszczyzny, uzyskujemy odpowiednie parametry α i β. Równanie podane dla płaszczyzny nazywa się parametryczne wektorowe. Często jest zapisywany w formie współrzędnych:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + a * (a 1 ; b 1 ; c 1 ) + β * (a 2 ; b 2 ; c 2 ).
Można zauważyć, że ta forma zapisu płaszczyzny jest podobna do równania wektorowego dla prostej w dwuwymiarowych i trójwymiarowych przypadkach.
Wyrażenie to można również napisać bardziej wyraźnie, oddzielając zmienne:
x = x 0 + a * a 1 + p * a 2 ;
y = y 0 + α * b 1 + β * b 2 ;
z = z 0 + α * c 1 + β * c 2 .
Te trzy równania mają formę podobną do równania parametrycznego dla prostej w przestrzeni. Ten typ jest często używany podczas przekształcania równania wektora na typowy dla płaszczyzny.
Równoległe samoloty
Istnieją tylko dwie opcje względnej pozycji dwóch płaszczyzn w przestrzeni. W tej sekcji artykułu podajemy warunek, gdy są one równoległe.
Jeśli dwa równania płaszczyzny podane są w ogólnej formie, to ich równoległość jest dość prosta. Dwie płaszczyzny będą równoległe, jeśli ich wektory są takimi przewodnikami. Załóżmy, że istnieją dwa równania:
A 1 * x + B 1 * y + C 1 * z + D 1 = 0;
A 2 * x + B 2 * y + C 2 * z + D 2 = 0.
Prostopadle do każdej z płaszczyzn wektora są współrzędne:
n 1 ¯ (A1, B1, C 1 );
n 2 ¯ (A2, B2, C2).
Jeśli wektor n 1 ¯ może być reprezentowany przez mnożenie przez liczbę rzeczywistą wektora n 2 ¯, to oba z nich będą równoległe, czyli:
n 2 ¯ = l * n 1 ¯, gdzie l jest liczbą rzeczywistą.
Innym sposobem na ustalenie ich równoległości jest znalezienie cosinusa kąta między nimi poprzez iloczyn skalarny i moduły wektorów. Ten cosinus powinien być równy jedności, wtedy wektory (płaszczyzny) będą równoległe. Odpowiednia formuła to:
cos (φ) = | (n 1 ¯ * n 2 ¯) | / (| n 1 ¯ | * | n 2 ¯ |) = 1.
Jeśli równania płaszczyzn są podane w postaci parametrycznej wektorowej, to równoległość w przestrzeni płaszczyzn jest również określana na podstawie stanu równoległości normalnych do nich. Aby znaleźć kierunkowe wektory tych normalnych, należy pobrać produkty wektorowe wektorów tworzących każdą płaszczyznę.
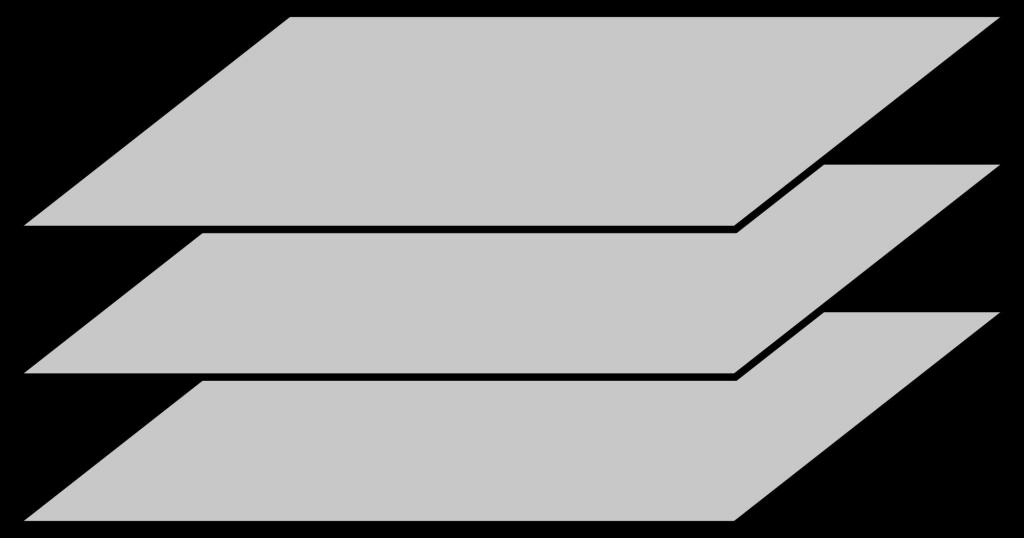
Powyższy rysunek pokazuje trzy płaszczyzny, które są do siebie równoległe.
Przecięcie płaszczyzn
Jest to druga wersja wzajemnego układu w przestrzeni samolotów. W takim przypadku dwie płaszczyzny przecinają się wzdłuż linii prostej, która do nich należy. W takim przypadku ważne jest, aby móc obliczyć kąt dwuścienny tego przecięcia. Jest zawsze równy kątowi pomiędzy odpowiednimi wektorami prowadzącymi, to jest między prostopadłymi płaszczyznami.
W poprzednim paragrafie podano już wzór, który umożliwia obliczenie kąta między normalnymi. Tutaj otworzymy go tylko pisząc współrzędne wektorów n 1 ¯ i n 2 ¯:
φ = arccos (| A 1 * A 2 + B 1 * B 2 + C 1 * C 2 | / (√ (A 1 2 + B 1 2 + C 1 2 ) * √ (A 2 2 + B 2 2 + C 2 2 ))).
Ta formuła jest często używana przy obliczaniu kątów dwuściennych między płaszczyznami piramidy lub nachylonego pryzmatu.
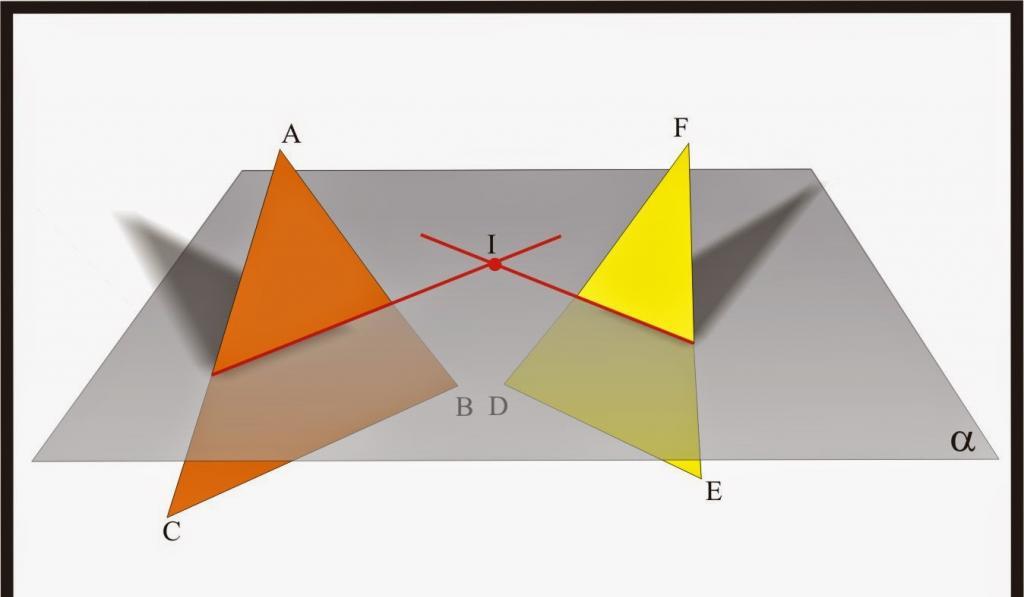
Dwie płaszczyzny przecinające trzeci poziom są pokazane na powyższym rysunku.
Szczególnym przypadkiem przecięcia się dwóch płaszczyzn jest kąt φ = 90 o , czyli jest prostopadłość rozpatrywanych obiektów geometrycznych. Aby określić prostopadłość, nie jest konieczne obliczanie kąta φ za pomocą nieco uciążliwej formuły powyżej, do tego wystarczy obliczenie wartości iloczynu skalarnego n 1 ¯ i n 2 ¯. W przypadku płaszczyzn prostopadłych jest to zero, to znaczy:
(n 1 ¯ * n 2 ¯) = A 1 * A 2 + B 1 * B 2 + C 1 * C 2 = 0.
Pakiet samolotów
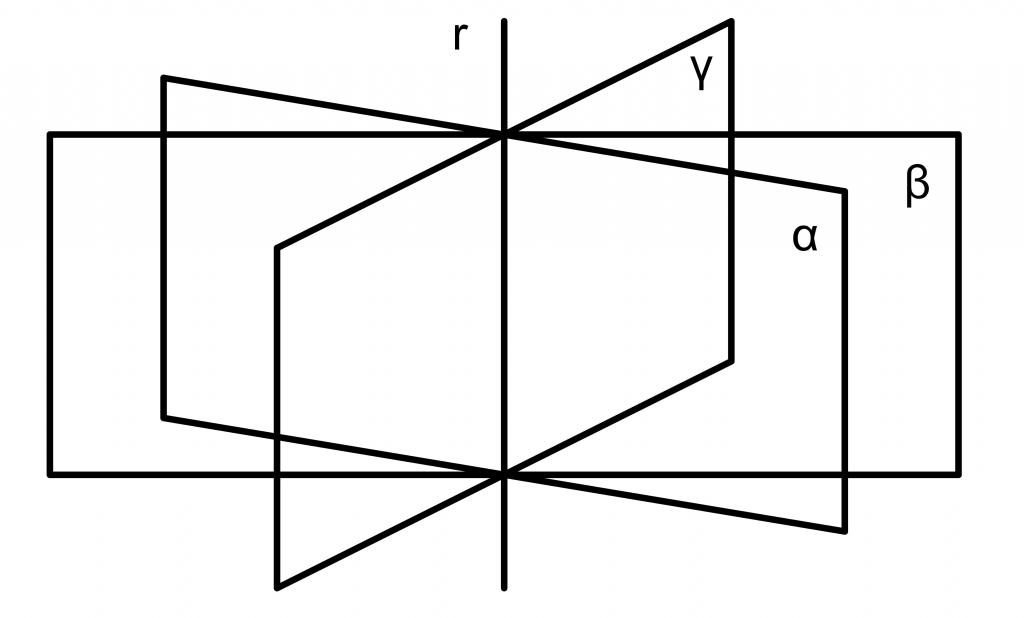
Jeśli dwa samoloty przecinają się, wszystkie ich wspólne punkty leżą na jednej linii prostej. Należy zauważyć, że jedną z metod określania linii prostej w kosmosie jest układ dwóch ogólnych równań płaszczyzny. Ile samolotów w kosmosie można przeciągnąć przez jedną linię prostą? Nieskończona liczba. Ich kolekcja nazywa się pakunkiem. Równanie opisujące ten pakiet ma następującą postać:
k 1 * (A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Tutaj k 1 i k 2 są liczbami arbitralnymi. Szczególnym przypadkiem jest sytuacja, gdy jeden lub oba parametry k nie mogą przyjąć wartości zero. Załóżmy, że k 1 ≠ 0, to równanie wiązki można przepisać w postaci:
(A 1 * x + B 1 * y + C 1 * z + D 1 ) + k 2 / k 1 * (A 2 * x + B 2 * y + C 2 * z + D 2 ) = 0.
Ta równość opisuje wszystkie płaszczyzny belki, z wyjątkiem tego, że ma się wektor bezpośredni n 2 ¯ (A2, B 2 , C 2 ).
Przykładem pakietu samolotów jest zbiór arkuszy otwartej książki.

Następnie rozwiązujemy kilka problemów geometrycznych, stosując uzyskaną wiedzę o właściwościach samolotów w przestrzeni.
Konwertuj parametryczne równanie wektorowe na ogólne
Biorąc pod uwagę następujące równanie płaszczyzny w postaci parametrycznej:
(x; y; z) = (1; 2; 0) + α * (1; 2; 3) + β * (- 1; 3; 0).
Konieczne jest zapisanie go jako ogólnego równania płaszczyzny w przestrzeni.
Zmieńmy to jawnie:
x = 1 + α - β;
y = 2 + 2 * a + 3 * p;
z = 3 * α.
Z ostatniego wyrażenia otrzymujemy α, a następnie podstawiamy je do pierwszej równości i wyrażamy β. Znalezione parametry są podstawione do drugiego równania, mamy:
α = z / 3;
β = 1 - x + z / 3;
y = 2 + 2 * z / 3 + 3 - 3 * x + z =>
y + 3 * x + 5/3 * z - 5 = 0 =>
9 * x + 3 * y + 5 * z -15 = 0.
Zatem, aby uzyskać ogólne równanie z wektora parametrycznego, musimy najpierw napisać go jawnie, a następnie wyrazić parametry w postaci zmiennych współrzędnych.
Konwersja ogólnego na parametryczne równanie wektorowe
To zadanie jest całkowicie przeciwne do poprzedniego. Rozważ techniki, aby je rozwiązać.
Biorąc pod uwagę następujące równanie:
x-2 * y + 3 * z -1 = 0.
Na początek jedna współrzędna powinna być wyrażona w dwóch. Wyrażaj na przykład x:
x = 2 * y-3 * z +1.
Oznacza to, że każdy punkt o współrzędnych będzie należał do płaszczyzny:
(2 * y-3 * z +1; y; z).
Teraz przepisujemy tę współrzędną jako sumę trzech wektorów, pierwszy będzie zawierał tylko zmienną y, drugi tylko z, a trzeci będzie składał się wyłącznie z liczb. Mamy:
(x; y; z) = (2 * y, y; 0) + (-3 * z; 0; z) + (1; 0; 0).
Widać, że otwierając to równanie, uzyskujemy ogólne współrzędne dla punktu płaszczyzny. Teraz pozostaje tylko wyodrębnić zmienne w pierwszym i drugim wektorze i przedefiniować je za pomocą parametrów α i β. Otrzymujemy:
(x; y; z) = (1; 0; 0) + α * (2; 1; 0) + β * (- 3; 0; 1).
Otrzymaliśmy równanie w postaci parametrycznej wektorowej, podobnej do oryginalnej.
Obraz płaszczyzny w układzie współrzędnych
Zadanie jest następujące: zgodnie ze znanym równaniem, należy narysować płaszczyznę w przestrzeni. Odpowiadające równanie to:
3 * x - y -4 * z +5 = 0.
Aby zobrazować tę płaszczyznę, konieczne jest znalezienie punktów, w których przecina ona osie współrzędnych. Aby to zrobić, możesz uzyskać odpowiednie równanie w segmentach. Jednak w tym przypadku postępujemy inaczej: umieszczamy dwie współrzędne równe zeru i obliczamy trzecie. Mamy:
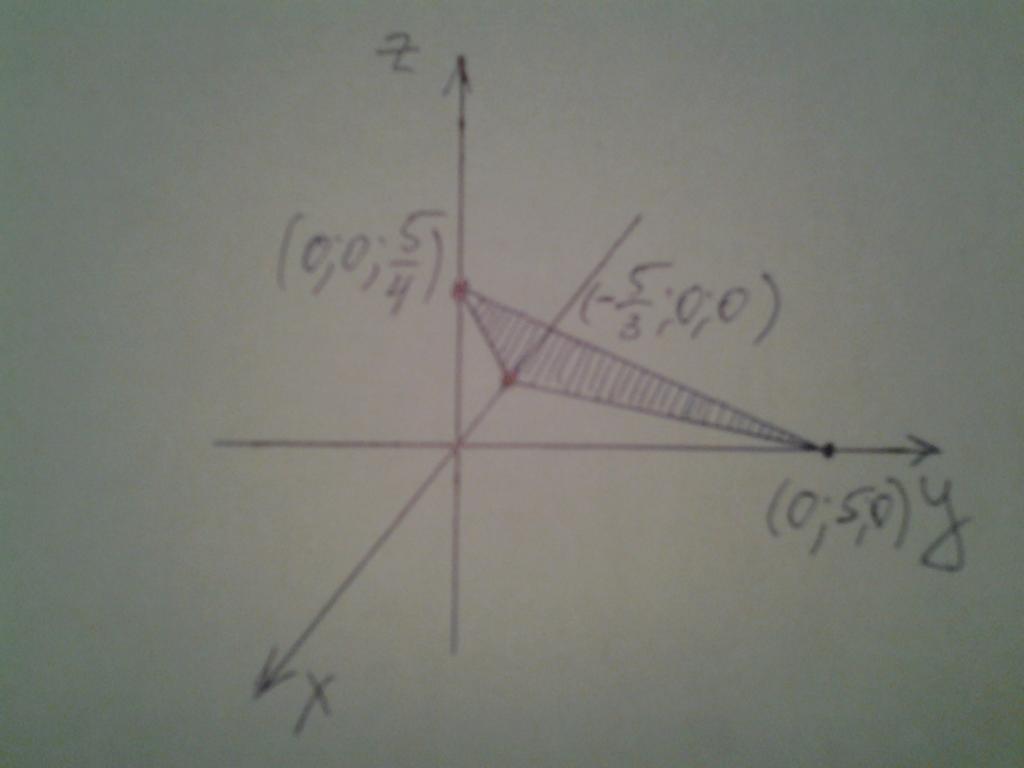
y = 0; z = 0; x = -5/3;
x = 0; z = 0; y = 5;
x = 0; y = 0; z = 5/4.
Pozostaje umieścić otrzymane punkty na osiach współrzędnych i narysować przez nie płaszczyznę. Położenie płaszczyzny w przestrzeni pokazano na poniższym rysunku.
Trzy punkty i samolot
Niech podane zostaną trzy punkty w przestrzeni:
M (1; -1; 3);
N (3; 2; 4);
L (2; 5; 0).
Konieczne jest znalezienie samolotu, który przez nie przechodzi.
Z geometrii wiadomo, że trzy punkty nie leżące na jednej linii prostej jednoznacznie określają płaszczyznę. Jego równanie można skomponować, jeśli znajdziemy jego wektor prowadzący n¯. Będzie równy wektorowi wektorów współpłaszczyznowych leżących w płaszczyźnie. Współrzędne wektorów można uzyskać ze współrzędnych punktów, na przykład:
MN¯ (2; 3; -7);
ML¯ (1; 6; -3).
Ich produkt wektorowy da wektor n¯. Obliczając to, otrzymujemy:
n¯ (33; -1; 9).
Biorąc na przykład punkt M, otrzymujemy ogólne równanie w postaci:
33 * x -y + 9 * z - 61 = 0.
Możesz zastąpić współrzędne punktów N i L równaniem i upewnić się, że zachowana jest równość.