Jak zbudować wykres funkcji liniowej. Przykłady
Aby dowiedzieć się, jak narysować funkcję liniową, ważne jest zrozumienie samej istoty tej funkcji. Funkcja jest modelem zależności zmian jednego parametru na drugim.
Temat zależności funkcjonalnych jest tradycyjnie otwarty z liniową zależnością funkcjonalną. Linear to najprostsza zależność. Wykres funkcji liniowej jest prosty.
Życie i funkcja
W życiu liniowe zależności zwykle znajdują się w idealnych sztucznych procesach, w których zakłada się, że zmiany są trwałe. Na przykład, gdy człowiek idzie gdzieś ze stałą prędkością.
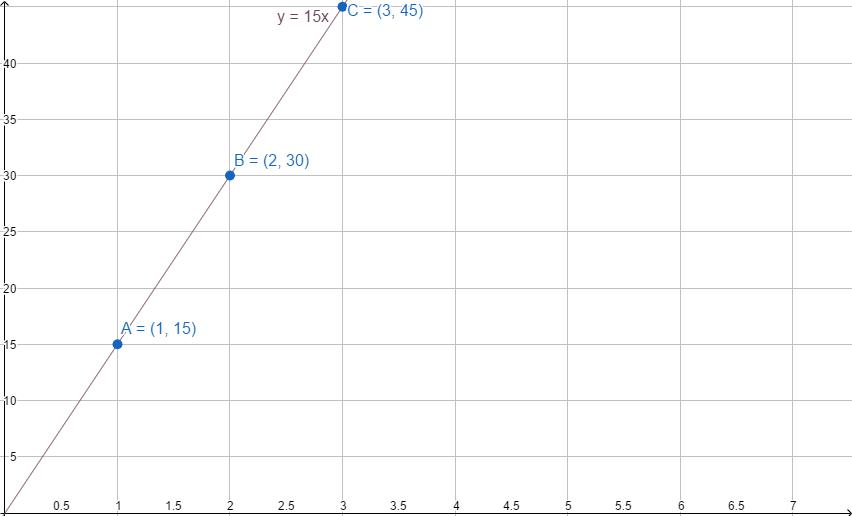
Odległość, jaką osoba będzie podróżować rowerem, będzie się zmieniać liniowo w zależności od liczby godzin, które podróżuje. Jeśli przejedzie 15 kilometrów na godzinę (punkt A), to za dwie godziny przejedzie 30 kilometrów (punkt B), w ciągu trzech godzin - 45 (punkt C).
Zależność opisana jest równaniem y = 15x. Jak narysować funkcję liniową w tym przypadku?
- znajdź współrzędne punktów, które są rozwiązaniem równania;
- zbuduj je na planie współrzędnych;
- połączyć te punkty z linią.
Opis algorytmu
Poszukiwanie współrzędnych punktów, które są rozwiązaniami równania, ogranicza się do znalezienia dwóch punktów, które jednoznacznie definiują linię. Chociaż wystarczy wybrać dwie różne wartości xi znaleźć odpowiednie wartości y, można znaleźć trzy pary wartości do samodzielnego sprawdzenia. Umożliwi to szybką identyfikację możliwego błędu w obliczeniach. Często pierwsza wartość x jest wybrana jako zero.
| y = 15x | (0, 0) | (1, 15) |
| x = 0 | x = 1 | |
| y = 15 × 0 | y = 15 × 1 | |
| y = 0 | y = 15 |
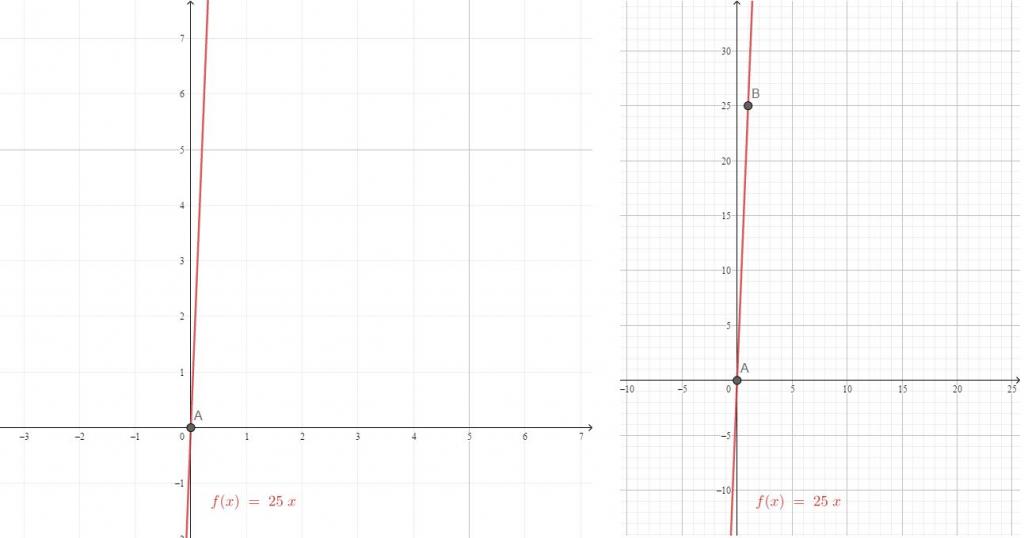
Druga wartość x dla dużego k jest lepsza do wyboru obok pierwszej. W przeciwnym razie wystąpi silne rozproszenie wartości y i x, na przykład przy x = 4 w rozpatrywanym równaniu, y = 60. W każdym razie, przed wykreśleniem funkcji liniowej na znalezionych punktach wybrana jest skala.
| y = 25 x | (0, 0) | (1, 25) |
| x = 0 | x = 1 | |
| y = 25 × 0 | y = 25 x 1 | |
| y = 0 | y = 25 |
Współczynnik dla x
Równanie funkcji liniowej ma postać y = kx + b. W zależności od zmiany współczynnika nieznanego zmienia się również charakter wykresu funkcji liniowej y = kx.
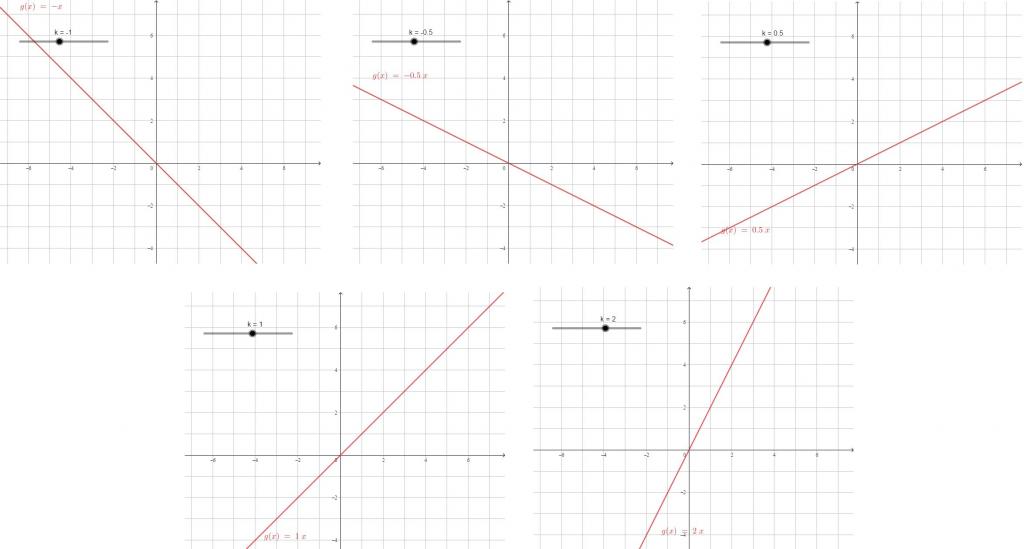
Im większy współczynnik modułu, tym większa jest stromość linii prostej, tym silniejsza dla tej samej zmiany wartości x wartości y zmieniają się. Współczynnik x jest współczynnikiem proporcjonalności.
Darmowy stosunek
Wolny współczynnik jest stałą, która nie zależy od zmian wartości x. Pokazuje, gdzie linia przecina się z OY.
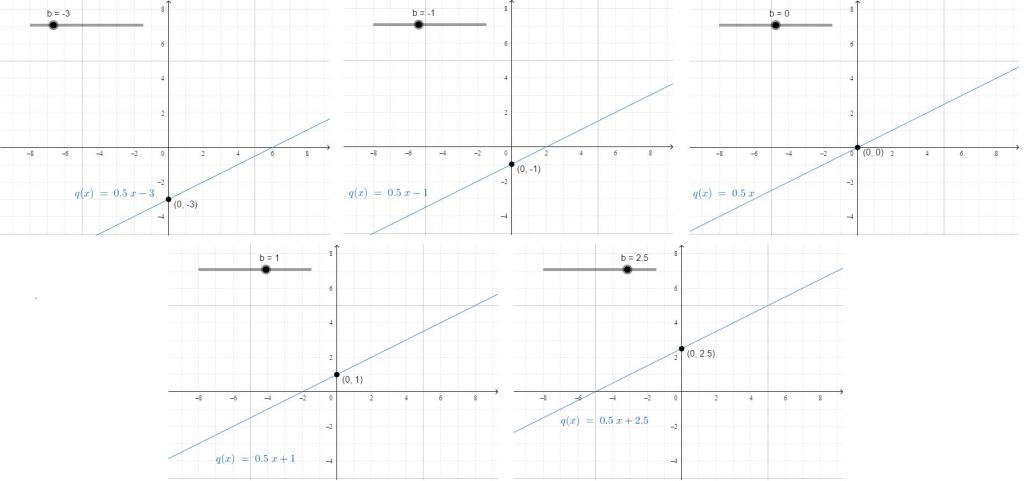
Na przykład człowiek przeszedł 10 kilometrów od rana do godziny 12 po południu, a następnie jeździł na rowerze przez trzy godziny. Następnie dystans, który pokonał na dzień: y = 15 × 3 + 10. Jeśli chcesz wyprowadzić wzór do obliczenia odległości na końcu każdej godziny z trzech, które jeździł na rowerze, możesz użyć: y = 15x + 10. O pierwszej W dniu, w którym przejechał 15 × 1, kolejne 10 minęło, o godzinie drugiej pojechał 15 × 2, ale przeszedł wszystkie 10 razy.
Wykres funkcji liniowej y = kx + b opisuje linię, która ma nachylenie k i przecina OY w punkcie o współrzędnych (0, b). Analiza równania często pozwala rozwiązywać problemy bez tworzenia wykresu. Ale aby działać w umyśle, działania muszą być dobrze związane z materiałem wizualnym.
Na przykład zadanie polega na znalezieniu punktów przecięcia y = - x 2 i y = 0,5x + 5. Pierwsza funkcja maleje, druga się zwiększa, pierwsza jest poniżej drugiej, ponieważ gałęzie paraboli są opuszczone, a jego wierzchołek jest na początku. Funkcja liniowa musiałaby mieć znacznie większy kąt nachylenia, aby była bardziej stroma i przekraczać jedną z gałęzi paraboli. Dlatego możliwe jest jednoznaczne określenie, że nie ma punktów przecięcia bez tworzenia wykresu i bez dokonywania podstawień.
Przypadki specjalne
- Gdy nie ma wolnego współczynnika, jest on (faktycznie) równy zeru, co oznacza, że linia prosta przecina się z OY na zero.
- Kiedy nie ma nieznanego x lub y, y i x są niezależne od siebie. Na przykład y = 5. Bez względu na to, jaką wartość przyjmuje x, y zawsze będzie 5. Graficznie, może być reprezentowana jako prosta równoległa do OX.
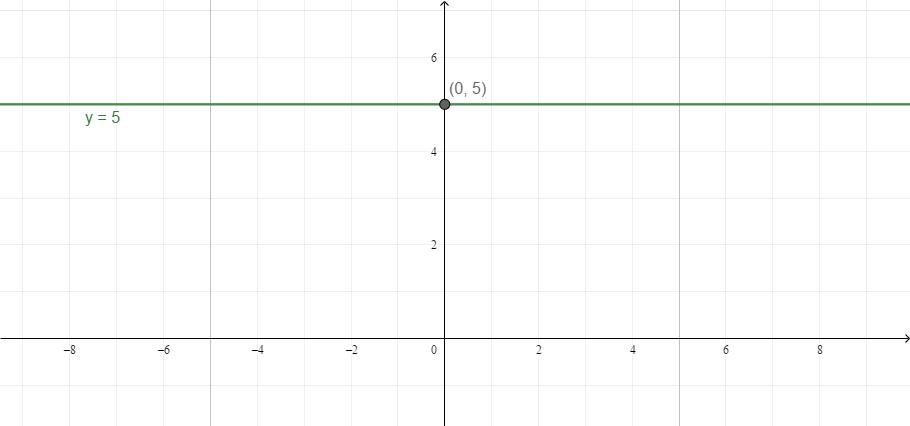
- To samo dotyczy przypadku, gdy zmienna x jest równa liczbie: zmienna x ma stałą wartość.
Analizując równanie jeszcze przed wykreśleniem funkcji liniowej, można ustalić jej przybliżoną lokalizację na OY i kąt nachylenia, a tym samym nachylenie. Pomaga to nie tylko znaleźć odpowiednią skalę i zbudować wykres, ale także rozwiązać niektóre problemy w umyśle.