Jak obliczyć kąty między linią a płaszczyzną?
Podczas studiowania szkolnego kursu geometrii w przestrzeni dwuwymiarowej poświęca się dużo czasu na rozważenie zachowania linii prostych. Kiedy przechodzą do badania stereometrii w wyższych klasach, na pierwszy plan wysuwają się motywy samolotów i proste linie w przestrzeni. W tym artykule omówiono jedno z tych pytań. Mianowicie, temat obliczeń między płaszczyznami a kątami prostymi i odległościami.
Prosta linia na płaszczyźnie i metody jej ustawiania
Aby skutecznie rozwiązywać problemy obliczeniowe między liniami prostymi a płaszczyznami kątów i odległości, konieczne jest nauczenie się matematycznego ustawiania tych obiektów geometrycznych, a także opanowanie metod pracy z odpowiednimi równaniami. Zaczynamy od określenia linii na płaszczyźnie.
Każdy uczeń zna następującą formułę:
y = k * x + b
Praca z nim jest wygodna w dwuwymiarowej przestrzeni. Jest łatwy w użyciu, aby narysować prostą linię w prostokątnym układzie współrzędnych. Ponadto, znajomość współczynnika k dla każdego z nich pozwala nam stwierdzić, czy będą one równoległe, czy też się przecinają (dla równoległości ich współczynniki k są równe).
Jeśli piszemy podane wyrażenie w nieco innej formie, to otrzymamy formułę ogólnego typu dla linii prostej. Jej forma jest następująca:
A * x + B * y + C = 0
Oczywiście, używając prostych transformacji, możesz uzyskać z niego pierwsze wyrażenie.
Zapisane formuły można również wykorzystać do obliczenia kąta przecięcia linii prostych. Wymaga to jednak wielu przekształceń, co jest niewygodne. Dlatego, gdy zadanie wymaga znalezienia kąta, lepiej jest użyć formy wektorowej reprezentacji linii. Jej widok można zapisać jako:
(x; y) = (x 0 ; y 0 ) + λ * (a; b)
W tej równości współrzędne X i Y z indeksami zerowymi opisują pozycję pewnego punktu, przez który przechodzi linia. Wartości a i b są współrzędnymi wektora leżącego na nim. Może być skierowany zarówno w jednym kierunku prosto, jak iw drugim, linia prosta się nie zmienia. Wektor ten nazywany jest wektorem prowadzącym, ponieważ jednoznacznie określa rozkład prostej na płaszczyźnie. Lambda λ to parametr, który przyjmuje dowolną wartość ze zbioru liczb rzeczywistych.
Zauważmy, że forma wektorowa rekordu jest godna uwagi, która wyraźnie zawiera skierowany odcinek linii prostej, którego współrzędne służą do określenia kąta między dwiema liniami prostymi na płaszczyźnie.
Prosta linia w trójwymiarowej przestrzeni
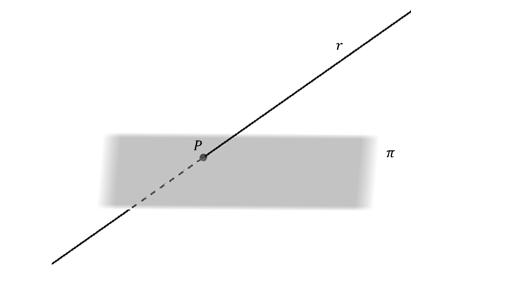
W przestrzeni opisanej przez trzy osie współrzędnych linia prosta jest określona w ogólnej formie jako przecięcie płaszczyzn. Tutaj, biorąc pod uwagę temat artykułu, rozważamy tylko równanie wektorowe. Jest podobny do płaskiego przypadku, ale z dodatkiem trzeciej współrzędnej:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a; b; c)
Podczas rozwiązywania problemów wyrażenie to jest wygodne do otwarcia i zastosowania w postaci parametrycznej:
x = x 0 + λ * a;
y = y 0 + λ * b;
z = z 0 + λ * c
Zauważ, że wartość parametru λ, choć dowolna, będzie zależna od wszystkich trzech równości.
Opis samolotu
Podobnie jak w przypadku linii prostej, w przypadku samolotu istnieje również wiele sposobów jego zdefiniowania. Rozważ tylko dwa z nich, które są ważne, aby wiedzieć, aby móc rozwiązywać problemy w praktyce.
Pierwszą metodą przypisania jest przedstawienie równania ogólnego typu. Jest podobny do odpowiedniego wyrażenia dla linii prostej w przypadku dwuwymiarowym:
A * x + B * y + C * z + D = 0
Kombinacja pierwszych trzech współczynników jest współrzędnymi wektora kierunku dla tej płaszczyzny. Z reguły jest oznaczony symbolem n¯, czyli:
n¯ = (A; B; C)
Czwarty współczynnik D określa odległość między równoległymi płaszczyznami mającymi pierwsze trzy identyczne współczynniki.
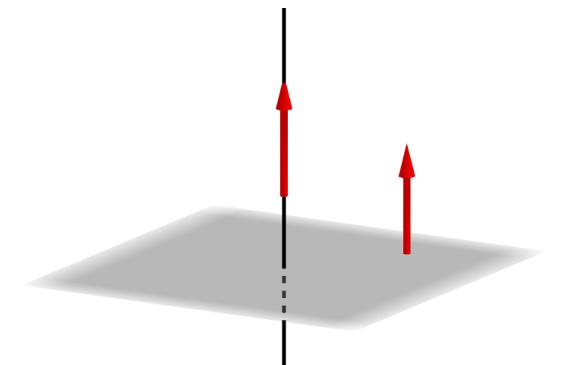
Ponieważ wektor n leży na normalnej płaszczyźnie, jest on prostopadły do absolutnie dowolnego wektora i linii prostej zbudowanej na jego dowolnych dwóch punktach. Znajomość współrzędnych n¯ jest kluczowa przy określaniu linii prostych i kątów.
Drugi sposób definiowania płaszczyzny jest wektorowo-parametryczną formą równania. Jest napisane w ten sposób:
(x; y; z) = (x 0 ; y 0 ; z 0 ) + λ * (a 1 ; b 1 ; c 1 ) + γ * (a 2 ; b 2 ; c 2 )
Ta równość odzwierciedla fakt, że dwie linie proste jednoznacznie definiują płaszczyznę w przestrzeni. Tutaj drugi i trzeci termin oznaczają dwa kierunkowe wektory dla dowolnych prostych linii należących do płaszczyzny.
Normalny wektor n¯ nie jest wyraźnie zawarty w tej formie pisania, ale łatwo jest go obliczyć:
n¯ = [(a 1 ; b 1 ; c 1 ) * (a 2 ; b 2 ; c 2 )]
Kąt między liniami prostymi
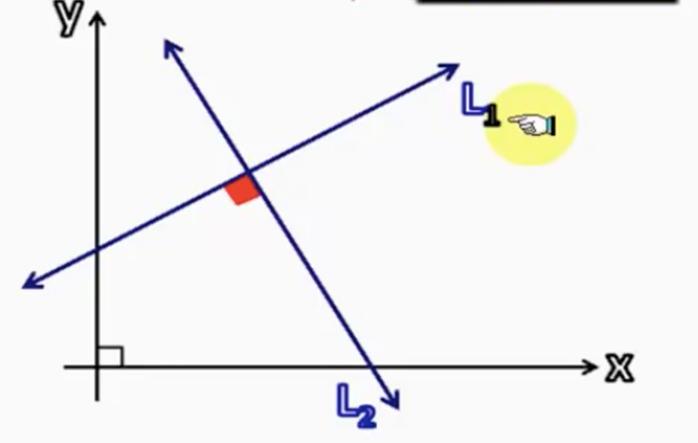
Jeśli wektor równości dla każdej linii prostej jest znany, kąt między nimi jest łatwy. Aby to zrobić, wystarczy użyć właściwości produktu skalarnego dla segmentów prowadzących linii prostych. Jeśli prowadnice wektorowe są oznaczone symbolami v¯ i u¯, wówczas wymagana formuła przyjmie postać:
α = arccos (| (v¯ * u¯) | / (| v¯ | * | u¯ |))
Ponieważ w przypadku przecięcia linii prostych powstają dwie pary równych kątów, wówczas jako kąt prawdziwy przyjmuje się kąt ostry. Z tego powodu formuła zawiera znak modułu w liczniku.
Ta formuła dla przypadku dwuwymiarowego jest zawsze ważna. Wynikowa wartość 0 o mówi, że linie proste nie przecinają się, ale są równoległe.
Jeśli chodzi o przypadek w przestrzeni, oprócz obliczeń za pomocą formuły, konieczne jest przeprowadzenie dodatkowych obliczeń. Są one powiązane ze znalezieniem punktu przecięcia przedmiotowych obiektów. Faktem jest, że w przestrzeni można uzyskać końcową wartość kąta α, ale linie proste nie przecinają się, ponieważ mogą się przecinać.
Płaszczyzna, linia i kąt ich przecięcia
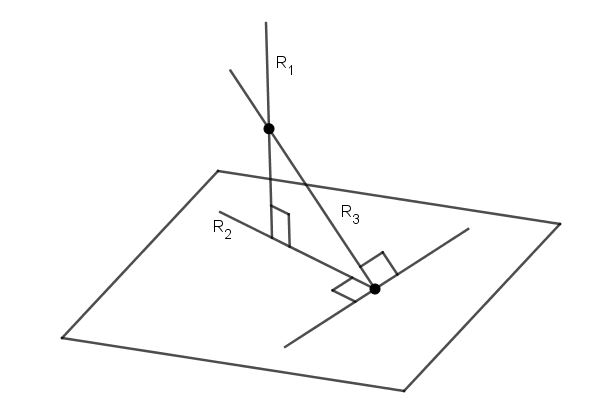
Aby znaleźć kąt między linią prostą a płaszczyzną, wystarczy znać równanie dla każdego z tych obiektów. Kąt między nimi to kąt dwóch przecinających się linii, z których jedna jest oryginalna, a druga należy do płaszczyzny i jest rzutem pierwotnej linii na nią. Poniższy rysunek pokazuje płaszczyznę, że linia prosta przecina się pod kątem α.
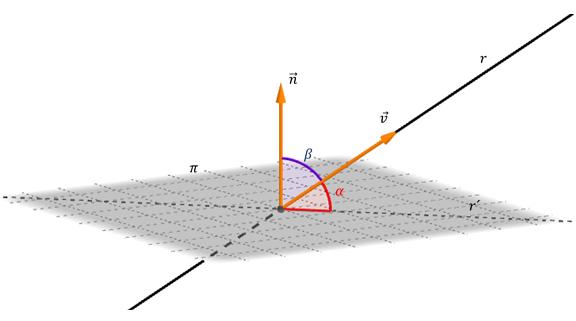
Jeśli wektor kierujący dla wektora bezpośredniego jest oznaczony przez v¯, a normalny do płaszczyzny to n¯ (patrz rys.), To obliczenie kąta α następuje za pomocą wzoru:
α = arcsin (| (v¯ * n¯) | / (| v¯ | * | n¯ |))
Należy zauważyć, że w tym wzorze, w przeciwieństwie do podobnego wyrażenia dla dwóch przecinających się linii prostych, używana jest funkcja arcus, a nie funkcja cosinus łukowy.
Odległość między liniami prostymi w płaszczyźnie i płaszczyźnie oraz prostą linią w przestrzeni
Aby obliczyć odległość między przedmiotami w geometrii, istnieje zestaw formuł. Zastosowanie wyrażenia z niego zależy od formy, w jakiej podana jest płaszczyzna i linia.
Jeśli dwie linie proste są podane w ogólnej formie na płaszczyźnie, wówczas odległość między nimi można obliczyć w następujący sposób:
d = | A * x 1 + B * y 1 + C | / √ (A 2 + B 2 )
Tutaj x 1 i y 1 są współrzędnymi dowolnego punktu na jednej linii prostej, a współczynniki A, B, C są przyjmowane dla drugiej linii prostej. Ta formuła jest poprawna, jeśli linie są równoległe do siebie. Jeśli się przecinają, odległość wynosi zero.
Odległość między linią a przecinającą ją płaszczyzną wynosi zero. Jeżeli linia prosta jest równoległa do płaszczyzny, wówczas odpowiadająca odległość jest obliczana jako:
d = | A * x 1 + B * y 1 + C * z 1 + D | / √ (A 2 + B 2 + C 2 )
Gdzie współrzędne należą do dowolnego punktu na linii.
Zadanie: ustal kąt między linią prostą a płaszczyzną
Biorąc pod uwagę linię prostą i samolot:
(x; y; z) = (1; 2; 0) + λ * (-1, 1; 4);
-5 * x + y - 3 = 0
Jaki jest kąt między linią prostą a płaszczyzną?
Piszemy przewodniki wektora v¯ i n¯:
v = (-1; 1; 4);
n¯ = (-5; 1; 0)
Zastąp je w odpowiedniej formule dla α, otrzymamy:
α = arcsin (| 5 + 1 + 0 | / (√18 * √26)) ≈ 16,1 o
Zadanie: znajdź odległość między liniami prostymi
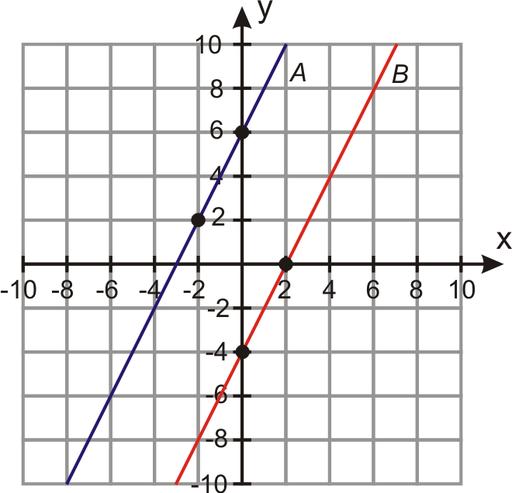
Biorąc pod uwagę dwa równania linii prostych w przestrzeni dwuwymiarowej:
y = 3 * x - 1;
y = 3 * x + 3
Jaka jest odległość między nimi?
Ponieważ współczynniki k dla obu obiektów są takie same (równe 3), ma miejsce przypadek równoległych linii prostych.
Aby obliczyć odległość między nimi, weź arbitralny punkt pierwszej linii prostej i przerób drugie równanie w ogólności, mamy:
współrzędne punktu (0; -1);
3 * x - y + 3 = 0, czyli A = 3, B = -1, C = 3
Teraz te wartości można zastąpić odpowiednią formułą:
d = | 3 * 0 -1 * (- 1) + 3 | / √ (9 +1) = 4 / √10 ≈ 1,265
Odpowiedź jest odbierana w jednostkach tego układu współrzędnych.