Jak przeprowadzić podział instrumentów pochodnych?

Podczas pracy z funkcjami często trzeba brać pod uwagę ich specyfikę, dodawanie, mnożenie lub dzielenie instrumentów pochodnych. W ostatnim z działań najczęściej pojawiają się pytania od ucznia, więc ten aspekt powinien być bardziej szczegółowo rozpatrzony.

Prywatna pochodna

Kiedy dokonuje się podziału instrumentów pochodnych, wzór przekształcenia wygląda jak różnica pomiędzy pochodną licznika pomnożoną przez mianownik a pochodną mianownika pomnożoną przez licznik i podzieloną przez kwadrat mianownika. Należy pamiętać, że wartość w dolnej części ułamka nie może być równa zero. Przy rozwiązywaniu pierwszych przykładów przekształcenie pochodnej ilorazu często powoduje problem, dlatego najlepiej mieć tę formułę przed oczami:

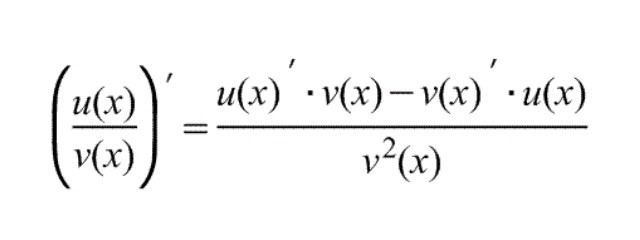
Dzięki tej formule można podać przykład w prostszej formie, którą można podzielić na tabularne funkcje pochodnych, po czym nie będzie trudno rozwiązać ten problem.

Przykład rozwiązania

Jako przykład pokazujący rozwiązanie, w którym dokonuje się podziału instrumentów pochodnych, warto rozważyć następujące kwestie:

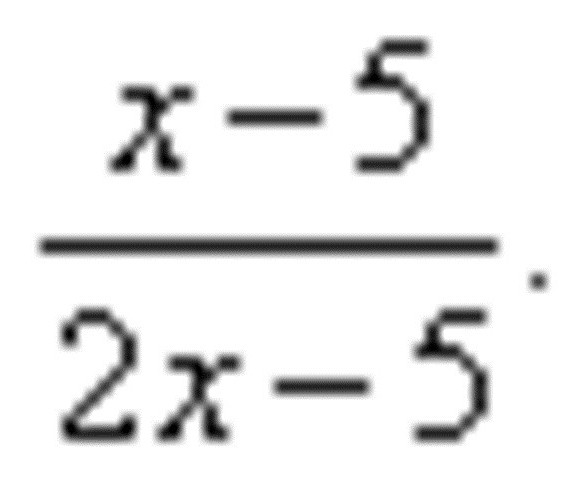
Zgodnie z zadaniem, konieczne jest znalezienie pochodnej tego wyrażenia. Korzystając z formuły, która upraszcza podział instrumentów pochodnych, przekształcamy oryginalny przykład w następujący sposób:

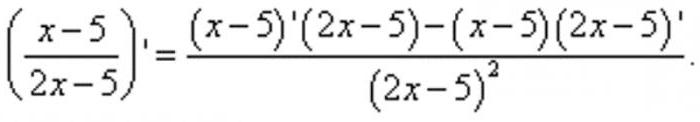
W rezultacie licznik okazał się być dwiema pochodnymi formularza tabelarycznego, których wartości można obliczyć bez dodatkowych konwersji. W pierwszym przypadku wynik będzie jeden, w drugim - dwa. Zastępując obliczone dane w przykładzie, uzyskujemy frakcję, w której pozostaje tylko wykonać proste obliczenia w liczniku, uzyskując wynik końcowy:

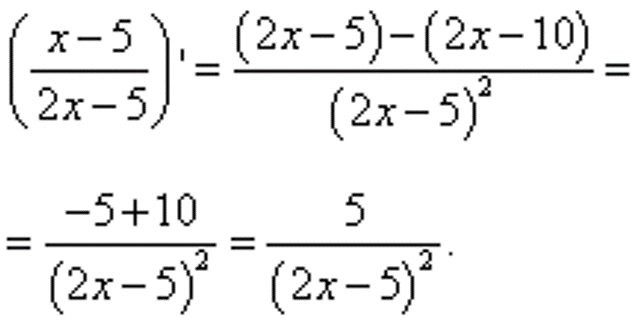
Małe sztuczki

Przed zastosowaniem formuły należy dokładnie przyjrzeć się podziałowi instrumentów pochodnych. W niektórych przypadkach ułamek można uprościć, tak aby formuła podana na początku mogła być niepotrzebna lub stała się prostsza. Ułamek można uprościć na kilka sposobów, w tym podzielić licznik za pomocą mianownika w celu określenia części całkowitej, a także pomnożyć obie części ułamka przez tę samą niezerową liczbę - ta technika jest często używana, gdy istnieje irracjonalność pod znakiem pochodnej.

Warto zauważyć, że najpierw trzeba sprawdzić przykład rozwiązania. Aby to zrobić, musisz znaleźć region wartości dopuszczalnych (DHS), a jeśli istnieje bez tworzenia niepewności innego typu, możesz przystąpić do obliczeń.