Jak znaleźć długość łuku koła

Wzór na znalezienie długości łuku koła jest dość prosty i bardzo często na ważnych egzaminach, takich jak badanie stanu jednolitego, występują takie problemy, których nie da się rozwiązać bez jego zastosowania. Trzeba go również znać, aby przejść międzynarodowe, standaryzowane testy, takie jak SAT i inne.

Jaka jest długość łuku koła?

Wzór jest następujący:

l = πrα / 180 °

Co to jest każdy z elementów formuły:

• l jest długością łuku koła;
• π jest liczbą pi (stała wartość równa ≈ 3,14);
• r jest promieniem danego koła;
• α to wartość kąta, na którym spoczywa łuk (raczej centralny niż wpisany).

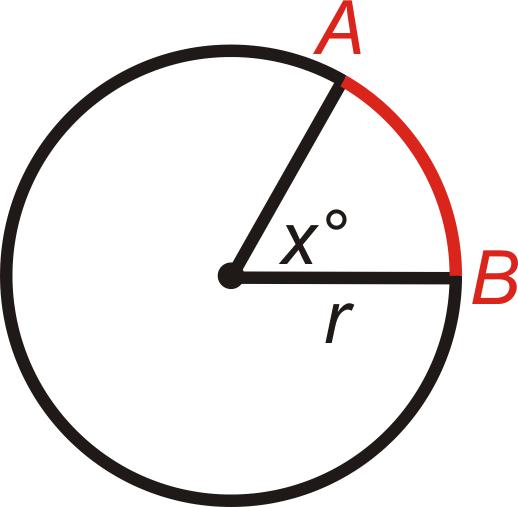
Jak widać, aby rozwiązać problem, warunek musi zawierać r i α. Bez tych dwóch wartości nie można znaleźć długości łuku.

Jak wyprowadza się tę formułę i dlaczego tak wygląda?

Wszystko jest niezwykle łatwe. Stanie się o wiele jaśniejsze, jeśli umieścisz 360 ° w mianowniku i dodasz dwójkę w liczniku z przodu. Możesz także not nie pozostawić ułamka, wycofać go i pisać ze znakiem mnożenia. Jest całkiem możliwe, aby stać, ponieważ ten element jest w liczniku. Następnie ogólny widok będzie:

l = (2πr / 360 °) × α

Dla wygody obniżono o 2 i 360 °. A teraz, jeśli przyjrzysz się uważnie, możesz zauważyć bardzo dobrze znaną formułę długości całego okręgu, a mianowicie 2πr. Całe koło składa się z 360 °, ponieważ dzielimy uzyskaną miarę na 360 części. Następnie pomnożymy przez liczbę α, czyli liczbę "kawałków ciasta", których potrzebujemy. Ale każdy wie na pewno, że liczba (czyli długość całego okręgu) nie może być dzielona przez stopnie. Co robić w tym przypadku? Zazwyczaj stopień jest z reguły zmniejszany o kąt środkowy, czyli z α. W końcu pozostają tylko liczby, a wynikiem jest ostateczna odpowiedź.

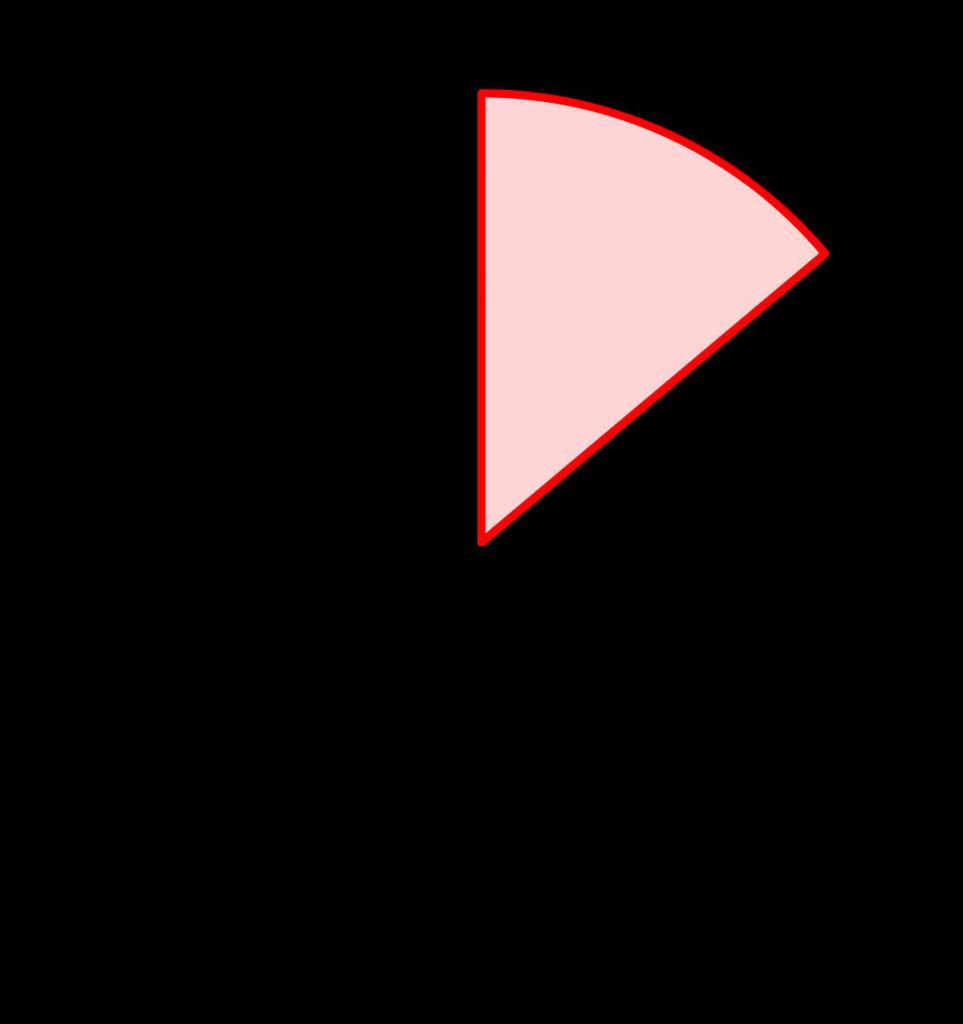
To może wyjaśniać, dlaczego długość łuku koła jest w ten sposób i ma tę formę.

Przykład problemu średniej złożoności za pomocą tej formuły

Stan: istnieje kółko o promieniu 10 centymetrów. Miara stopnia kąta środkowego wynosi 90 °. Znajdź długość łuku koła utworzonego przez ten kąt.

Rozwiązanie: l = 10π × 90 ° / 180 ° = 10π × 1/2 = 5π

Odpowiedź: l = 5π

Możliwe jest również, że zamiast miary stopni będą podawane miary kąta radianowego. W żadnym wypadku nie należy się obawiać, ponieważ tym razem zadanie stało się znacznie łatwiejsze. Aby zamienić radian na miarę stopnia, musisz pomnożyć tę liczbę przez 180 ° / π. Teraz możesz zastąpić następującą kombinację zamiast α : m × 180 ° / π. Gdzie m jest wartością radianu. A następnie 180 i liczba π są zredukowane i otrzymuje się całkowicie uproszczoną formułę, która wygląda następująco:

l = mr,

gdzie:

• l jest długością łuku koła;
• m jest radianową miarą kąta;
• r jest promieniem danego koła.