Jak znaleźć promień koła. Wpisane i ograniczone koło

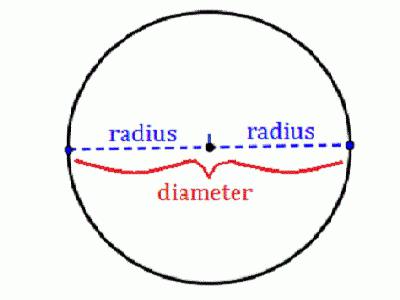
Promień jest segmentem, który łączy dowolny punkt na okręgu z jego środkiem. Jest to jedna z najważniejszych cech tej figury, ponieważ na jej podstawie można obliczyć wszystkie pozostałe parametry. Jeśli wiesz, jak znaleźć promień okręgu, możesz obliczyć jego średnicę, długość i powierzchnię. W przypadku, gdy ta liczba jest wpisana lub opisana wokół innej, można rozwiązać wiele zadań. Dzisiaj zbadamy podstawowe formuły i cechy ich zastosowania.

Znane wartości

Jeśli wiesz, jak znaleźć promień okręgu, który zwykle jest oznaczony literą R, to można go obliczyć z jednej cechy. Te wartości obejmują:

• obwód (C);
• średnica (D) jest segmentem (a raczej akordem) przechodzącym przez punkt środkowy;
• obszar (S) - przestrzeń ograniczona do tej liczby.

Wzdłuż obwodu

Jeśli wartość C jest znana w problemie, to R = C / (2 * P). Ta formuła jest pochodną. Jeśli wiemy, co to jest długość obwodu to nie trzeba pamiętać. Załóżmy, że w problemie C = 20 m. Jak znaleźć promień okręgu w tym przypadku? Wystarczy zastąpić znaną wartość w powyższym wzorze. Zauważ, że w takich problemach znajomość liczby P. jest zawsze domniemana, dla wygody obliczeń przyjmujemy jej wartość jako 3,14. Rozwiązanie w tym przypadku jest następujące: zapisz, jakie wartości są podane, wyprowadź formułę i wykonaj obliczenia. W odpowiedzi piszemy, że promień wynosi 20 / (2 * 3,14) = 3,19 m. Ważne jest, aby nie zapomnieć o tym, co myśleliśmy i wspomnieliśmy o nazwie jednostek miary.

Według średnicy

Natychmiast podkreślamy, że jest to najprostszy typ problemu, który pyta, jak znaleźć promień koła. Jeśli uzyskasz taki przykład na kontroli, możesz być spokojny. Nie potrzebuje nawet kalkulatora! Jak już powiedzieliśmy, średnica jest segmentem lub, dokładniej, akordem, który przechodzi przez środek. Co więcej, wszystkie punkty koła są w równej odległości. Dlatego ten akord składa się z dwóch połówek. Każdy z nich jest promieniem, który wynika z definicji jako segment łączący punkt na okręgu i jego środek. Jeśli znana jest średnica problemu, to aby znaleźć promień, wystarczy podzielić tę wartość przez dwa. Wzór jest następujący: R = D / 2. Na przykład, jeśli średnica problemu wynosi 10 m, wówczas promień wynosi 5 metrów.

Przez obszar koła

Ten typ zadania jest zwykle nazywany najtrudniejszym. Wynika to przede wszystkim z braku znajomości formuły. Jeśli wiesz, jak znaleźć promień okręgu w tym przypadku, reszta jest kwestią techniki. W kalkulatorze wystarczy wcześniej znaleźć ikonę pierwiastka kwadratowego. Obszar koła jest iloczynem liczby P i promienia pomnożonego przez siebie. Wzór jest następujący: S = P * R ² . Oddzielając promień po jednej stronie równania, możesz łatwo rozwiązać problem. Będzie równy pierwiastek kwadratowy od ilorazu powierzchni podzielonego przez liczbę P. Jeśli S = 10 m, to R = 1,78 metra. Podobnie jak w poprzednich zadaniach, ważne jest, aby nie zapominać o używanych jednostkach.

Jak znaleźć promień circumcircle

Załóżmy, że a, b, c są bokami trójkąta. Jeśli znasz ich wartości, możesz znaleźć promień okręgu opisanego wokół niego. Aby to zrobić, najpierw musisz znaleźć pół-obwód trójkąta. Aby ułatwić czytanie, oznaczmy to małą literą p. Będzie równa połowie liczby stron. Jego formuła to: p = (a + b + c) / 2.

Oblicz także iloczyn długości boków. Dla wygody oznaczamy go literą S. Formuła promienia opisanego koła będzie wyglądać następująco: R = S / (4 * √ (p * (p - a) * (p - b) * (p - c)).

Rozważ przykładowe zadanie. Mamy okrąg opisany wokół trójkąta. Długość jego boków to 5, 6 i 7 cm. Najpierw obliczamy pół-obwód. W naszym problemie będzie to 9 centymetrów. Teraz obliczamy iloczyn długości boków - 210. Podstawiamy wyniki obliczeń pośrednich do formuły i znajdujemy wynik. Promień wyznaczonego okręgu wynosi 3,57 centymetra. Zapisujemy odpowiedź, nie zapominając o jednostkach miary.

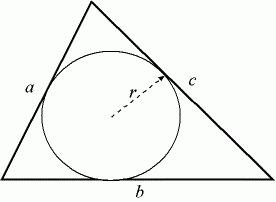
Jak znaleźć promień wpisanego koła

Załóżmy, że a, b, c są długością boków trójkąta. Jeśli znasz ich wartości, możesz znaleźć promień wpisanego koła. Najpierw musisz znaleźć jego pół-obwód. Dla ułatwienia zrozumienia oznaczamy to małą literą p. Wzór do obliczenia jest następujący: p = (a + b + c) / 2. Ten typ zadania jest nieco prostszy niż poprzedni, więc żadne pośrednie obliczenia nie są już potrzebne.

Promień wpisanego koła oblicza się za pomocą następującego wzoru: R = √ ((p - a) * (p - b) * (p - c) / p). Rozważ to na konkretnym przykładzie. Załóżmy, że problem opisuje trójkąt o bokach 5, 7 i 10 cm, w którym jest wpisane koło, którego promień znajduje się. Najpierw znajdujemy pół-obwód. W naszym problemie będzie to 11 cm, a teraz podstawiamy go do głównej formuły. Promień będzie równy 1,65 centymetrów. Zapisujemy odpowiedź i nie zapominamy o właściwych jednostkach.

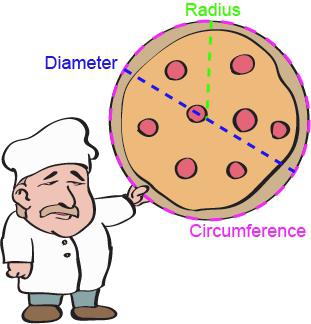
Okrąg i jego właściwości

Każdy geometryczny kształt ma swoją własną charakterystykę. Z ich zrozumienia wynika, że ​​poprawność rozwiązania problemów zależy. Mają krąg. Często są one używane do rozwiązywania przykładów z opisanymi lub wpisanymi liczbami, ponieważ dają one jasny obraz tej sytuacji. Wśród nich są:

• Linia prosta może mieć zero, jeden lub dwa punkty przecięcia z okręgiem. W pierwszym przypadku nie przecina się z nim, w drugim jest styczna, w trzecim - sieczna.
• Jeśli weźmiemy trzy punkty, które nie leżą na jednej linii prostej, to przez nie można narysować tylko jeden okrąg.
• Linia prosta może być styczną dwóch postaci naraz. W takim przypadku przejdzie przez punkt leżący na segmencie łączącym centra kół. Jego długość jest równa sumie promieni tych rysunków.
• Przez jeden lub dwa punkty możesz narysować nieskończoną liczbę okręgów.