Jak znaleźć pierwiastek kwadratowy? Właściwości, przykłady ekstrakcji rootów

Matematyka powstała, gdy człowiek się zrealizował i zaczął się pozycjonować jako autonomiczna jednostka świata. Pragnienie zmierzenia, porównania, obliczyć, co cię otacza - to było podstawą jednej z podstawowych nauk naszych czasów. Na początku były to elementy elementarnej matematyki, które pozwalały nam na powiązanie liczb z ich fizyczną ekspresją, późniejsze wnioski zostały przedstawione jedynie teoretycznie (z racji ich abstrakcyjności), no cóż, po jakimś czasie, jak to ujął pewien naukowiec, "matematyka osiągnęła pułap złożoności, gdy zniknęła wszystkie liczby. " Pojęcie "pierwiastka kwadratowego" pojawiło się w czasie, gdy można go było łatwo poprzeć danymi empirycznymi, wykraczając poza płaszczyznę obliczeń.

Jak to się wszystko zaczęło

Pierwsza wzmianka o rdzeniu, która jest obecnie określana jako √, została zapisana w pismach babilońskich matematyków, którzy zainicjowali nowoczesną arytmetykę. Oczywiście wyglądały trochę jak obecna forma - naukowcy z tamtych lat początkowo używali nieporęcznych tabletek. Ale w drugim tysiącleciu pne. e. otrzymali przybliżoną formułę obliczeniową, która pokazała, jak wyodrębnić pierwiastek kwadratowy. Poniższe zdjęcie pokazuje kamień, na którym babilońscy naukowcy wyrzeźbili proces √2, i okazało się tak prawdziwe, że rozbieżności w odpowiedzi znaleziono tylko w dziesiątym miejscu po przecinku.

Ponadto użyto korzenia, jeśli trzeba było znaleźć bok trójkąta, pod warunkiem, że dwa pozostałe są znane. Cóż, decydując równania kwadratowe Od wydobycia root nie może nigdzie iść.

Wraz z dziełami babilońskimi przedmiot tego artykułu został również zbadany w chińskim dziele "Matematyka w dziewięciu książkach", a starożytni Grecy doszli do wniosku, że jakakolwiek liczba, z której nie wyrasta korzeń bez pozostałości, daje wynik nieracjonalny.

Pochodzenie tego terminu wiąże się z arabskim przedstawieniem liczby: starożytni uczeni wierzyli, że kwadrat dowolnej liczby rośnie z korzenia, jak roślina. W języku łacińskim słowo to brzmi jak radix (możesz wyśledzić wzór - wszystko, co ma ładunek znaczeniowy, jest zgodne, czy to rzodkiewka, czy korzenie radiculitis).

Naukowcy nowej generacji podchwycili ten pomysł, określając go jako Rx. Na przykład, w XV wieku, aby wskazać, że pierwiastek kwadratowy pochodzi z dowolnej liczby a, napisano R2a. Znany "tyk" √ pojawił się dopiero w XVII wieku dzięki Rene Descartes.

Nasze dni

Z punktu widzenia matematyki pierwiastek kwadratowy z y jest taką liczbą z, której kwadrat jest równy y. Innymi słowy, z ² = y jest równoważne √y = z. Definicja ta jest jednak istotna tylko dla podstawy arytmetycznej, ponieważ implikuje nieujemną wartość wyrażenia. Innymi słowy, √y = z, gdzie z jest większe lub równe 0.

Ogólnie rzecz biorąc, to, co służy do definiowania algebraicznego korzenia, wartość wyrażenia może być zarówno dodatnia, jak i ujemna. Tak więc, z uwagi na to, że z ² = yi (-z) ² = y, mamy: √y = ± z lub √y = | z |.

Ze względu na to, że miłość do matematyki z rozwojem nauki wzrosła tylko, istnieją różne przejawy uczucia do niej, nie wyrażone w suchych obliczeniach. Na przykład, na równi z tak zabawnymi zjawiskami, jak dzień Pi, obchodzone są święta pierwiastka kwadratowego. Są one oznaczone dziewięć razy na sto lat i są określane zgodnie z następującą zasadą: liczby, które oznaczają dzień i miesiąc w kolejności, muszą być pierwiastkiem kwadratowym roku. Następnym razem będziemy świętować to święto 4 kwietnia 2016 r.

Właściwości pierwiastka kwadratowego na polu R

1. Pierwiastek kwadratowy produktu jest równy iloczynowi pierwiastków kwadratowych, pod warunkiem, że wyrażenia radykalne są większe lub równe 0.
2. Podczas wznoszenia pierwiastka kwadratowego wystarczy podnieść do tej potęgi wyraz radykalny, pod warunkiem, że jest większy od zera.
3. Pierwiastek kwadratowy ułamka jest równy pierwiastkowi licznika podzielonemu przez pierwiastek z mianownika, pod warunkiem, że pierwiastek kwadratowy licznika jest większy lub równy 0, a pierwiastek kwadratowy mianownika jest znacznie większy niż 0.
4. Wyrażenie radykalne, jeśli jest większe od zera, można podzielić na kilka części, z których z kolei można wyodrębnić pierwiastek. Na przykład: √75 = √25 * 3 = 5√3.
5. Pod znakiem korzenia możesz wpisać dowolną liczbę, podnosząc ją w kwadracie. Na przykład: 5√8 = √25 * √8 = √200.

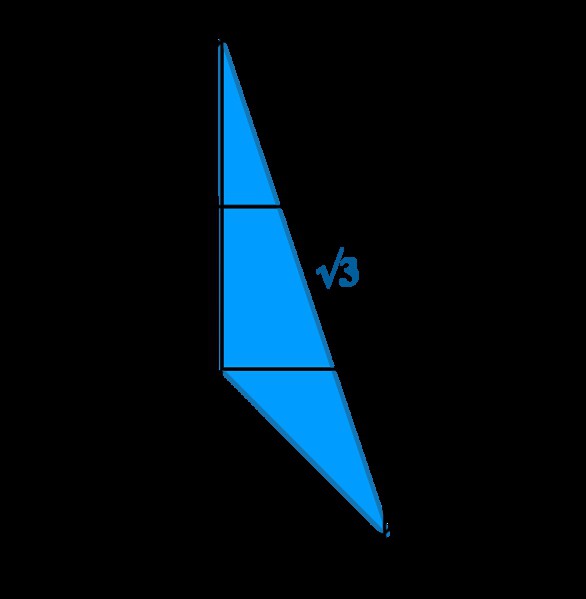
Praktycznie wszystkie wyrażenia matematyczne mają pod nimi geometryczną podstawę, a ten los i √y, który jest zdefiniowany jako bok kwadratu o polu y, nie uciekł.

Jak znaleźć źródło numeru?

Istnieje kilka algorytmów obliczeniowych. Najprostszym, ale raczej niewygodnym, jest zwykle obliczenie arytmetyczne, które składa się z następujących elementów:

1) od numeru, którego korzeń potrzebujemy, są odejmowane po kolei liczby nieparzyste - do momentu, gdy saldo wyjściowe będzie mniejsze niż odliczenie, a nawet zero. Liczba ruchów i ostatecznie będzie pożądaną liczbą. Na przykład, obliczając pierwiastek kwadratowy z 25:

25-1 = 24

24-3 = 21

21-5 = 17

17-7 = 10

10-9 = 1

Kolejna liczba nieparzysta to 11, reszta to: 1 <11. Liczba ruchów wynosi 5, więc korzeń 25 wynosi 5. Wszystko wydaje się łatwe i proste, ale wyobraź sobie, co musisz obliczyć z 18769? 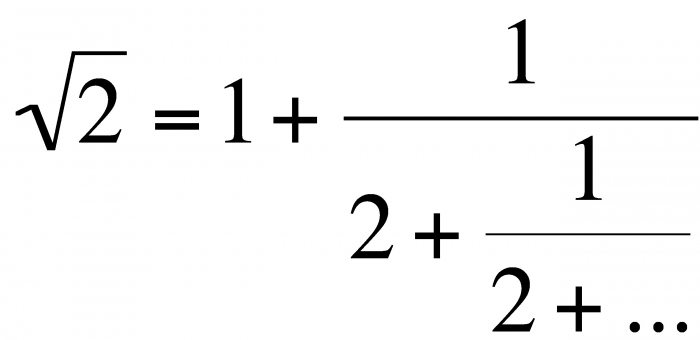W takich przypadkach w serii Taylora następuje dekompozycja:

√ (1 + y) = Σ ((- 1) ⁿ (2n)! / (1-2n) (n!) ² (4n)) y ⁿ , gdzie n przyjmuje wartości od 0 do

+ ∞ i | y | ≤1.

Graficzna reprezentacja funkcji z = √y

Rozważmy elementarną funkcję z = √y na polu liczb rzeczywistych R, gdzie y jest większe lub równe zeru. Jej harmonogram jest następujący: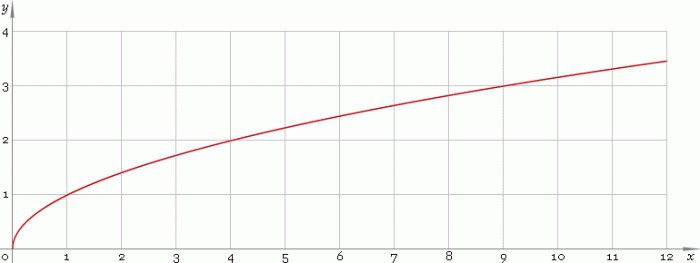

Krzywa rośnie od początku i niekoniecznie przecina punkt (1; 1).

Własności funkcji z = √y na polu liczb rzeczywistych R

1. Dziedziną rozważanej funkcji jest przedział od zera do plus nieskończoności (wliczono zero).

2. Zakres wartości danej funkcji jest przedziałem od zera do plus nieskończoności (zero jest włączone ponownie).

3. Minimalna wartość (0) funkcja przyjmuje tylko w punkcie (0; 0). Brak maksymalnej wartości.

4. Funkcja z = √y nie jest ani parzysta, ani nieparzysta.

5. Funkcja z = √y nie jest okresowa.

6. Punkt przecięcia wykresu funkcji z = √y z osiami współrzędnych jest tylko jeden: (0; 0).

7. Punkt przecięcia wykresu funkcji z = √y jest równy zeru tej funkcji.

8. Funkcja z = √y stale rośnie.

9. Funkcja z = √y przyjmuje tylko wartości dodatnie, dlatego jej wykres zajmuje pierwszy kąt współrzędnych.

Warianty funkcji obrazu z = √y

W matematyce, aby ułatwić obliczanie złożonych wyrażeń, czasami do napisania pierwiastka kwadratowego używana jest forma mocy: √y = y ^1/2 . Taka opcja jest wygodna, na przykład, w podnoszeniu funkcji do mocy: (√y) ⁴ = (y ^1/2 ) ⁴ = y ² . Ta metoda jest również dobrym pomysłem do różnicowania z integracją, ponieważ z tego powodu pierwiastek kwadratowy jest reprezentowany przez zwykłą funkcję mocy.

W programowaniu zastępowanie znaku is jest kombinacją liter sqrt. Należy zauważyć, że w tym obszarze pierwiastek kwadratowy jest bardzo poszukiwany, ponieważ jest częścią większości formuł geometrycznych potrzebnych do obliczeń. Sam algorytm obliczeniowy jest dość złożony i opiera się na rekurencji (funkcji, która sama się nazywa).

Pierwiastek kwadratowy w złożonym polu C

W zasadzie było to przedmiotem tego artykułu, który stymulował otwarcie pola. liczby zespolone C, ponieważ matematycy nie byli spokojni w kwestii uzyskania korzenia równego stopnia od liczby ujemnej. Tak więc pojawiła się wyimaginowana jednostka, która charakteryzuje się bardzo interesującą właściwością: jej kwadrat to -1. Dzięki temu równania kwadratowe i z ujemnym dyskryminatorem uzyskały rozwiązanie. W C, dla pierwiastka kwadratowego, istotne są te same właściwości, co w R, jedyne, co jest, to, że ograniczenia dotyczące radicand są usuwane.