Jak znaleźć objętość sześcianu: opcje problemów i ich rozwiązania
Nowoczesne technologie tworzą niesamowite programy komputerowe. Pozwalają zobaczyć objętość ciała i przekręcić je w różnych kierunkach, aby uzyskać lepszy wygląd. Wyobraźnia człowieka nie zawsze jest zdolna do tego. Niewiele osób może jasno przedstawić temat i zobaczyć go. Ale taką umiejętność można próbować formować przy rozwiązywaniu problemów w geometrii. Na przykład te, które mówią o tym, jak znaleźć objętość sześcianu. Jest to doskonała praktyka dla rozwoju wyobraźni przestrzennej.
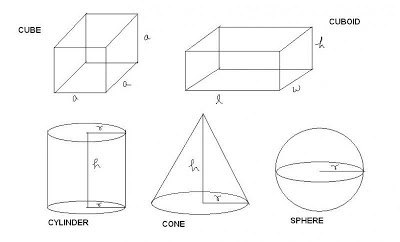
Kostka lub równoległościan?
To jest niepuste pytanie. Ponieważ klasyfikacja jest ważna. W końcu sześcian jest specjalną formą prostokątnego równoległościanu.
Ta ostatnia jest figurą, w której znajduje się 6 twarzy, a wszystkie z nich są prostokątami. Kąty, w których wszystkie krawędzie przecinają się, 90º. Odpowiednio, jeśli te ściany staną się kwadratami, wtedy cała figura zostanie przekształcona w sześcian.

W prostokątnym równoległościanie wszystkie wymiary liniowe, to znaczy wysokość, długość i szerokość, mogą się znacznie różnić. W sześcianie są one zawsze sobie równe. To jest jego znakiem rozpoznawczym. Dlatego w zadaniach wymagających znalezienia objętości kostki z pewnością brany jest pod uwagę rozważany moment. By the way, to znacznie upraszcza wszystkie zapisy matematyczne i obliczenia.
Konwencje w formułach i problemy
Bez tego elementu trudno będzie zrozumieć, w jaki sposób formuły są zapisywane. Znaczenie każdej litery i symbolu powoduje wyświetlenie poniższej tabeli.
| Symbol | Nazwa przedmiotu |
| a | kształt żebra |
| d | przekątna twarzy |
| D | przekątna sześcianu |
| wspólne symbole geometrii | kwadratowy |
| Tom |
Jak znaleźć elementy sześcianu na boku?
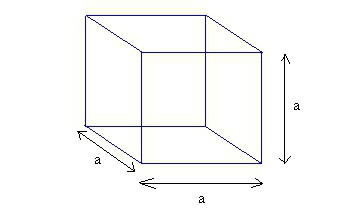
Ponieważ powierzchnia figury jest kwadratem, jej powierzchnię określa wzór nr 1, w którym znaną wartość należy podnieść do kwadratu:
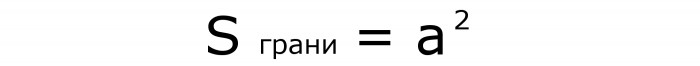
I przekątną dowolnej powierzchni oblicza się za pomocą wzoru nr 2, w którym strona jest pomnożona przez pierwiastek 2:
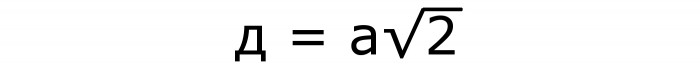
Poprzednia formuła została uzyskana z twierdzenia Pitagorasa. Jest to łatwe do zrozumienia, jeśli widzisz, że przekątna twarzy jest przeciwprostokątna trójkąt prostokątny. A boki kwadratu stają się jego nogami.
Aby określić przekątną sześcianu, potrzebna będzie następująca formuła nr 3, zawierająca znaną stronę i pierwiastek kwadratowy od 3:
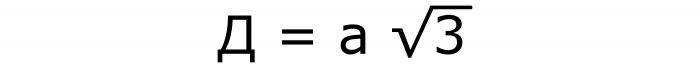
Jest również uzyskiwany z twierdzenia Pitagorasa. Tylko jako przeciwprostokątna działa pożądana przekątna. Bok kwadratu i jego przekątna stają się nogami.
Czasami musisz znać formułę, aby obliczyć powierzchnię boczną tej figury. W nim kwadrat boku jest pomnożony przez 4. Oto on (nr 4):
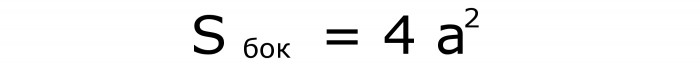
Zrozumienie, w jaki sposób działa ta formuła, jest łatwe. Są 4 powierzchnie boczne - 4. Oznacza to, że ich całkowita powierzchnia jest czterokrotnością wartości obszaru jednego kwadratu.
Jeśli chcesz określić obszar całej powierzchni , użyj tego rekordu, w którym kwadrat żebra jest zużyty (wzór nr 5):
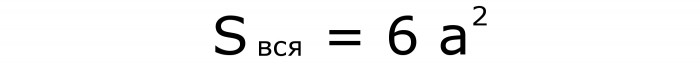
Uzyskano go podobnie jak w poprzedniej formule, tylko liczba kwadratów wzrosła do 6.
Czym jest objętość?
Mówiąc najprościej, jest to miejsce, które zajmuje ciało w przestrzeni. Każdy obiekt jest ograniczony przestrzenią przez powierzchnie. Może być ich kilka, ale mogą być przypadki, gdy tylko jeden. Na przykład, jeśli ciało jest kulą. Ale te powierzchnie są koniecznie zamknięte. Przestrzeń, jaką zajmuje ciało geometryczne, będzie jego pojemnością lub objętością.
Jednostki objętości
Jeśli chodzi o bryły, jednostkami objętości będą zawsze wartości sześcienne. Na przykład: metr, centymetr lub kilometr w sześcianie. W przypadku cieczy stosuje się litry wyrażone w decymetrach sześciennych. Ale jeśli zajmują bardzo duże objętości, mierzy się je również w metrach sześciennych. Na przykład biorąc pod uwagę zużycie wody w mieszkaniu, jest to rozważane wm 3 . Okazuje się więc wygodniejsze i łatwiejsze pod względem liczbowym.
Metoda 1: znajdź objętość kostki, jeśli znana strona
Jest to najłatwiejsza metoda informowania o tym, jak znaleźć objętość kostki. Po prostu podnosi wartość partii do trzeciego stopnia. Innymi słowy, musisz pomnożyć stronę trzy razy. Przez analogię z arbitralnym prostopadłościennym prostokątem, kiedy trzeba było pomnożyć wszystkie jego wymiary liniowe. Wzór zostanie zapisany w następujący sposób (# 6):
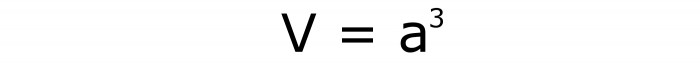
Metoda 2: znana jest cała powierzchnia
W takim przypadku będziesz musiał podzielić znaną wartość przez 6. Od odpowiedzi pośredniej wyodrębnij pierwiastek kwadratowy i podnieś liczbę do sześcianu. Jeśli piszemy tę formułę, otrzymamy następujące (# 7):
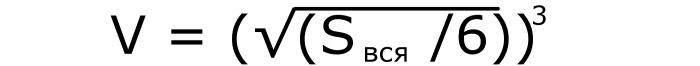
Metoda 3: ze względu na przekątną ścianę sześcianu
Aby dowiedzieć się, jak obliczyć objętość sześcianu, w tym przypadku należy wykonać następujące kroki. Najpierw zbuduj znaną wartość w sześcianie, a następnie pomnóż ją przez pierwiastek kwadratowy z 2 i podziel przez 4. Wzór tego problemu (nr 8):
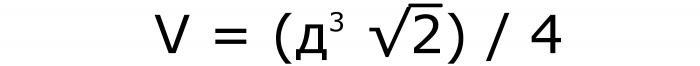
To równanie uzyskuje się w ten sposób: znaną przekątną należy podzielić przez pierwiastek z dwóch. Następnie zbuduj liczbę do trzeciego stopnia. Po wykonaniu przekształceń sześcian przekątnej uzyskuje się w liczniku, a 2√2 w mianowniku. Matematyka wymaga, aby nie było żadnej irracjonalnej liczby poniżej linii. Dlatego się go pozbywają pomnażając przez √2. Następnie w liczniku pojawia się √2, a w mianowniku 4.
Metoda 4: Przekrój sześcianu
Formuła, która powie ci, jak znaleźć objętość sześcianu, będzie zawierała akcje: wyrównanie przekątnej, pomnożenie jej przez pierwiastek równy 3 i podzielenie przez tylko 9. Zostanie to zapisane w ten sposób (nr 9):
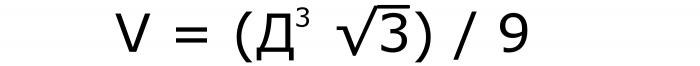
Podobnie jak w poprzedniej formule, w tym rekordzie przekątna jest najpierw podzielona na pierwiastek z trzech i podniesiona do sześcianu. Po przemianach w mianowniku pojawia się także irracjonalność, z której należy odejść. Tak więc wartość √3 pojawia się w liczniku, a pod linią - 9.
Przykłady zadań
Zadanie pierwsze. Podano sześcian o boku 12 cm, obliczyć jego objętość i wyrazić odpowiedź w metrach kwadratowych.
W tym zadaniu trudniej będzie przetłumaczyć odpowiedź na inne jednostki, niż zdecydować, jak znaleźć objętość sześcianu. Aby ukończyć pierwszą część zadania, będziesz potrzebował formuły zapisanej pod numerem 6. Po wstawieniu cyfry 12 do sześcianu odpowiedź będzie wynosić 1728 cm 3 . Teraz musimy pamiętać, jak je przetłumaczyć na metry sześcienne. W tym celu odpowiedź należy podzielić na 100 razy trzykrotnie. Sto pochodziło z faktu, że było sto centymetrów na metr. Podział jest wykonywany trzykrotnie, ponieważ jednostki w zadaniu są sześcienne. Zatem 1728 podzielone przez 100 da 17,28. Po drugim podziale będzie to 0,1728. Trzecie działanie da odpowiedź 0,001728 m 3 . To jest odpowiedź na problem: objętość kostki wynosi 0,001728 m 3 .
Zadanie drugie. Istnieje sześcian o powierzchni całej powierzchni równej 600 dm 2 . Znajdź objętość kształtu i wyraż ją w metrach sześciennych.
Aby odpowiedzieć na pytanie o to zadanie, potrzebna będzie formuła numer 7. Pierwsza operacja jest znaną liczbą podzieloną przez 6. Odpowiedź daje 100. Łatwo jest wyodrębnić pierwiastek kwadratowy z niego, będzie to 10. Teraz musisz zbudować pierwszą dziesiątkę w sześcianie. Okazuje się, że pożądana wartość jest równa 1000 dm 3 . Pozostaje przekonwertować go na m 3 . Podobnie jak w poprzednim zadaniu, podział zostanie wykonany trzykrotnie, tylko dzielnik będzie miał 10. Bo jest dziesięć decymetrów na metr. Po podziale odpowiedź wynosi 1 m 3 . Odpowiedź: objętość wynosi 1 m 3 .
Trzecie zadanie. Mając sześcian o przekątnej długości powierzchni równej √2 mm. Musisz obliczyć objętość.
Ósma formuła pomoże znaleźć odpowiedź na ten problem. Pierwszą rzeczą, którą musisz zbudować sześcian o znanej wartości. Pierwiastek kwadratowy z 2 na trzecim stopniu daje wartość 2√2. Po pomnożeniu przez √2 otrzymujemy liczbę 4. Ostatnia akcja polega na podzieleniu jej przez 4. Odpowiedź: objętość sześcianu wynosi 1 mm 3 .
Czwarte zadanie. Wiadomo, że przekątna sześcianu wynosi 3 m. Wymagane jest obliczenie jego objętości.
Łatwo będzie znaleźć odpowiedź na ten problem, używając wzoru numer 9. Wartość podana w warunku musi zostać podniesiona do sześcianu. Okazuje się 27. Po podzieleniu przez 9, odpowiedź będzie 3. A ostatnia akcja powinna zostać pomnożona przez pierwiastek kwadratowy z 3. Odpowiedź problemu będzie 3 3 m 3 .