Nieprawidłowe ułamki: jak nauczyć się rozwiązywać z nimi przykłady?

Kiedy słowo "frakcje" uruchamia się wiele gęsiej skórki. Ponieważ pamiętam szkołę i zadania, które zadecydowały o matematyce. To była odpowiedzialność, która musiała zostać spełniona. A jeśli traktować zadania zawierające poprawne i niepoprawne ułamki jako puzzle? W końcu wielu dorosłych rozwiązuje krzyżówki cyfrowe i japońskie. Zrozum zasady i wszystko. Tak jest tutaj. Trzeba tylko uchwycić teorię - i wszystko się ułoży. A przykłady staną się sposobem na wytrenowanie mózgu.

Jakie rodzaje frakcji istnieją?

Na początek, co to jest. Ułamek to liczba, która ma ułamek jednego. Może być napisany w dwóch formach. Pierwszy nazywa się zwykłym. Oznacza to, że ma poziomą lub ukośną. Jest równy znakowi podziału.

W takim zapisie liczba nad myślnikiem nazywana jest licznikiem, a poniżej mianem.

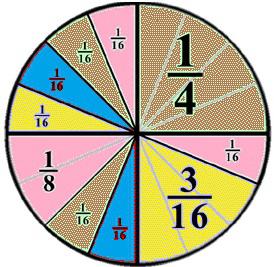
Wśród zwykłych przydziela prawidłowe i nieregularne ułamki. W pierwszym przypadku licznik według modułu jest zawsze mniejszy od mianownika. Dlatego nazywają się źle, ponieważ mają wszystko przeciwne. Wartość właściwej frakcji jest zawsze mniejsza niż jeden. Podczas gdy błąd jest zawsze większy niż ten numer.

Są jeszcze liczby mieszane, to znaczy te, które mają części całkowite i ułamkowe.

Drugi rodzaj rekordu jest dziesiętny. O niej osobna rozmowa.

Jaka jest różnica pomiędzy nieregularnymi ułamkami i liczbami mieszanymi?

W gruncie rzeczy nic. To tylko inny rekord tej samej liczby. Nieprawidłowe ułamki po prostych działaniach łatwo stają się liczbami mieszanymi. I odwrotnie.

Wszystko zależy od konkretnej sytuacji. Czasami w zadaniach wygodniej jest użyć niewłaściwej frakcji. Czasami konieczne jest przetłumaczenie go na liczbę mieszaną, a następnie przykład zostanie rozwiązany bardzo łatwo. Dlatego to, czego należy używać: nieprawidłowe ułamki, liczby mieszane - zależy od obserwacji rozwiązywania problemów.

Liczba mieszana jest również porównywana z sumą części całkowitej i ułamkowej. A drugi to zawsze mniej niż jeden.

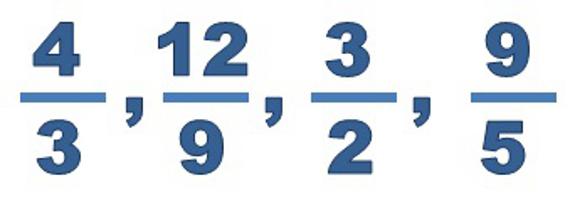
Jak przedstawić liczbę mieszaną w postaci niewłaściwej frakcji?

Jeśli chcesz wykonać czynność z kilkoma liczbami zapisanymi w różnych formach, musisz zrobić to samo. Jedną z metod jest reprezentowanie liczb jako nieregularnych frakcji.

W tym celu należy wykonać akcje zgodnie z tym algorytmem:

• pomnóż mianownik przez część całkowitą;
• dodaj do wyniku wartość licznika;
• napisz odpowiedź powyżej linii;
• mianownik pozostawia to samo.

Oto przykłady, jak pisać niepoprawne ułamki liczb mieszanych:

• 17 ¼ = (17 x 4 + 1): 4 = 69/4;
• 39 ½ = (39 x 2 + 1): 2 = 79/2.

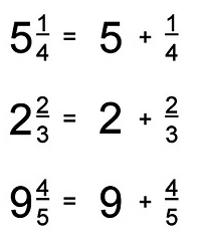
Jak napisać niewłaściwą frakcję w postaci liczby mieszanej?

Poniższa technika jest przeciwieństwem powyższego. To znaczy, gdy wszystkie liczby mieszane są zastępowane nieregularnymi ułamkami. Algorytm działań będzie następujący:

• podziel licznik przez mianownik, aż do uzyskania równowagi;
• wpisz iloraz na miejscu całej części wymieszanej;
• pozostała część powinna znajdować się powyżej linii;
• dzielnik będzie mianownikiem.

Przykłady takiej transformacji:

76/14; 76:14 = 5 z pozostałą ilością 6; odpowiedź to 5 liczb całkowitych i 6/14; część ułamkowa w tym przykładzie musi zostać zmniejszona o 2, będzie to 3/7; ostateczna odpowiedź to 5 3/7.

108/54; po podziale część 2 otrzymuje się bez reszty; Oznacza to, że nie wszystkie nieregularne frakcje mogą być reprezentowane jako liczba mieszana; odpowiedź to liczba całkowita - 2.

Jak przekształcić liczbę całkowitą w nieregularną część?

Są sytuacje, w których takie działanie jest konieczne. Aby uzyskać błędne ułamki z wcześniej znanym mianem, musisz uruchomić ten algorytm:

• pomnóż liczbę całkowitą przez pożądany mianownik;
• zapisz tę wartość powyżej linii;
• umieść pod nim mianownik.

Najprostsza opcja, gdy mianownik jest jeden. Wtedy nic nie musi być pomnożone. Wystarczy napisać liczbę całkowitą podaną w przykładzie i umieścić jednostkę poniżej linii.

Przykład : 5, aby utworzyć nieregularną część z mianownikiem 3. Po pomnożeniu 5 przez 3, otrzymujemy 15. Ta liczba będzie mianownikiem. Odpowiedz na frakcję pracy: 15/3.

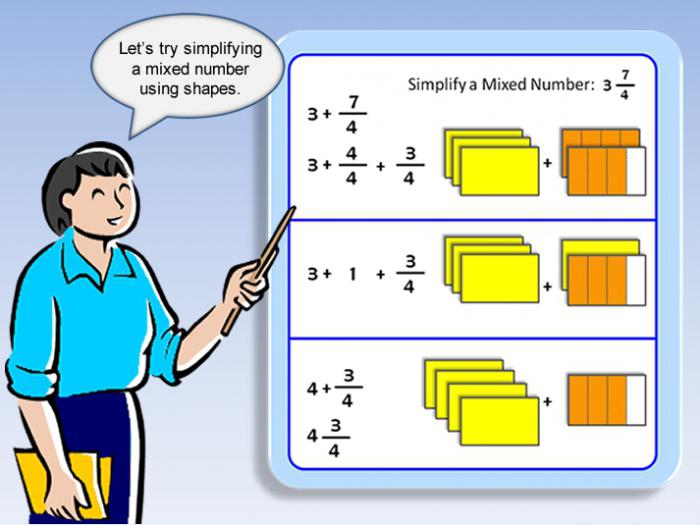
Dwa podejścia do rozwiązywania zadań o różnych liczbach

W tym przykładzie należy obliczyć sumę i różnicę, a także iloczyn i iloraz dwóch liczb: 2 liczby całkowite 3/5 i 14/11.

W pierwszym podejściu liczba mieszana będzie reprezentowana jako niewłaściwa część.

Po wykonaniu opisanych wyżej kroków otrzymasz następującą wartość: 13/5.

Aby dowiedzieć się, jaka jest kwota, musisz przenieść ułamek do tego samego mianownika. 13/5 po pomnożeniu przez 11 stanie się 143/55. Liczba 14/11 po pomnożeniu przez 5 będzie miała postać: 70/55. Aby obliczyć kwotę, wystarczy dodać liczniki: 143 i 70, a następnie zapisać odpowiedź z jednym mianownikiem. 213/55 - ta niepoprawna część jest odpowiedzią na problem.

Po znalezieniu różnicy odejmuje się te same liczby: 143 - 70 = 73. Odpowiedź będzie ułamkiem: 73/55.

Kiedy mnożenie 13/5 i 14/11 nie musi prowadzić do wspólnego mianownika. Wystarczy pomnożyć w parach liczniki i mianowniki. Odpowiedź będzie: 182/55.

To samo z dzieleniem. Aby uzyskać prawidłowe rozwiązanie, musisz zamienić podział na mnożenie i obrócić dzielnik: 13/5: 14/11 = 13/5 x 11/14 = 143/70.

W drugim podejściu ułamek nieregularny zamienia się w liczbę mieszaną.

Po wykonaniu akcji algorytm 14/11 zamieni się w liczbę mieszaną z częścią całkowitą 1 i ułamkową 3/11.

Podczas obliczania kwoty należy osobno dodać całe i ułamkowe części. 2 + 1 = 3, 3/5 + 3/11 = 33/55 + 15/55 = 48/55. Ostateczna odpowiedź to 3 punkt 48/55. W pierwszym podejściu była frakcja 213/55. Możesz sprawdzić poprawność, tłumacząc ją na liczbę mieszaną. Po podzieleniu 213 na 55 otrzymujemy iloraz 3, a pozostały 48. Łatwo zauważyć, że odpowiedź jest prawidłowa.

Podczas odejmowania znak "+" zamienia się na "-". 2 - 1 = 1, 33/55 - 15/55 = 18/55. Aby sprawdzić odpowiedź z poprzedniego podejścia, musisz przetłumaczyć na mieszaną liczbę: 73 jest podzielne przez 55, a otrzymujemy iloraz 1, a reszta 18.

Mieszanie liczb jest niewygodne dla znalezienia pracy i ilorazu. Zawsze zaleca się, aby przejść do niewłaściwych ułamków.