Logarytmy: reguły, podstawowe właściwości i formuły

Logarytmy i zasady działania z nimi są dość pojemne i proste. Dlatego zrozumienie tego tematu nie będzie trudne. Po opanowaniu wszystkich zasad logarytmów naturalnych każdy problem zostanie rozwiązany niezależnie. Pierwsza znajomość tego tematu może wydawać się nudna i bezsensowna, ale dzięki logarytmom udało się rozwiązać wiele problemów XVI-wiecznych matematyków. "O co chodzi?" - myślałeś. Przeczytaj artykuł do końca i przekonaj się, że ten rozdział "Czarina nauk" może zainteresować nie tylko matematyków, naukowców zajmujących się naukami ścisłymi, ale także zwykłych uczniów szkół średnich.

Definicja logarytmu

Zacznijmy od definicji logarytmu. Jak mówi wiele podręczników: logarytm liczby b na podstawie a (log _a b) to pewna liczba c, dla której obowiązuje ta równość: b = a ^c . Innymi słowy, logarytm jest pewnym stopniem, w jakim budujemy bazę, aby uzyskać określoną liczbę. Należy jednak pamiętać, że logarytm logu formularza b ma sens tylko wtedy, gdy: a> 0; a jest liczbą inną niż 1; b> 0, dlatego wyciągamy wniosek, że logarytm można znaleźć tylko dla liczb dodatnich.

Klasyfikacja logarytmów według bazy

Logarytmy mogą być dowolną liczbą dodatnią u podstawy. Ale są też dwa typy: logarytmy naturalne i dziesiętne.

• Logarytm naturalny - logarytm o podstawie e (e jest liczbą Eulera, numerycznie w przybliżeniu równą 2,7, liczba nieracjonalna, która została wprowadzona dla funkcji wykładniczej y = e ^x ) jest oznaczana jako ln a = log _e a;
• Logarytm dziesiętny jest logarytmem o podstawie 10, czyli log ₁₀ a = lg a.

Podstawowe zasady logarytmów

Najpierw musisz zapoznać się z podstawową tożsamością logarytmiczną: ^{log _a b} = b, a następnie przestrzegać dwóch podstawowych zasad:

• log _a 1 = 0 - ponieważ dowolna liczba w stopniu zero to 1;
• zaloguj _a = 1.

Dzięki odkryciu logarytmu nie jest nam trudno rozwiązać absolutnie jakiekolwiek równanie wykładnicze, którego odpowiedź nie może być wyrażona w liczbach naturalnych, a jedynie irracjonalna. Na przykład: 5 ^x = 9, x = log ₅ 9 (ponieważ nie ma naturalnych x dla tego równania).

Akcje z logarytmami

• log _a (x · y) = log _a x + log _a y - aby znaleźć logarytm produktu, musisz dodać logarytmy czynników. Zauważ, że podstawy logarytmów są takie same. Jeśli piszemy to w odwrotnej kolejności, otrzymamy regułę dodawania logarytmów.
• log _a xy = log _a x - log _a y - aby znaleźć logarytm konkretu, musisz znaleźć różnicę między logarytmami dywidendy a dzielnikiem. Uwaga: logarytmy mają tę samą podstawę. Pisząc w odwrotnej kolejności otrzymujemy regułę odejmowania logarytmów.

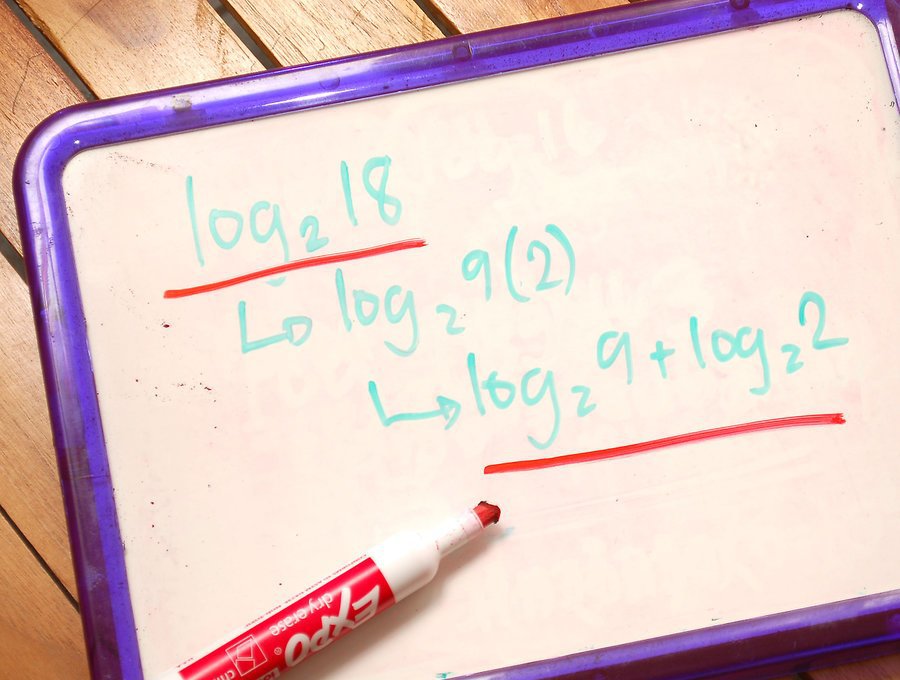
• log a kx p = (p / k) * log a x - tak więc jeśli w argumencie znajdują się stopnie i podstawa logarytmu, to można je usunąć ze znaku logarytmicznego.
• log a x = log a c x c jest szczególnym przypadkiem poprzedniej reguły, kiedy wykładniki są równe, mogą być zmniejszone.
• log a x = (log b x) (log b a) to tak zwany moduł przejściowy, procedura przekształcania logarytmu w inną bazę.
• log a x = 1 / log x a jest szczególnym przypadkiem przejścia, zmiany miejsc bazy i danej liczby. Całe wyrażenie, w przenośni, odwraca się, a logarytm z nową bazą pojawia się w mianowniku.

Historia logarytmów

W XVI wieku konieczne stało się przeprowadzenie wielu obliczeń przybliżających do rozwiązywania praktycznych problemów, głównie w astronomii (na przykład określanie położenia statku przez Słońce lub gwiazdy).

Potrzeba ta rosła szybko, a znaczna trudność powodowała mnożenie i dzielenie liczb wielocyfrowych. A matematyczny matematyk Napier zdecydował zastąpić pracochłonne mnożenie zwykłym dodatkiem do obliczeń trygonometrycznych, porównując niektóre postępy w tym kierunku. Następnie podział został zastąpiony przez prostszą i bardziej niezawodną procedurę - odejmowanie, a w celu wyodrębnienia rdzenia n-tego stopnia konieczne jest podzielenie logarytmu radicand przez n. Rozwiązanie tak trudnego zadania w matematyce wyraźnie odzwierciedlało cele Napera w nauce. Oto jak o tym pisał na początku swojej książki Rabdologiya:

Zawsze próbowałem, na ile pozwalały mi moje zdolności i zdolności, uwolnić ludzi od trudności i nudy obliczeń, których kłopotliwość zwykle odstrasza bardzo wiele osób od studiowania matematyki.

Logarytm nazwy został zaproponowany przez samego Napiera, uzyskano go przez połączenie słów greckich, co w połączeniu oznaczało "liczbę relacji".

Podstawę logarytmu wprowadził Spadel. Pożyczył Eulera od teorii stopni i przeszedł do teorii logarytmów. Koncepcja logarytmizmu stała się sławna dzięki Koppowi w XIX wieku. Wykorzystanie logarytmów naturalnych i dziesiętnych, a także ich oznaczeń, ukazało się dzięki Cauchy'emu.

W 1614 r. John Napier opublikował po łacinie esej "Opis niesamowitej tabeli logarytmów". Przedstawiono krótki opis logarytmów, reguł i ich właściwości. Tak więc termin "logarytm" został ustanowiony w naukach ścisłych.

Operacja logarytmiczna i pierwsza wzmianka o niej pojawiły się dzięki Wallisowi i Johannowi Bernoulli, a została ona ostatecznie ustalona przez Eulera w XVIII wieku.

Jest to zasługa Eulera w rozszerzaniu logarytmicznej funkcji postaci y = log _a x do domeny złożonej. W pierwszej połowie XVIII wieku ukazała się jego książka "Wprowadzenie do analizy nieskończoności", w której znalazły się współczesne definicje funkcji wykładniczych i logarytmicznych.

Funkcja logarytmiczna

(имеет смысл, только если: а > 0, а ≠ 1). Funkcja postaci y = log _a x (ma sens tylko wtedy, gdy: a> 0 i ≠ 1).

• Funkcja logarytmiczna jest określona przez zbiór wszystkich liczb dodatnich, ponieważ dziennik rekordów x istnieje tylko pod warunkiem - x> 0;
• Ta funkcja może przyjmować absolutnie wszystkie wartości z zestawu R (liczby rzeczywiste). Ponieważ każda liczba rzeczywista b ma wartość dodatnią x, aby spełnić log równości _a x = b, to znaczy, to równanie ma pierwiastek - x = a ^b (wynika to z faktu, że log _a a ^b = b).
• Funkcja zwiększa się w przedziale a> 0 i zmniejsza się w przedziale 0 <a <1.
• Jeśli a> 0, to funkcja przyjmuje wartości dodatnie dla x> 1.

Należy pamiętać, że wszelkie wykresy funkcji logarytmicznej y = log _i x mają jeden punkt stacjonarny (1; 0), ponieważ log _i 1 = 0. Jest to wyraźnie widoczne na ilustracji poniższego wykresu.

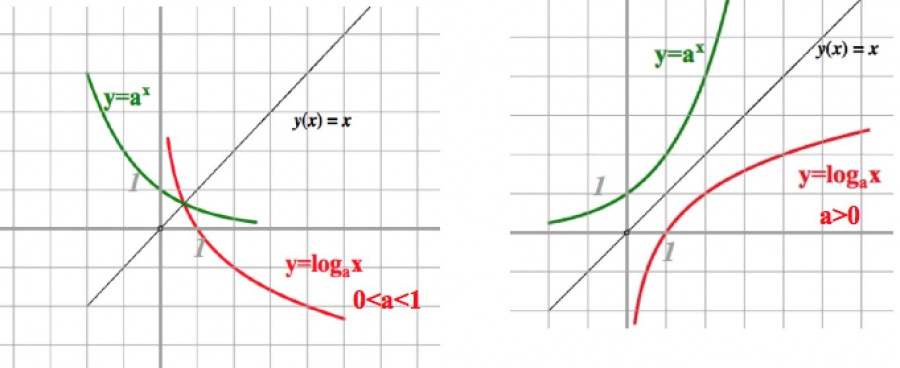
Jak widzimy na zdjęciach, funkcja nie ma równości ani dziwności, nie ma największych ani najmniejszych wartości, nie jest ograniczona z góry ani z dołu.

Funkcja logarytmiczna y = log _a x i funkcja wykładnicza y = a ^x , gdzie (a> 0 i ≠ 1) są wzajemnie odwrotne. Można to zobaczyć na obrazie ich wykresów.

Rozwiązywanie problemów z logarytmami

Zwykle rozwiązanie problemu zawierającego logarytmy polega na konwersji ich do standardowej postaci lub ma na celu uproszczenie wyrażeń pod znakiem logarytmu. Lub konieczne jest przełożenie zwykłych liczb naturalnych na logarytmy z niezbędną podstawą, w celu przeprowadzenia dalszych operacji w celu uproszczenia ekspresji.

Istnieją pewne subtelności, o których nie należy zapominać:

• Przy rozwiązywaniu nierówności, gdy obie części stoją pod logarytmami zgodnie z regułą z jedną bazą, nie spiesz się, aby "odrzucić" znak logarytmiczny. Zapamiętaj przestrzenie monotoniczne funkcji logarytmicznej. Ponieważ jeśli podstawa jest większa niż 1 (przypadek, gdy funkcja się zwiększa) - znak nierówności pozostaje niezmieniony, ale gdy podstawa jest większa niż 0 i mniejsza niż 1 (przypadek, gdy funkcja maleje) - znak nierówności zmienia się na przeciwny;
• _а х = b, а>0, а≠1 и х>0, чтобы не потерять корней из-за неучтенной области допустимых значений. Nie zapominaj o definicji logarytmu: log _i x = b, a> 0 i ≠ 1 i x> 0, aby nie stracić korzeni z powodu niezapisanego zakresu prawidłowych wartości. TLD (dopuszczalny zakres wartości) istnieje dla prawie wszystkich złożonych funkcji.

Podczas rozwiązywania równań logarytmicznych zaleca się stosowanie transformacji równoważnych. Musisz też być ostrożny i brać pod uwagę możliwe przekształcenia, które mogą prowadzić do utraty niektórych korzeni.

Są to powszechne, ale na dużą skalę błędy, które napotykali wielu w poszukiwaniu właściwej odpowiedzi dla zadania. Nie ma tak wielu reguł rozwiązywania logarytmów, więc ten temat jest prostszy niż inne i kolejne, ale powinien być dobrze zrozumiany.

Wniosek

Temat ten na pierwszy rzut oka może wydawać się skomplikowany i kłopotliwy, ale eksplorując go coraz głębiej, zaczynasz rozumieć, że temat się kończy, a trudności nie spowodowały niczego. Sprawdziliśmy wszystkie właściwości, reguły, a nawet błędy związane z tematem logarytmów. Sukcesy w nauce!