Modelowanie - co to jest? Metoda symulacji. Modelowanie matematyczne i komputerowe

Aby zrozumieć istotę matematycznego modelowania, należy wziąć pod uwagę podstawowe definicje, cechy procesu.

Esencja tego terminu

Modelowanie to proces tworzenia i stosowania modelu. Jest uważany za dowolny abstrakcyjny lub materialny obiekt, zastępujący w procesie badania rzeczywistego obiektu modelowania. Ważną kwestią jest zachowanie właściwości niezbędnych do pełnej analizy tematu.

Symulacja komputerowa jest wersją poznania, opartą na modelu matematycznym. Zakłada on system nierówności, równań i znaków logicznych, które w pełni odzwierciedlają wszystkie cechy zjawiska lub przedmiotu.

Modelowanie matematyczne obejmuje określone obliczenia, wykorzystanie technologii komputerowej. Aby wyjaśnić ten proces, potrzebne są dodatkowe badania. Modelowanie komputerowe z powodzeniem radzi sobie z tym zadaniem.

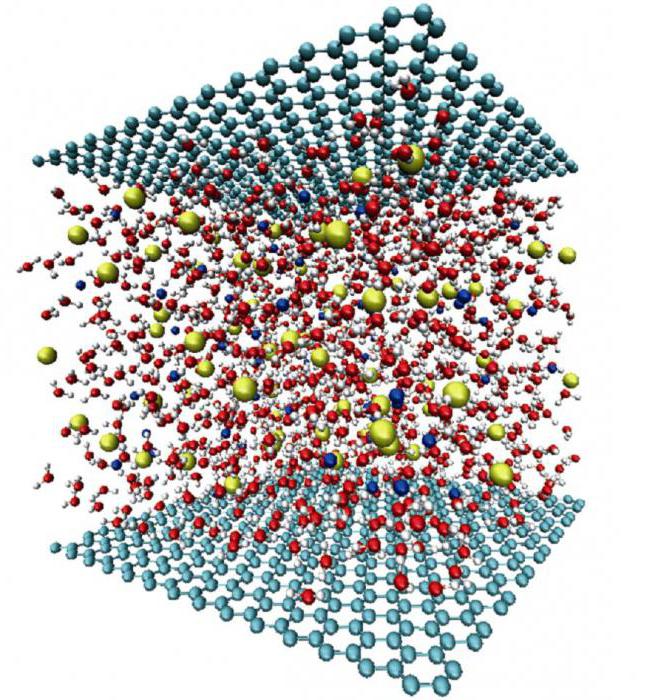
Specyfika symulacji komputerowej

Ta metoda badania złożonych systemów jest uważana za skuteczną i wydajną. Bardziej wygodne i łatwiejsze jest analizowanie modeli komputerowych, ponieważ można wykonywać różne operacje obliczeniowe. Jest to szczególnie prawdziwe w przypadkach, gdy z przyczyn fizycznych lub materialnych prawdziwe eksperymenty nie pozwalają uzyskać pożądanego rezultatu. Konsystencja takich modeli pozwala określić główne czynniki determinujące parametry badanego oryginału.

Takie zastosowanie matematycznego modelowania umożliwia identyfikację zachowania obiektu w różnych warunkach, w celu ujawnienia wpływu różnych czynników na jego zachowanie.

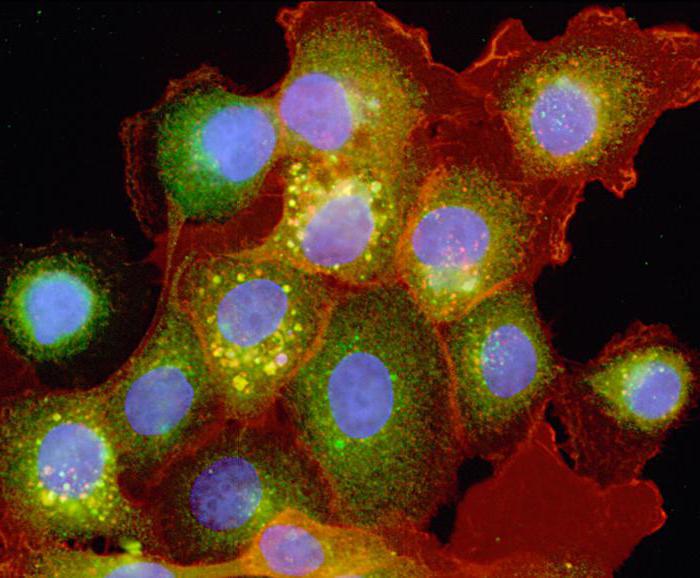
Podstawy symulacji komputerowej

Na czym opiera się takie modelowanie? Co to są badania oparte na ICT? Na początek każda symulacja komputerowa opiera się na pewnych zasadach:

• modelowanie matematyczne w celu opisania badanego procesu;
• zastosowanie innowacyjnych modeli matematycznych do szczegółowego rozpatrywania analizowanych procesów.

Różnorodność modelowania

Obecnie istnieją różne metody modelowania matematycznego: imitacyjne i analityczne.

Wariant analityczny jest związany z badaniem abstrakcyjnych modeli obiektu rzeczywistego w postaci równań różniczkowych, algebraicznych, które zapewniają czystą technologię komputerową, która może dać dokładne rozwiązanie.

Modelowanie symulacyjne polega na badaniu modelu matematycznego w postaci określonego algorytmu odtwarzającego funkcjonowanie analizowanego systemu za pomocą sekwencyjnego wykonywania systemu prostych obliczeń i operacji.

Funkcje budowania modelu komputerowego

Rozważmy bardziej szczegółowo, jak takie modelowanie występuje. Jakie są etapy badań komputerowych? Na początek proces opiera się na odejściu od analizowanego obiektu lub zjawiska.

Takie modelowanie składa się z dwóch głównych etapów: stworzenia modelu jakościowego i ilościowego. Studium komputerowe polega na przeprowadzeniu systemu obliczeń na komputerze osobistym, którego celem jest analiza, systematyzowanie, porównywanie wyników badania z faktycznym zachowaniem analizowanego obiektu. Jeśli to konieczne, dodatkowe udoskonalenie modelu.

Etapy modelowania

Jaka jest symulacja? Jakie są etapy badań komputerowych? Wybierz więc następujący algorytm działań dotyczących budowy modelu komputerowego:

Etap 1 Określanie celów i zadań pracy, identyfikacja przedmiotu modelowania. Ma gromadzić dane, stawiać pytania, identyfikować cele i formy badań, opisywać uzyskane wyniki.

Etap 2 Analiza i badanie systemu. Wykonywany jest opis obiektu, tworzenie modelu informacyjnego, dobór oprogramowania i sprzętu, wybrane są przykłady modelowania matematycznego.

Etap 3 Przejście do modelu matematycznego, opracowanie metody projektowania, wybór algorytmu działania.

4 etap. Wybór języka programowania lub medium do modelowania, omówienie opcji analizy, zapis algorytmu w określonym języku programowania.

Etap 5 Polega ona na przeprowadzeniu złożonych eksperymentów obliczeniowych, obliczeniach debugowania i przetwarzaniu uzyskanych wyników. Jeśli to konieczne, na tym etapie, dostosowanie symulacji.

6 etap. Interpretacja wyników.

W jaki sposób analizowana jest symulacja? Co to jest oprogramowanie badawcze? Przede wszystkim oznacza to wykorzystanie tekstowych, graficznych edytorów, arkuszy kalkulacyjnych, pakietów matematycznych, które pozwalają uzyskać maksymalny wynik z badań.

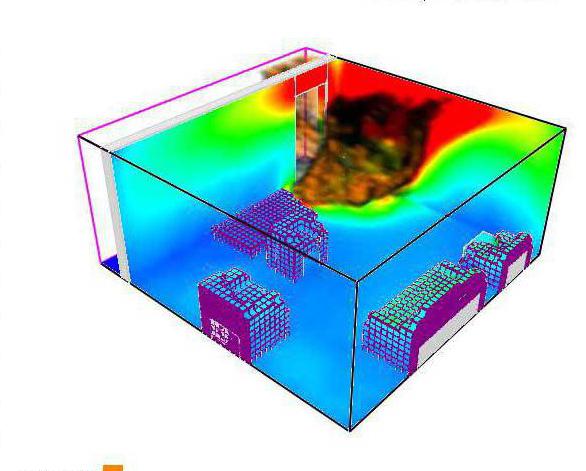
Przeprowadzenie eksperymentu obliczeniowego

Wszystkie metody modelowania matematycznego oparte są na eksperymentach. Pod nimi są powszechnie rozumiane eksperymenty prowadzone z modelem lub obiektem. Polegają one na realizacji określonych działań, pozwalających określić zachowanie próbki eksperymentalnej w odpowiedzi na proponowane działania.

Nie można wyobrazić sobie eksperymentu obliczeniowego bez wykonywania obliczeń związanych z użyciem sformalizowanego modelu.

Podstawy modelowania matematycznego obejmują badania z rzeczywistym obiektem, ale operacje obliczeniowe wykonywane są z dokładną kopią (modelem). Wybierając określony zestaw początkowych wskaźników modelu, po zakończeniu działań obliczeniowych możliwe jest uzyskanie optymalnych warunków dla pełnego funkcjonowania obiektu rzeczywistego.

Na przykład, mając matematyczne równanie opisujące przepływ analizowanego procesu, kiedy zmieniają się współczynniki, warunki początkowe i pośrednie, możemy przyjąć zachowanie obiektu. Ponadto można w pewnych warunkach przewidzieć wiarygodne przewidywanie zachowania tego obiektu lub zjawiska naturalnego. W przypadku nowego zestawu danych źródłowych ważne jest przeprowadzenie nowych eksperymentów obliczeniowych.

Porównanie danych

Aby przeprowadzić odpowiednią weryfikację obiektu rzeczywistego lub stworzonego modelu matematycznego, a także ocenić wyniki badań nad technologią komputerową z wynikami eksperymentu przeprowadzonego na próbce doświadczalnej na pełną skalę, przeprowadza się porównanie wyników badań.

Z tego, co rozbieżność między informacjami uzyskanymi w trakcie badań, zależy od decyzji o zbudowaniu gotowej próbki lub dostosowania modelu matematycznego.

Taki eksperyment pozwala zastąpić kosztowne, naturalne badania z wykorzystaniem obliczeń w technologii komputerowej, w najkrótszym możliwym czasie, aby przeanalizować możliwości wykorzystania obiektu, określić warunki jego rzeczywistego działania.

Modelowanie w środowiskach

Na przykład środowisko programistyczne wykorzystuje trzy etapy modelowania matematycznego. Na etapie tworzenia algorytmu i modelu informacyjnego wyznaczają wartości, które będą parametrami wejściowymi, wynikami badań i ich typem.

W razie potrzeby utwórz specjalne algorytmy matematyczne w formie schematów blokowych zapisanych w określonym języku programowania.

Następnie przeprowadza się sam eksperyment obliczeniowy, do którego program jest ładowany do pamięci operacyjnej urządzenia komputerowego, a następnie rozpoczyna się proces obliczeniowy.

Eksperyment komputerowy polega na analizie wyników uzyskanych w obliczeniach, ich dostosowaniu. Wśród ważnych etapów takiego badania odnotowujemy testowanie algorytmu, analizę wydajności roboczej programu.

Jego debugowanie obejmuje wyszukiwanie i eliminowanie błędów, które prowadzą do niepożądanego wyniku, pojawienia się błędów w obliczeniach.

Testowanie obejmuje sprawdzenie poprawności działania programu, a także ocenę niezawodności jego poszczególnych komponentów. Proces polega na sprawdzeniu działania programu, jego przydatności do badania określonego zjawiska lub obiektu.

Arkusze kalkulacyjne

Modelowanie za pomocą arkuszy kalkulacyjnych umożliwia pokrycie dużej liczby zadań w różnych obszarach tematycznych. Są uważane za uniwersalne narzędzie, które pozwala rozwiązać czasochłonne zadanie obliczania parametrów ilościowych obiektu.

W przypadku tej wersji symulacji następuje transformacja algorytmu rozwiązania problemu, nie ma potrzeby rozwijania interfejsu obliczeniowego. W tym przypadku istnieje etap debugowania, który obejmuje usuwanie błędów danych, wyszukiwanie połączeń między komórkami, identyfikację formuł obliczeniowych.

W miarę postępu prac pojawiają się dodatkowe zadania, np. Wyprowadzanie wyników na nośniki papierowe, racjonalna prezentacja informacji na monitorze komputera.

Kolejność działań

Modelowanie odbywa się w arkuszu kalkulacyjnym dla określonego algorytmu. Najpierw określa się cele badawcze, identyfikuje się podstawowe parametry i relacje, a na podstawie otrzymanych informacji opracowuje się określony model matematyczny.

Dla jakościowego rozważenia modelu wykorzystuje się cechy początkowe, pośrednie, a także końcowe, uzupełniając je rysunkami, diagramami. Za pomocą wykresów i wykresów uzyskać wizualną reprezentację wyników pracy.

Modelowanie w środowisku DBMS

Pozwala to rozwiązać następujące zadania:

• przechowuj informacje, przeprowadzaj ich terminową edycję;
• organizować dostępne dane na konkretnych podstawach;
• stworzyć różne kryteria wyboru danych;
• przedstawić dostępne informacje w dogodny sposób.

Ponieważ model jest opracowywany na podstawie danych źródłowych, tworzone są optymalne warunki opisu cech obiektu za pomocą specjalnych tabel.

W tym samym czasie informacje są sortowane, dane są wyszukiwane i filtrowane, algorytmy są tworzone do wykonywania obliczeń. Za pomocą panelu informacyjnego komputera można tworzyć różne formularze ekranowe, a także opcje uzyskiwania wydrukowanych raportów papierowych na temat postępu eksperymentu.

Jeżeli uzyskane wyniki nie pokrywają się z planowanymi opcjami, zmieniają parametry, przeprowadzają dodatkowe badania.

Zastosowanie modelu komputerowego

Eksperyment obliczeniowy i symulacja komputerowa są nowe metody naukowe badania. Pozwalają one na uaktualnienie urządzenia komputerowego używanego do budowy modelu matematycznego, aby określić, udoskonalić, skomplikować eksperymenty.

Wśród najbardziej obiecujących zastosowań praktycznych, pełnoprawny eksperyment obliczeniowy, reaktory projektowe dla potężnych elektrowni jądrowych. Ponadto obejmuje to tworzenie magnetohydrodynamicznych przetworników energii elektrycznej, a także zrównoważony długoterminowy plan dla kraju, regionu, przemysłu.

Za pomocą komputerowego i matematycznego modelowania możemy zaprojektować urządzenia niezbędne do badania reakcji termojądrowych i procesów chemicznych.

Symulacja komputerowa i eksperymenty obliczeniowe umożliwiają zredukowanie odległych "nie-matematycznych" obiektów do kompilacji i rozwiązania problemu matematycznego.

Otwiera to ogromne możliwości zastosowania aparatu matematycznego w systemie z nowoczesną techniką komputerową do rozwiązywania problemów związanych z opanowaniem przestrzeni kosmicznej, "podbojem" procesów atomowych.

To właśnie modelowanie stało się jednym z najważniejszych wariantów wiedzy o różnych procesach otaczających i zjawiskach przyrodniczych. Wiedza ta jest złożonym i czasochłonnym procesem, obejmującym wykorzystanie systemu różnych typów modelowania, począwszy od opracowania zredukowanych modeli obiektów rzeczywistych, kończąc wybór specjalnych algorytmów dla złożonych obliczeń matematycznych.

W zależności od tego, jakie procesy lub zjawiska będą analizowane, wybrane algorytmy działania, wzory matematyczne do obliczeń. Symulacja komputerowa pozwala uzyskać pożądany wynik, ważne informacje o właściwościach i parametrach obiektu lub zjawiska przy minimalnych kosztach.