Moment bezwładności: wzór. Moment bezwładności ciała

Aby zmienić szybkość ruchu ciała w przestrzeni, konieczne jest podjęcie pewnego wysiłku. Fakt ten dotyczy wszystkich rodzajów ruchu mechanicznego i jest związany z obecnością bezwładności właściwości obiektów mających masę. W tym artykule omówiono rotację ciał i przedstawiono koncepcję momentu bezwładności.

Czym jest rotacja w zakresie fizyki?

Odpowiedź na to pytanie może dać każdemu, ponieważ ten fizyczny proces nie różni się od jego koncepcji w życiu codziennym. Proces rotacji jest ruchem obiektu o skończonej masie wzdłuż okrągłej ścieżki wokół jakiejś urojonej osi. Można podać następujące przykłady rotacji:

• Ruch kół samochodu lub roweru.
• Obrót łopat helikoptera lub wentylatora.
• Ruch naszej planety wokół osi i wokół Słońca.

Jakie wielkości fizyczne charakteryzują proces rotacji?

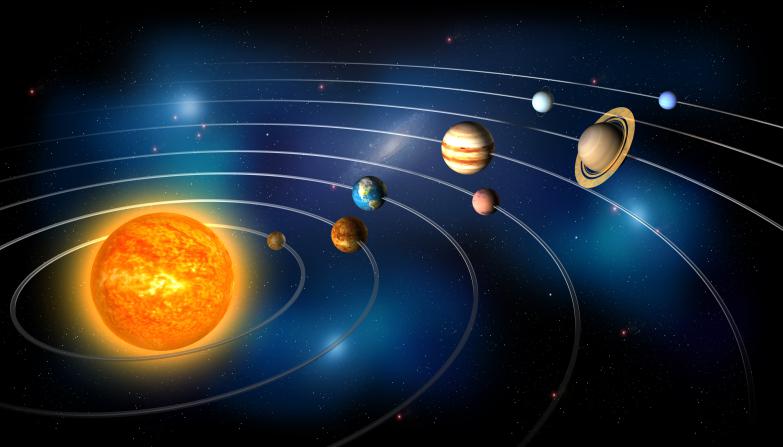
Ruch kołowy opisany jest przez zbiór wielkości w fizyce, z których główne są wymienione poniżej:

• r jest odległością do osi materialnego punktu masy m.
• ω i α to odpowiednio prędkość kątowa i przyspieszenie. Pierwsza wartość pokazuje, ile radianów (stopni) ciało obraca się wokół osi w ciągu jednej sekundy, druga wartość opisuje szybkość zmian w czasie pierwszego radiana.
• L jest momentem pędu, który jest podobny do podobnej charakterystyki w ruchu liniowym.
• I - moment bezwładności ciała. Ta wartość jest omówiona szczegółowo poniżej.
• M to moment siły. Charakteryzuje stopień zmiany wartości L, jeśli zastosowana jest siła zewnętrzna.

Ilości te są powiązane ze sobą za pomocą następujących formuł ruchu obrotowego:

1. L = I * ω

2. M = I * α

Pierwsza formuła opisuje ruch kołowy ciała w przypadku braku działania zewnętrznych momentów sił. W powyższej formie odzwierciedla prawo zachowania momentu pędu L. Drugie wyrażenie opisuje przypadek przyspieszenia lub spowolnienia obrotu ciała w wyniku działania momentu siły M. Oba wyrażenia są często używane przy rozwiązywaniu problemów dynamiki wzdłuż trajektorii kołowej.

Jak widać z tych wzorów, moment bezwładności wokół osi (I) w nich jest stosowany jako pewien współczynnik. Przyjrzyjmy się tej wartości bardziej szczegółowo.

Skąd pochodzi wartość I?

W tej sekcji rozważamy najprostszy przykład obrotu: ruch kołowy materialnego punktu masy m, którego odległość od osi obrotu wynosi r. Ta sytuacja jest pokazana na rysunku.

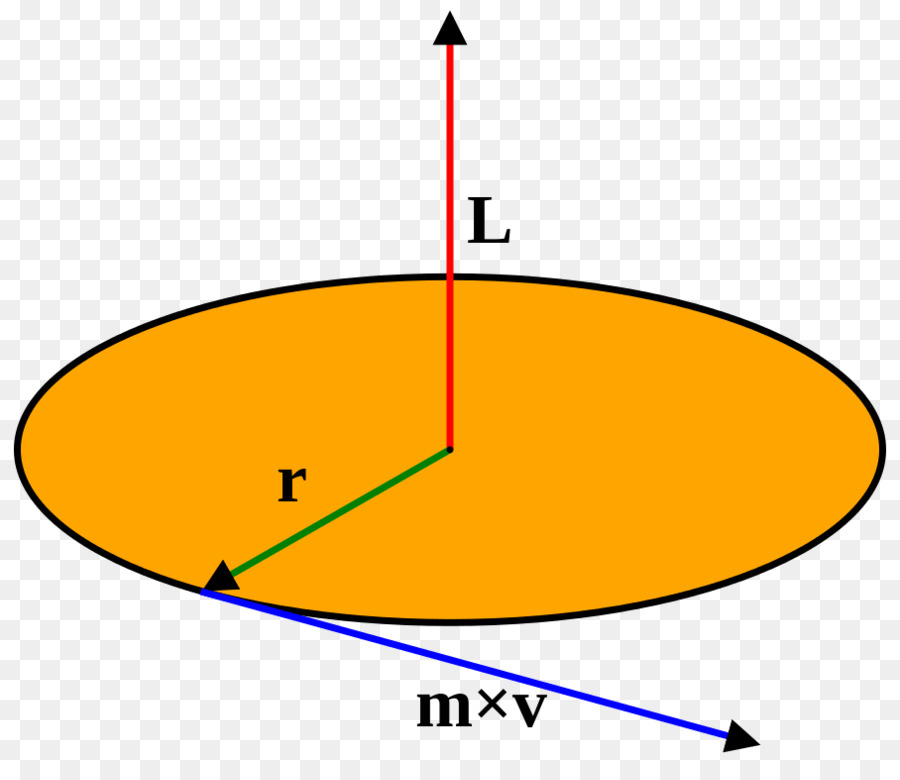
Zgodnie z definicją, moment pędu L jest zapisywany jako iloczyn ramienia r przez impuls liniowy p punktów:

L = r * p = r * m * v, ponieważ p = m * v

Biorąc pod uwagę, że prędkość liniowa i kątowa są ze sobą powiązane poprzez odległość r, tę równość można przepisać jako:

v = ω * r => L = m * r ² * ω

Iloczyn masy punktu materialnego przez kwadrat odległości do osi obrotu nazywany jest momentem bezwładności. Powyższy wzór zostanie przepisany w tym przypadku w następujący sposób:

I = m * r ² => L = I * ω

Oznacza to, że otrzymaliśmy wyrażenie, które zostało podane w poprzednim akapicie, i wprowadziliśmy wartość I.

Ogólna formuła dla wielkości ciała I

Wyrażenie dla momentu bezwładności o masie m punktu materialnego jest podstawowe, to znaczy pozwala obliczyć tę wartość dla dowolnego ciała mającego dowolny kształt i nierównomierny rozkład masy w nim. Aby to zrobić, konieczne jest podzielenie rozpatrywanego obiektu na małe elementy o masie m _i (liczba całkowita i jest liczbą elementu), a następnie pomnożenie każdego z nich przez kwadrat odległości r _i ² do osi, wokół której rozważa się obrót, i dodanie wyników. Opisaną metodę znajdowania wartości I można zapisać matematycznie w następujący sposób:

I = Σ _i (m _i * r _i ² )

Jeśli ciało jest podzielone w taki sposób, że i-> ∞, wówczas dana suma zostaje zastąpiona całką masy ciała m:

I = ∫ _m (r _i ² * dm)

Ta całka jest równoważna innej całce względem objętości ciała V, ponieważ dV = ρ * dm:

I = ρ * ∫ _V (r _i ² * dV)

Wszystkie trzy formuły są używane do obliczenia momentu bezwładności ciała. W tym przypadku, w przypadku dyskretnego rozkładu masy w układzie, korzystne jest użycie pierwszego wyrażenia. Przy ciągłym rozkładzie masy zastosuj trzecie wyrażenie.

Własności I i jego znaczenie fizyczne

Opisana procedura uzyskiwania ogólnego wyrażenia dla I pozwala wyciągnąć pewne wnioski na temat właściwości tej fizycznej ilości:

• jest addytywny, tzn. całkowity moment bezwładności układu można przedstawić jako sumę momentów jego poszczególnych części;
• zależy to od rozkładu masy w układzie, a także od odległości do osi obrotu, im większa jest ta druga, tym większa I;
• nie zależy od sił M działających w układzie momentów i prędkości obrotowej ω.

Fizyczne znaczenie I polega na tym, jak mocno system zapobiega jakiejkolwiek zmianie jego prędkości obrotowej, to znaczy moment bezwładności charakteryzuje stopień "gładkości" uzyskanych przyspieszeń. Na przykład koło rowerowe można łatwo obracać do dużych prędkości kątowych, a także łatwo je zatrzymać, ale aby zmienić obrót koła zamachowego na wale korbowym samochodu, będzie to wymagało znacznego wysiłku i pewnego czasu. W pierwszym przypadku istnieje system z małym momentem bezwładności, w drugim - z dużym.

Wartość I niektórych ciał dla osi obrotu przechodzącej przez środek masy

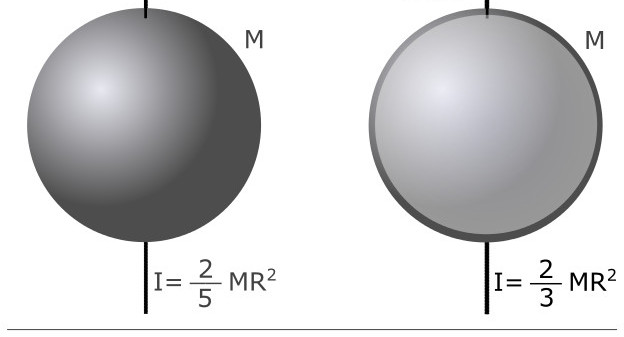
Jeśli zastosujemy integrację nad objętością dla dowolnych ciał o arbitralnym rozkładzie mas, możemy uzyskać wielkość I. W przypadku obiektów jednorodnych, które mają idealny kształt geometryczny, problem ten został już rozwiązany. Wzory dla momentu bezwładności dla pręta, tarczy i kulki o masie m, w których ich składowa jest równomiernie rozłożona, podano poniżej:

• Rdzeń. Oś obrotu biegnie do niej prostopadle. I = m * L 2/12, gdzie L to długość pręta.
• Dysk o dowolnej grubości. Moment bezwładności z osią obrotu przechodzącą prostopadle do jej płaszczyzny poprzez środek masy oblicza się w następujący sposób: I = m * R 2/2, gdzie R jest promieniem dysku.
• Piłka. Ze względu na wysoką symetrię tej figury, dla dowolnego położenia osi przechodzącej przez jej środek, I = 2/5 * m * R2, tutaj R jest promieniem kuli.

Poniżej podajemy dwa przykłady rozwiązywania problemów związanych z zastosowaniem ogólnego wzoru do obliczania I i używania właściwości addytywności tej ilości.

Zadanie obliczania wartości I dla układu z dyskretnym rozkładem masy

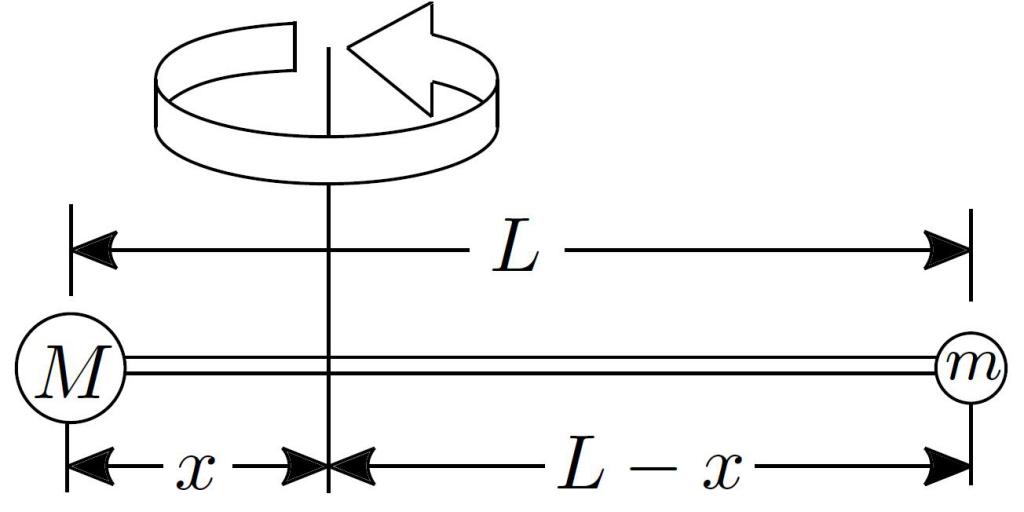
Wyobraź sobie pręt o długości 0,5 metra, wykonany z twardego i lekkiego materiału. Ten pręt jest zamocowany na osi w taki sposób, że biegnie prostopadle do niej dokładnie pośrodku. Na drążku zawieszone są trzy obciążniki w następujący sposób: po jednej stronie osi znajdują się dwa obciążniki o masie 2 kg i 3 kg, położone odpowiednio w odległości 10 cm i 20 cm od jej końca; z drugiej strony pojedynczy pręt o wadze 1,5 kg jest zawieszony na końcu pręta. W przypadku tego układu konieczne jest obliczenie momentu bezwładności I i określenie, przy jakiej prędkości ω pręt się obróci, jeśli siła 50 N zostanie przyłożona do jednego z jego końców na 10 sekund.

Ponieważ można pominąć masę pręta, należy obliczyć moment I dla każdego obciążenia i dodać uzyskane wyniki, aby uzyskać pełny moment systemu. W zależności od stanu zadania, od osi ciężar 2 kg wynosi 0,15 m (0,25-0,1), obciążenie 3 kg wynosi 0,05 m (0,25-0,20), obciążenie 1,5 kg 0,25 m. Wykorzystując wzór na moment I punktu materialnego otrzymujemy:

I = I ₁ + I ₂ + I ₃ = m ₁ * r ₁ ² + m ₂ * r ₂ ² + m ₃ * r ₃ ² = 2 * (0,15) ² + 3 * (0,05) ² + 1,5 * (0,25) ² = 0,14 625 kg * m ² .

Należy zauważyć, że podczas wykonywania obliczeń wszystkie jednostki miary zostały przeniesione do układu SI.

Aby określić prędkość kątową obrotu pręta po działaniu siły, należy zastosować wzór z momentem siły, który został podany w drugim akapicie artykułu:

M = I * α

Ponieważ α = Δω / Δt i M = r * F, gdzie r jest długością ramion, otrzymujemy:

r * F = I * Δω / Δt => Δω = r * F * Δt / I

Biorąc pod uwagę, że r = 0,25 m, zastępujemy liczby w formule, otrzymujemy:

Δω = r * F * Δt / I = 0,25 * 50 * 10 / 0,14625 = 854,7 rad / s

Wynikowa wartość jest dość duża. Aby uzyskać normalną prędkość, należy podzielić Δω na 2 * pi radianów:

f = Δω / (2 * pi) = 854,7 / (2 * 3,1416) = 136 s- ¹

Tak więc przyłożona siła F do końca pręta z ciężarkami w ciągu 10 sekund spowoduje jego obrót do częstotliwości 136 obrotów na sekundę.

Obliczenie wartości I dla pręta, gdy oś przechodzi przez jej koniec

Niech będzie jednorodny pręt o masie m i długości L. Niezbędne jest określenie momentu bezwładności, jeżeli oś obrotu znajduje się na końcu prostopadłej do niego pręta.

Używamy ogólnego wyrażenia dla I:

I = ρ * ∫ _V (r _i ² * dV)

Rozbijając rozpatrywany przedmiot na objętości elementarne, zauważamy, że dV można zapisać jako dr * S, gdzie S jest przekrojem poprzecznym pręta, a dr jest grubością elementu łupiącego. Zamieniając to wyrażenie na formułę, mamy:

I = ρ * S * ∫ _L (r ² * dr)

Ta całka jest dość prosta do obliczenia, otrzymujemy:

I = ρ * S * (r 3/3) | ₀ ^L => I = ρ * S * L 3/3

Ponieważ objętość pręta to S * L, a masa to ρ * S * L, otrzymujemy ostateczną formułę:

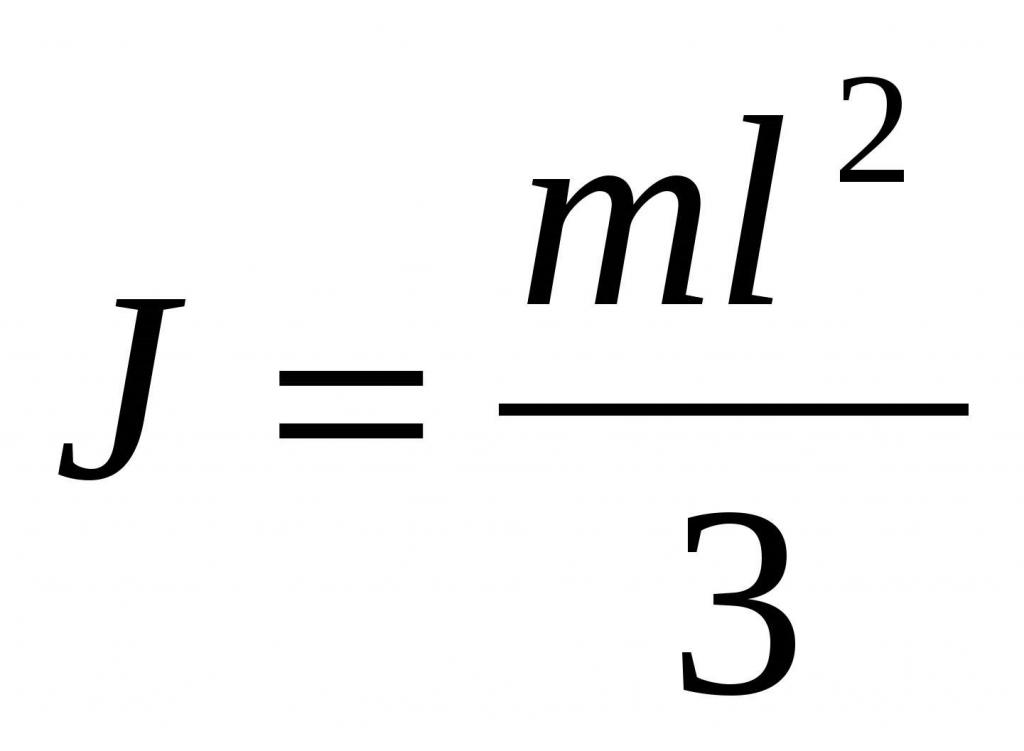
Warto zauważyć, że moment bezwładności dla tego samego pręta, gdy oś przechodzi przez środek masy, jest 4 razy mniejszy niż uzyskana wartość (m * L 2/3 / (m * L 2/12) = 4).