Systemy liczbowe: przykłady. Tłumaczenie systemów liczbowych

Mówiąc w najprostszym języku, system liczbowy jest sposobem na reprezentowanie liczb. Kiedyś przy obliczaniu stosowano metodę obliczeniową 10. Na przykład inne systemy liczbowe mają podstawę 16 (szesnastkowy), 8 (ósemkowy) i 2 (binarny).

Prehistoryczne czasy

Podobnie jak pierwsze próby pisania pojawiły się po opracowaniu mowy, pierwsze próby graficznego przedstawienia liczb pojawiły się po tym, jak ludzie nauczyli się liczyć. Prawdopodobnie najwcześniejszym sposobem policzenia jest jakiś system do liczenia obiektów fizycznych, takich jak kamyczki czy kijki. Sądząc po zwyczajach obecnych ludów tubylczych, a także najstarszych śladach znalezisk pisanych lub rzeźbiarskich, najwcześniejsze postacie to były proste cięcia na deskach, zadrapania na kamieniu, ślady na kawałku ceramiki itp. Bez stałych jednostek, bez monet, bez handlu oprócz najbardziej prymitywnego handlu, systemu podatkowego i innych potrzeb niż te, które wspierały życie, ludzie nie potrzebowali numerów pisanych aż do początku tak zwanych czasów historycznych.

Pierwsze metody liczenia

Kiedy stało się konieczne, aby często liczyć liczby przekraczające 10, numeracja powinna być usystematyzowana i uproszczona; zazwyczaj robiono to przy użyciu grupy lub grupy. W rzeczywistości najwcześniejsze zarejestrowane liczby były prostymi liniowymi znakami dla małych liczb ze specjalną formą dla 10. Te symbole pojawiły się w Egipcie już w roku 3400 pne oraz w Mezopotamii już w 3000 roku pne, na Krecie (około 1200 p.n.e. AD) oraz w Indiach (około 300 pne).

Oczywiście szczególne miejsce zajmuje liczba 10 liczby ludzkich palców, co potwierdza nowoczesne wykorzystanie tej podstawy nie tylko w strukturze logicznej systemu dziesiętnego, ale także w nazwach liczb w wielu językach.

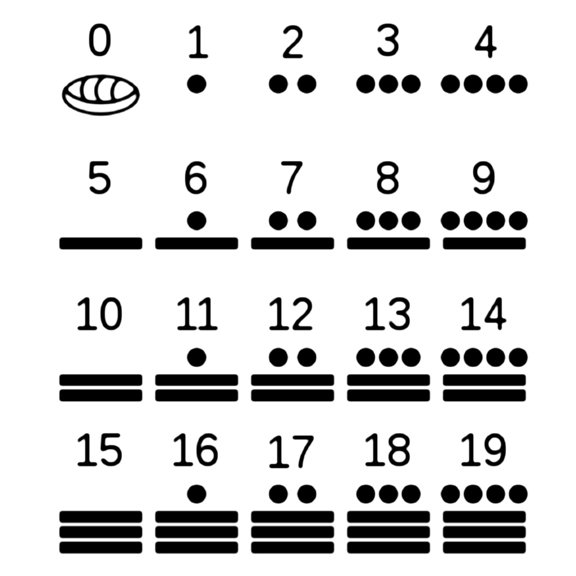
Różnorodność metod liczenia

Nie należy jednak wnioskować, że 10 jest albo jedyną możliwą podstawą, albo jedyną faktycznie stosowaną. Istnieje wiele przykładów systemów liczbowych. Binarny, w którym liczenie jest "jeden, dwa, dwa i jeden, dwa i dwa, dwa i dwa i jeden", itp., Znajduje się wśród najstarszych plemion Australii, w wielu językach narodów Cieśniny Torres i sąsiedniego wybrzeża Nowej Gwinei, wśród niektórych afrykańskich pigmejów i różnych południowoamerykańskich plemion. Tubylcze ludy Ziemi Ognistej i kontynent Ameryki Południowej używają systemów liczbowych z trzema i czterema bazami. System podstawowy numer pięć jest bardzo stary, ale w czystej postaci wydaje się być stosowany obecnie tylko w niektórych plemionach Ameryki Południowej. W innych miejscach jest ono połączone z dziesiętnym lub dwunastym systemem dziesiętnym, gdzie podstawa wynosi 20. Podobnie, system oparty na 6 jest rzadkością w północno-zachodniej Afryce i związany jest z 12-cio podstawowym systemem dwunastnicy.

W toku rozwoju historycznego system dziesiętny ostatecznie przyćmił wszystkie inne. Niemniej jednak wciąż istnieje wiele innych systemów, które są wykorzystywane głównie w przemyśle komercyjnym i mieszkaniowym. Tak więc podstawa 12 występuje jako liczba cali w stopach, miesiące w roku, uncje w funtach i dwa razy na 12 godzin dziennie, a także kilkanaście używanych w obliczeniach. Podstawa 60 znajduje się podczas pomiaru czasu i kątów.

Systemy cyfrowe

Pierwsze cyfry pierwotne to |, ||, ||| itp., na przykład w Egipcie i starożytnej Grecji, lub -, = ,, itp., jak w Azji Wschodniej. Ta metoda obliczeniowa odpowiadała prostym potrzebom ludzi. W miarę jak życie stawało się coraz bardziej złożone, zapotrzebowanie na liczbę grup liczb stało się oczywiste, a był to zaledwie mały krok od prostego systemu z nazwami tylko jednego i dziesiątego na pojawienie się innych liczb specjalnych, na podstawie których można określić, ile systemów liczbowych istniało i istnieje. Czasami proces ten był niesystematyczny. Na przykład Jukagir Syberii rozważał "jeden, dwa, trzy, trzy i jeden, pięć, dwa trzy, dwa trzy i jeden, dwa cztery, dziesięć z jednym brakującym, dziesięć". Zwykle jednak system bardziej regularny doprowadził do tego, że większość tych systemów można sklasyfikować, przynajmniej w kategoriach ogólnych, zgodnie z zasadami logicznymi, które się za nimi kryją.

Proste systemy grupujące

Na podstawie jego wartości system liczbowy można uznać za metodę grupowania liczb. W czystej formie prosty system grupowania to przypisanie specjalnych nazw małym liczbom, podstawa b i jej mocom b2, b3 itd. Do stopnia bk wystarczającego do reprezentowania wszystkich liczb, które są rzeczywiście niezbędne do użycia. Numery pośrednie są następnie tworzone przez dodawanie, każdy znak powtarza się wymaganą liczbę razy, tak jak napisano 23 - XXIII - cyframi rzymskimi.

Najwcześniejszym przykładem tego typu systemu liczb jest wzór znaleziony w egipskich hieroglifach. Był używany przez starożytnych Egipcjan do pisania na kamieniu.

Pozycyjne systemy numerów

Należą do nich te, w których pozycja (cyfra) podczas pisania liczby określa jej wartość. System liczb dziesiętnych jest przykładem systemu pozycyjnego, w którym, po przyjęciu zasady b, specjalne nazwy są przypisane do liczb 1, 2, ..., b-1, a wszystkie większe liczby są zapisywane jako sekwencje tych liczb. Jest to jedyny spośród różnych systemów liczbowych, które można wykorzystać do opisu dużych liczb. Dzieje się tak, ponieważ każdy z pozostałych typów nadaje specjalne nazwy różnym liczbom wyższym niż b, a wszystkie liczby wymagają nieskończonej liczby nazw. Sukces systemu liczb pozycyjnych zależy od tego, że dla dowolnej podstawy b każda liczba N może być napisana jednoznacznie w formie:

N = anbn + an - 1bn - 1 + ⋯ + a1b + a0,

gdzie a, an - 1, ..., a0 są liczbami; to znaczy liczby z grupy 0, 1, ..., b - 1. Następnie N w bazie b może być reprezentowane przez ciąg znaków anan - 1 ... a1a0. Zasada ta została zastosowana w multiplikatywnych systemach grupujących. System pozycyjny wywodzi się z multiplikatywności, po prostu wykluczając nazwy stopni b, b2 itd., I jest określany w zależności od pozycji liczb dla przedstawienia tych informacji. Jednak konieczne jest użycie pewnego znaku dla zera, aby wskazać brakujące uprawnienia podstawowe; w przeciwnym razie 792 może oznaczać, na przykład, 7M9X2 (to jest 7 092) lub 7C9X2 (792).

Rozwój w różnych krajach

Przykładem tego rodzaju systemu liczb jest metoda opracowana przez Babilończyków (około 3000-2000 lat pne). W tym przypadku podstawą była liczba 60. Taki system nazywa się szesnastkowo. Przy tak dużej podstawie niewygodne byłoby posiadanie niepowiązanych nazw dla liczb 0, 1, ..., 59, więc dla tych liczb użyto prostego systemu grupowania do dolnego 10.

Oprócz faktu, że system ten był uciążliwy ze względu na dużą bazę, system babiloński cierpiał bardzo późno z powodu braku znaku zerowego.

Podczas wczesnych wypraw na Jukatant odkryto kolejny przykład systemu liczb Maya. Był używany głównie w kalendarzu, a nie do obliczeń komercyjnych lub innych. Był to dobrze rozwinięty system pozycyjny. Jego podstawą była liczba 20. Liczby 0, 1, ..., 19, jak w Babilonie, są tworzone przez prosty system grupowania, w tym przypadku do podstawy 5.

Ani systemy Majów, ani babilońskie nie są idealne do obliczeń arytmetycznych, ponieważ liczby poniżej 20 lub 60 nie były reprezentowane przez pojedyncze znaki.

Ewolucja

Dalszy rozwój tej idei związany jest z Indianami, którzy jako pierwsi wykorzystali zero we współczesnym obrazie. W systemach pozycjonowania potrzebna jest pewna postać, aby oznaczyć miejsce, w którym baza nie została znaleziona. Hindusi oznaczono to kropką lub małym okręgiem, któremu nadano nazwę sunya, sanskryckie słowo "puste". Następnie około 800 AD ta nazwa została przekazana Arabom, a w tłumaczeniu wartość nie uległa zmianie. Następnie został wprowadzony do języka łacińskiego (około 1200), podczas gdy wymowa została zachowana, ale wartość została zignorowana. Kolejne zmiany doprowadziły do ​​nowoczesnego wyznaczenia.

System hindusko-arabski

Istnieje kilka różnych opinii na temat pochodzenia współczesnych liczb zachodnich: zazwyczaj mówią one o ich arabskim pochodzeniu, ale lepiej jest rozważyć hindusko-arabski. W tym przypadku twierdzi się, że ich pochodzenie jest związane z Arabami, Persami, Egipcjanami i Hindusami. Nie jest wykluczone, że komunikacja między kupcami służyła jako możliwość przeniesienia tych symboli z kraju do kraju, tak aby współczesne postacie zachodnie mogły pochodzić z różnych źródeł. Jednak, o ile wiadomo, krajem, który pierwszy użył największej liczby tych liczbowych form, są Indie. 1, 4 i 6 znajdują się w inskrypcjach Ashoki (III wpne); 2, 4, 6, 7 i 9 pojawiają się w inskrypcjach Nana Ghat po około stuleciu; i 2, 3, 4, 5, 6, 7 i 9 w jaskiniach Nasika pierwszego lub drugiego wieku naszej ery. Wszystkie te liczby miały formę w dużej mierze podobną do dzisiejszej.

Zalety, jakie posiada doskonały system pozycjonowania, są tak liczne i tak oczywiste, że cyfry hindusko-arabskie i podstawa 10 były akceptowane niemal wszędzie. Można powiedzieć, że jest to najbliższe podejście do uniwersalnego ludzkiego języka.

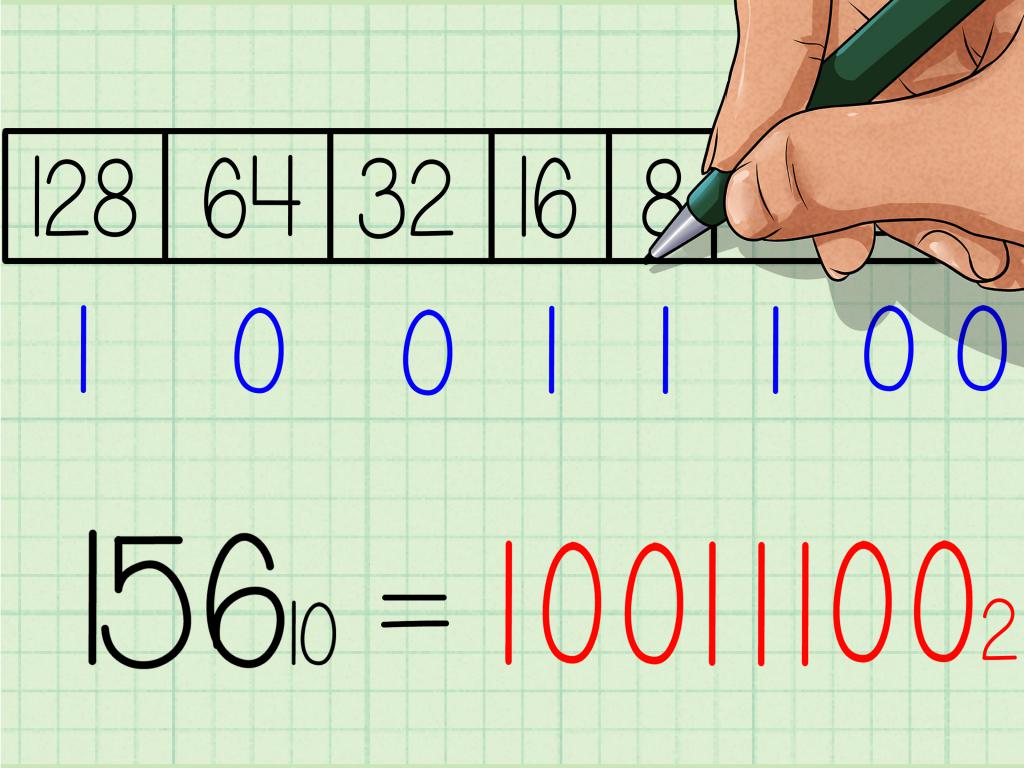
System binarny

Istnieje jednak obszar, w którym zwykły system dziesiętny nie jest najlepszy: komputer. Tutaj binarny system pozycyjny ma więcej zalet niż dziesiętny. W tym systemie, podstawa 2 określa, ile liczb znajduje się w systemie liczb binarnych: tutaj są tylko dwie cyfry - 0 i 1; numer dwa jest tutaj przedstawiony jako 10, ponieważ odgrywa on taką samą rolę jak dziesięć w systemie dziesiętnym.

Liczba binarna jest zwykle znacznie dłuższa niż odpowiadająca jej liczba dziesiętna; na przykład 256 058 ma binarną reprezentację 111 11010 00001 11010. Cyfra binarna, podobnie jak jednostka w systemie liczbowym, przenosi mniej informacji niż cyfra dziesiętna. Powodem większej długości liczby binarnej jest to, że cyfra binarna rozróżnia tylko dwie możliwości: 0 lub 1, natomiast cyfra dziesiętna rozróżnia 10 możliwości.

Systemy liczb ósemkowych i szesnastkowych

Ich użycie jest również związane z komputerami i programowaniem.

Starszym komputerowym systemem numeracji jest liczba ósemkowa, gdzie podstawą jest liczba 8. Liczby używane w tym systemie to: 0, 1, 2, 3, 4, 5, 6 i 7. Wartość "osiem" jest zapisywana jako "1 oś i 0 jednostek". lub 10. Każda wartość pozycji jest ośmiokrotnie różna od następnej.

Z technicznego punktu widzenia istnieje tak wiele różnych protokołów języka komputerowego dla systemu ósemkowego.

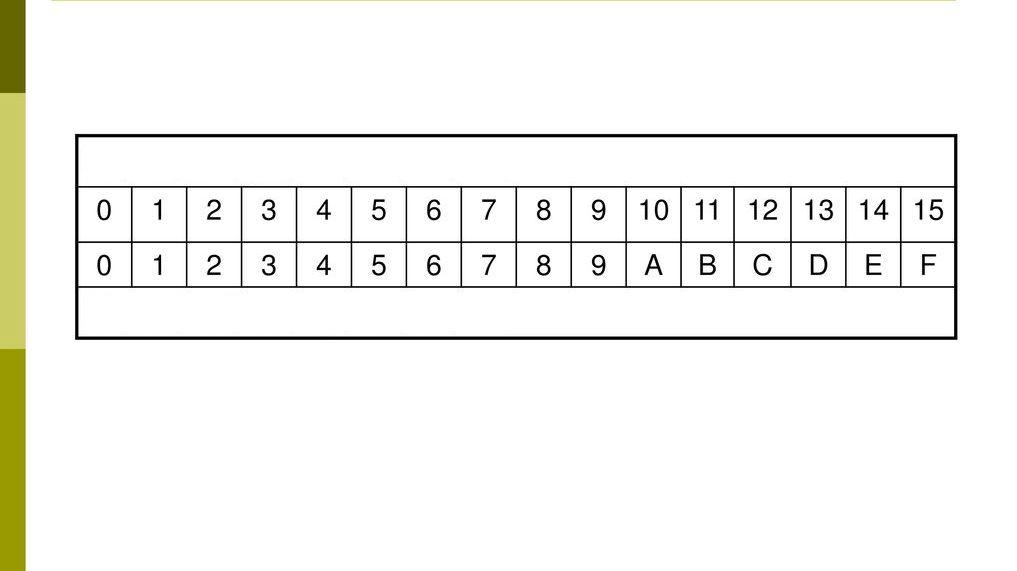
Drugi system nazywa się heksadecymalnie, ponieważ ten system ma podstawę równą 16. Prawidłowe szyfry obejmują normalne znaki dziesiętne 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9, a także sześć znaków alfabetu A, B, C , D, E i F, w sumie szesnaście. Wartość każdej pozycji różni się od poprzedniej szesnastokrotnie.

Systemy ósemkowe i szesnastkowe nie miałyby znaczenia, gdyby nie ich łatwość konwersji do systemu binarnego. Ich głównym celem jest służenie jako "skrócona" metoda oznaczania liczby reprezentowanej elektronicznie w postaci binarnej. Ponieważ podstawy ósemkowego (8) i szesnastkowego (16) systemu są parzyste i wielokrotne binarnej podstawy (2), bity binarne mogą być zgrupowane razem, a liczby w systemach liczbowych mogą być bezpośrednio przekształcone na cyfry ósemkowe lub szesnastkowe. Podczas konwersji na system ósemkowy bity binarne są pogrupowane na trzy (ponieważ 23 = 8), a w systemie szesnastkowym bity binarne są zgrupowane na cztery (ponieważ 24 = 16).

Podobnie, konwersja liczb w liczbach ósemkowych lub szesnastkowych do liczb binarnych jest wykonywana przy użyciu każdej cyfry ósemkowej lub szesnastkowej i przekształcania jej w równoważną binarną (3 lub 4-bitową) grupę, a następnie wszystkie grupy bitów są łączone.