Wysokość piramidy: definicja, formuły, obliczenia

Jedną z wielkości objętościowych badanych w toku geometrii przestrzennej jest piramida. Ważną cechą tej figury jest jej wysokość. W artykule podamy definicję wysokości piramidy i podamy wzory, przez które jest połączona z innymi cechami liniowymi.

Czym jest piramida

Pod piramidą rozumiem geometryczny kształt przestrzenny, który uzyskuje się poprzez połączenie wszystkich narożników wielokąta z jednym punktem w przestrzeni. Poniższy rysunek pokazuje rozmieszczenie linii (krawędzi) dla ostrosłupów czworokątnych i pięciokątnych.

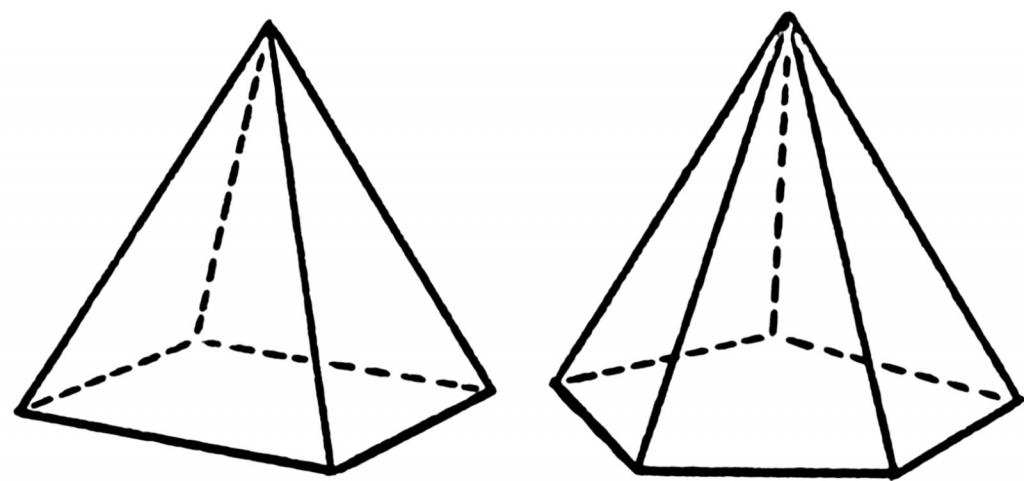
Poligonalna twarz kształtu nazywana jest jego podstawą. Punkt, w którym łączą się trójkątne powierzchnie, nazywa się wierzchołkiem. Aby wyznaczyć wysokość piramidy, zaznaczone elementy są ważne.

Wysokość ciała

Wysokość piramidy nazywana jest prostopadłą, która od góry jest obniżana do płaszczyzny podstawy. Ważne jest, aby zrozumieć, że z każdego wierzchołka należącego do podstawy figury można również narysować prostopadle do odpowiedniej trójkątnej ściany, ale nie będzie ona widoczna jako wysoka. Wysokość piramidy jest jedyną prostopadłą, która jest jedną z jej ważnych cech liniowych.

Każdy uczeń wie, że każda postać płaska ma geometryczne centrum (w fizyce odpowiada centrum masy). Na przykład geometryczny środek dla dowolnego trójkąta jest wyznaczany przez punkt przecięcia jego środkowej części, dla równoległoboku, punktu przecięcia przekątnych. Jeśli wysokość piramidy przecina jej podstawę w geometrycznym środku, wówczas figurę nazywa się linią prostą. Piramida jest prosta, ma wielobok bazowy o tych samych bokach i kątach, nazywany prawidłową.

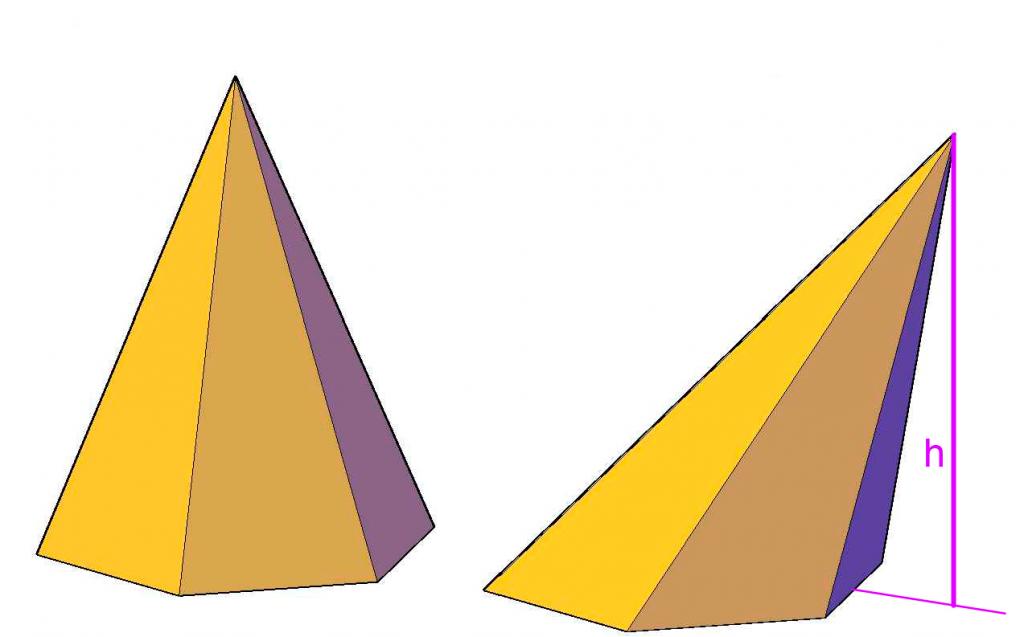
Powyższy rysunek pokazuje różnicę pomiędzy niewłaściwą piramidą a właściwą. Można zauważyć, że wysokość nieregularnego kształtu leży poza jego podstawą, podczas gdy w regularnej piramidzie sześciokątnej wysokość znajduje się wewnątrz kształtu, przecinając jego podstawę w geometrycznym środku.

Ważne właściwości wszystkich zwykłych piramid są następujące:

• wszystkie powierzchnie boczne są trójkątami równoramiennymi i są sobie równe;
• długości bocznych żeber i apotemy są takie same.

Wzory na wysokość zwykłej piramidy

Istnieją cztery podstawowe charakterystyki liniowe dla każdej piramidy:

• strona podstawy;
• krawędź boczna;
• apotema strony bocznej;
• wysokość figury.

Wszystkie są matematycznie powiązane ze sobą. Oznacz długość boku podstawy przez a, wysokość - h, apotemp - h _b i krawędź - b. Formuły wiążące te ilości mają indywidualny wygląd dla odpowiedniej piramidy węglowej. Na przykład, dla regularnej piramidy, wysokość czworokątna może być określona przez formuły:

h = √ (a _b ² - a 2/4);

h = √ (b ² - a 2/2).

Te wzory wynikają z twierdzenia Pitagorasa, gdy rozważamy odpowiednie trójkąty prostokątne wewnątrz piramidy.

Jeżeli rozważa się figurę o podstawie trójkątnej, następujące formuły są ważne dla wysokości zwykłej piramidy:

h = √ (a _b ² - a 2/12);

h = √ (b ² - a 2/3).

Rozwiązanie problemu z piramidą sześciokątną

Załóżmy, że otrzymujemy regularną piramidę z sześciokątną podstawą. Wiadomo, że wysokość podstawy piramidy wynosi 13 cm, wiedząc, że długość jej bocznej krawędzi wynosi 10 cm, konieczne jest obliczenie objętości i wysokości regularnej piramidy sześciokątnej.

Poniższy rysunek pokazuje, jak wygląda zwykły sześciokąt.

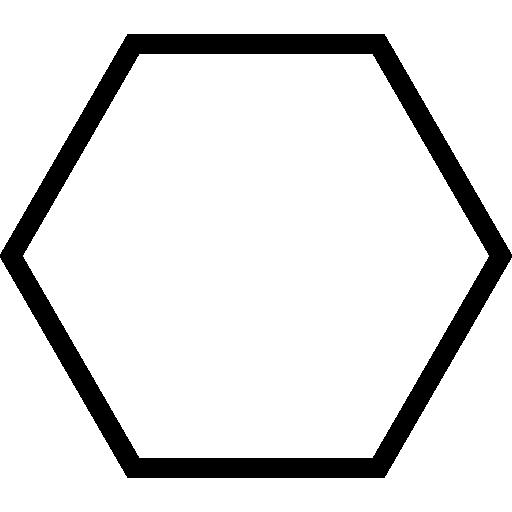
Odległość między dowolnymi dwoma równoległymi bokami nazywa się wysokością. Nietrudno wykazać, że ta wysokość h _a jest związana z długością boku figury z następującą formułą:

h _a = a * √3

Wstawiając wartość h do wyrażenia, stwierdzamy, że podstawowa strona a jest równa 7,51 cm.

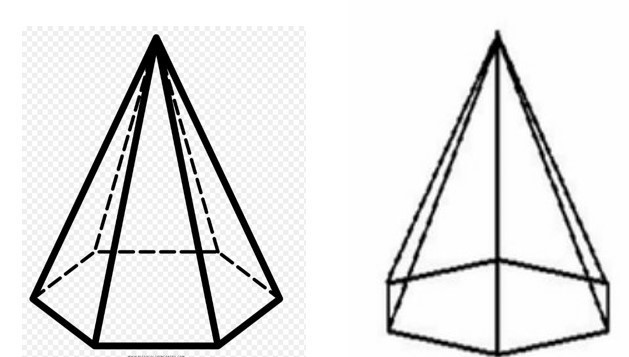
Wysokość h figury można określić, jeśli weźmiemy pod uwagę trójkąt prostokątny wewnątrz piramidy i składający się z dwóch nóg (wysokość piramidy i połowy przekątnej sześciokątnej podstawy) i przeciwprostokątnej (krawędź boczna). Wtedy wartość h będzie równa:

h = √ (b ² - a ² ) = √ (100 - 56,4) = 6,6 cm.

Objętość piramidy określa się jako trzecią część iloczynu wysokości figury na obszarze jego podstawy. Obszar zwykłego sześciokąta to:

S ₆ = n / 4 * a ² * ctg (pi / n) = 6/4 * a ² * ctg (pi / 6) = 3 * √ 3/2 * a ² = 3 * √ 3/2 * 56, 4 ≈ 146,53 cm ² .

Formuła użyta do obliczenia S6 jest uniwersalna dla dowolnego regularnego n-gon.

Aby określić objętość figury, należy zastąpić parametry znalezione we właściwej formule:

V = 1/3 * h * S ₆ = 1/3 * 6,6 * 146,53 = 322,366 cm ³ .

Uzyskaliśmy wartość wysokości piramidy i obliczyliśmy jej objętość. W ten sposób problem został rozwiązany.