Znaki podobieństwa trójkątów i ich praktyczne zastosowanie do rozwiązywania problemów

Pojęcie arbitralności jest arbitralne geometryczne kształty w istocie bardzo łatwo to wyjaśnić, a jeszcze mniej udowodnić. Na przykład, patrząc na obiekt przez szkło powiększające, widzimy obraz tego obiektu powiększony kilka razy z zachowaniem proporcji wszystkich jego wymiarów. Innymi słowy, obraz obiektu jest podobny do oryginalnego obiektu przed powiększeniem. W większości problemów geometrii, aby udowodnić proporcjonalność stron i obszary trójkąta zastosuj główne 3 znaki. Aby uwzględnić istniejące oznaki podobieństwa trójkątów, należy wstępnie zdefiniować kluczową koncepcję, która będzie stosowana w tekście w przyszłości.

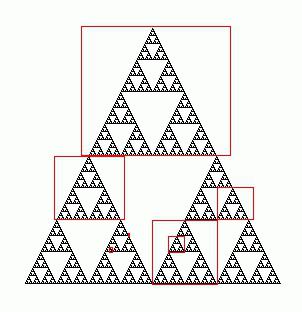
Tak więc, trójkąty są podobne, jeśli ich podobnie położone boki są proporcjonalne, a odpowiednio ułożone kąty są równe (warto pamiętać, że boki są nazywane podobnymi, lub odpowiadającymi, jeśli znajdują się naprzeciwko identycznych kątów). Rozważ podobne trójkąty ΔABC i ΔA1B1C1. Zgodnie z powyższą koncepcją odpowiednimi stronami są: AB i A1B1, a także pary boków BC i B1C1, AC i A1C1. Zauważ, że boki każdej z tych trzech par leżą naprzeciw przeciwnych kątów tej samej wielkości.

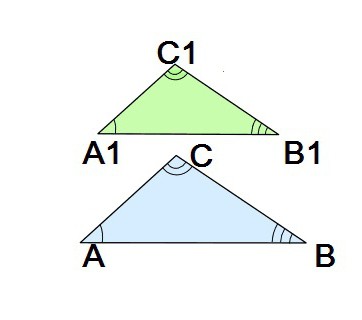Podobieństwo oznaczane jest przez specjalny charakter który jest umieszczony pomiędzy oznaczeniami danych liczb: ΔABC ~ ΔA1B1C1.

Stosunek odpowiednich stron z obecnością tej cechy jest parametrem zwanym współczynnikiem podobieństwa k. Jeśli k = 2, wówczas możemy powiedzieć, że jedna z dwu rozważanych figur geometrycznych jest powiększoną podwójną kopią drugiej. Oczywiste jest, że jeśli k = 1, to trójkąty są równe. Tak więc tę równość można uznać za szczególny przypadek ich podobieństwa.

Znaki podobieństwa trójkątów

Okazuje się, że w celu ustalenia obecności rozpatrywanej cechy nie ma potrzeby sprawdzania wszystkich wymagań wymienionych w sformułowaniu definicji podobieństwa podanej powyżej. Wystarczy spełnić minimalny zestaw warunków, a teraz to potwierdzimy w praktyce.

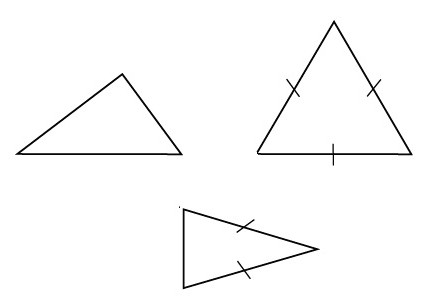
Pierwszy znak

Podczas rozwiązywania problemów pierwsza oznaka podobieństwa trójkątów pojawia się znacznie częściej niż pozostałe. Zwróć uwagę, że działa tylko z dwoma elementami figury geometrycznej: dwoma kątami. Pozostałe oznaki podobieństwa trójkątów wymagają udziału trzech elementów. Tak więc, dla dwóch dowolnie podobnych trójkątów, 2 kąty jednego z nich są równe tym samym 2 kątom drugiego.

Dowód

Zgodnie z podstawowymi właściwościami obowiązującymi dla dowolnego trójkąta, możemy zapisać następujące wyrażenie dla ∠C. Jego wartość będzie równa (180 ° - (∠А + ∠В)), dla innego ∠С ₁ wartość zostanie obliczona na tej samej zasadzie. Przez elementarne transformacje wyrażeń uzyskujemy ∠C = C ₁ . Zatem wszystkie kąty występujące w ΔАВС są równe wszystkim analogicznym kątom znajdującym się w ΔА ₁ В ₁ С ₁ . Według podobnego algorytmu udowodniono pozostałe objawy podobieństwa trójkątów.

Drugi znak

To podejście do dowodu jest często stosowane, jeśli znane są kąty rozpatrywanych figur geometrycznych.

W przypadku dwóch podobnych trójkątów prawdą jest, że 2 boki każdego z nich są proporcjonalne do 2. podobnych boków drugiego, a kąty między tymi parami boków są równe.

Dowód

Aby udowodnić tę funkcję, musisz odwołać się do poprzednich obliczeń. W oparciu o powyższe wyniki wystarczy udowodnić, że ∠В = В ₁ . Rozważmy ΔABC ₂ , dla którego, zgodnie z pierwszym znakiem, prawdziwe są następujące stwierdzenia: ∠1 = ∠А ₁ , ∠2 = В ₁ . ΔABC ₂ ~ ΔА ₁ В ₁ С ₁ . Oznacza to AB / A ₁ B ₁ = AC ₂ / A ₁ C. Z drugiej strony wiadomo, że obowiązuje następująca relacja: AC / A ₁ C _{1 =} AB / A ₁ B ₁ . W rezultacie otrzymujemy równość boków AC = AC ₂ , a także stwierdzenie, że ΔABC ~ ΔABC ₂ według drugiego znaku (AC = AC ₂ i ∠A = ∠1, ponieważ w wyniku uwzględnienia danych początkowych ustalono, że A = ∠A ₁ i ∠1 = ∠ A1, AB- jest wspólną stroną dla tych dwóch trójkątów). Z dowodu, że ∠B = ∠2, a od ∠2 = ∠В1, otrzymujemy ∠ = = ₁ . Z tego wynika, że ​​udowodniono inny znak.

Trzeci znak

Ta cecha jest uważana za najbardziej oczywistą, gdy dowodzi się podobieństwa, ponieważ wszystkie strony tych trójkątów o znanych parametrach są brane pod uwagę.

Tak więc, dla dwóch trójkątów, które są do siebie podobne, istnieje stwierdzenie, że 3 boki jednego z nich są proporcjonalne do 3 odpowiadających sobie boków drugiego.

Dowód

Biorąc pod uwagę poprzednią cechę podobieństwa, teraz dla skonstruowania dowodu wystarczy ustalić tylko, że istnieje równość formy: ∠A = ∠A ₁ . Aby to zrobić, rozważ dowolne ΔABC ₂ , dla którego ∠1 = ∠A ₁ , 2 = В ₁ . Według pierwszego atrybutu ΔABC ₂ ~ ΔA ₁ B ₁ C ₁ , więc dla tych dwóch trójkątów możemy zapisać stosunek typu AB / A ₁ B ₁ = BC ₂ / B1 C ₁ = C ₂ A / C ₁ A _1, z którego możemy napisać równość formy: B ₁ C ₁ = BC ₂ , A ₁ C ₁ = AC ₂ . Na tej podstawie logiczne jest stwierdzenie, że ΔABC ~ ΔABC ₂ i, na koniec, ∠A i ∠A ₁ są równe. Z tego wynika, że ​​rozpatrywana cecha jest również udowodniona.

Właściwości

1. Dla dwóch trójkątów, podobnych do siebie, stosunek wartości ich powierzchni jest wprost proporcjonalny do współczynnika do kwadratu. Dowód. Rozważ dwie arbitralne figury o trzech bokach i trzech kątach, które są do siebie podobne. Niech A i A ₁ będą odpowiednimi bokami tych figur, a h i h ₁ będą odpowiednimi wysokościami. Niech k będzie współczynnikiem podobieństwa dla rozpatrywanych trójkątów, dlatego ze współczynnika kształtu możemy zapisać równanie postaci: A ₁ = k * A. Łatwo zauważyć, że dla stosunku wysokości możemy zapisać równanie postaci: h ₁ = k * h. Dla stosunku powierzchni rozpatrywanych figur geometrycznych otrzymujemy: S ₁ / S = (1 / 2a ₁ h ₁ ) / (1 / 2ah) = (a ₁ / a) * (h ₁ / h) = k * k = k ² . Tak więc, gdy trójkąt jest "rozciągnięty" o 2 razy, jego powierzchnia wzrasta o 2 ² = 4 razy. Druga właściwość wynika z poprzedniego dowodu i jest bezpośrednio z nią powiązana.
2. Wszystkie odpowiadające linie rysowane w takich trójkątach są również proporcjonalne do siebie i równe wartości ujawnionego powyżej współczynnika. Oznacza to, że zgodnie z powyższą właściwością można argumentować, że wszystkie wewnętrzne konstrukcje dodatkowe będą również proporcjonalne.

Dodatek do głównej listy znaków

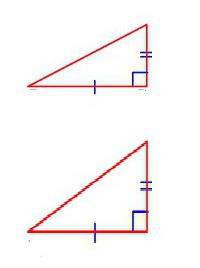
Warto rozważyć szereg indywidualnych cech, które mają zastosowanie do kształtów geometrycznych określonego typu. Więc trójkąty prostokątne są podobne, jeśli:

• ich przeciwprostokątna i dowolna z dwóch odnóg są odpowiednio proporcjonalne;
• jeżeli odpowiadające im ostre kąty są równe;
• jeśli wszystkie nogi rozpatrywanych trójkątów są proporcjonalne do pary.

Wniosek

W ten sposób połączyliśmy wszystkie możliwe znaki, za pomocą których można udowodnić podobieństwo dwóch lub więcej liczb z trzema rogami i bokami, niezależnie od ich rodzaju i właściwości. W większości problemów geometrycznych główne trzy znaki służą do udowodnienia proporcjonalności boków i obszarów, ale nie pominęliśmy wielu znaków podobieństwa, które mają zastosowanie tylko wtedy, gdy konieczne jest przeprowadzenie dowodu na dane geometryczne, o których mowa, pod kątem prostym. Te oznaki podobieństwa prawe trójkąty znacznie upraszczają proces rozwiązywania różnych zadań i wymagają dla nich minimum danych.