Niektóre informacje o kostce i jak obliczyć powierzchnię sześcianu
Kostka jest niesamowitą figurą. Tak samo jest ze wszystkich stron. Każda jego twarz może natychmiast stać się podstawą lub bokiem. I to niczego nie zmieni. A wzory do tego są zawsze łatwe do zapamiętania. I bez względu na to, co musisz znaleźć - objętość lub powierzchnia sześcianu. W tym ostatnim przypadku nie trzeba nawet uczyć się czegoś nowego. Wystarczy zapamiętać tylko kwadratową formułę.
Jaki jest obszar?
Wartość ta jest zwykle oznaczona literą łacińską S. Dotyczy to również przedmiotów szkolnych, takich jak fizyka i matematyka. Jest mierzony w kwadratowych jednostkach długości. Wszystko zależy od danych w wartościach problemu. Mogą to być mm, cm, m lub km do kwadratu. I są przypadki, kiedy jednostki nie są nawet wskazane. Jest to po prostu numeryczna ekspresja obszaru bez nazwy.
Więc jaki jest ten obszar? Jest to wielkość będąca liczbową charakterystyką danej figury lub bryły objętości. Pokazuje wielkość jego powierzchni, która jest ograniczona bokami figury.
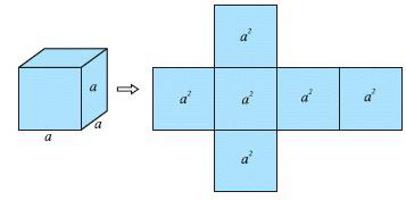
Jaki kształt nazywa się sześcianem?
Ta liczba jest wielościanem. I nie jest łatwe. Ma rację, to znaczy, że wszystkie elementy są sobie równe. Czy to boki, czy krawędzie. Każda powierzchnia sześcianu jest kwadratem.
Inną nazwą sześcianu jest regularny sześcian, jeśli w języku rosyjskim, a następnie sześciokąt. Może być utworzony z czworokątnego pryzmatu lub równoległościanu. Z zastrzeżeniem warunków, w których wszystkie krawędzie są równe, a kąty tworzą 90 stopni.
Ta liczba jest tak harmonijna, że często jest używana w życiu codziennym. Na przykład pierwsze zabawki tego dziecka to kostki. A zabawa dla osób starszych to Kostka Rubika.

W jaki sposób sześcian jest połączony z innymi kształtami i ciałami?
Jeśli narysujesz sekcję sześcianu przechodzącą przez trzy twarze, będzie to mieć rodzaj trójkąta. Wraz ze wzrostem odległości od wierzchołka, sekcja będzie się powiększać. Nadejdzie chwila, gdy 4 twarze się skrzyżują, a figura w sekcji stanie się czworoboczna. Jeśli przytrzymasz przekrój przez środek sześcianu, tak aby był prostopadły do jego głównych przekątnych, otrzymasz regularny sześciokąt.
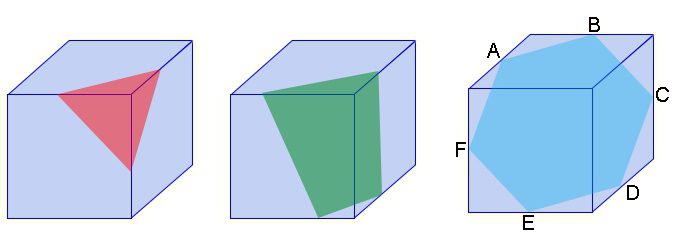
Wewnątrz kostki możesz narysować czworościan (trójkątną piramidę). Na czubek czworościanu bierze się jeden z jego rogów. Pozostałe trzy pokrywają się z wierzchołkami, które leżą na przeciwległych końcach krawędzi wybranego kąta sześcianu.
Możesz wpisać w nim ośmiościan (wypukły regularny wielościan, który wygląda jak dwie połączone piramidy). Aby to zrobić, znajdź centra wszystkich ścian sześcianu. Będą wierzchołkami ośmiościanu.
Odwrotna operacja jest również możliwa, to znaczy, że w ośmiościanie jest naprawdę możliwe wejście do sześcianu. Dopiero teraz centra twarzy pierwszego staną się wierzchołkami dla drugiego.
Metoda 1: Oblicz obszar sześcianu według jego krawędzi
Aby obliczyć całą powierzchnię sześcianu, wymagana jest znajomość jednego z jego elementów. Najprostszym sposobem rozwiązania jest, gdy znana jest jego krawędź lub, innymi słowy, strona kwadratu, z którego się składa. Zazwyczaj ta wartość jest oznaczona literą łacińską "a".
Teraz musimy przypomnieć formułę, według której obliczany jest kwadrat. Aby się nie pomylić, jego oznaczenie wprowadza litera S 1 .
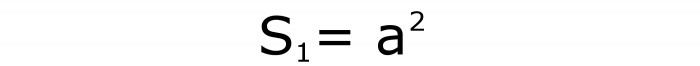
Dla wygody lepiej jest przypisać numery do wszystkich formuł. To będzie pierwsze.
Ale to tylko jeden kwadrat. Jest ich sześć: 4 na bokach i 2 na dole i na górze. Następnie powierzchnia sześcianu obliczana jest według następującego wzoru: S = 6 * a 2 . Jej liczba to 2.
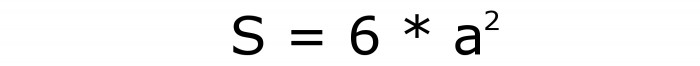
Metoda 2: Jak obliczyć obszar, jeśli znasz objętość ciała
Ta metoda sprowadza się do zliczania długości krawędzi o znaną objętość. A następnie użyj dobrze znanej formuły, która jest tutaj oznaczona numerem 2.
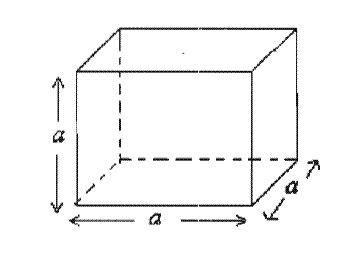
Z matematycznego wyrażenia dla objętości sześcianu można wyprowadzić jeden, za pomocą którego można obliczyć długość krawędzi. Oto ona:
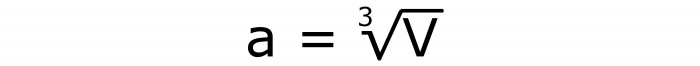
Numerowanie jest kontynuowane, a tutaj jest numer 3.
Teraz można go obliczyć i zastąpić drugą formułą. Jeśli działamy zgodnie z normami matematyki, musimy wyprowadzić następujące wyrażenie:
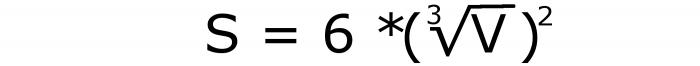
Jest to formuła dla obszaru całej powierzchni sześcianu, która może być użyta, jeśli znana jest objętość. Ten rekord to 4.
Metoda 3: obliczanie powierzchni na przekątnej sześcianu
Aby obliczyć powierzchnię całej powierzchni sześcianu, należy również narysować krawędź przez znaną przekątną. Używa wzoru na główny sześciokąt przekątny:
To jest wzór numer 5.
Z niego łatwo wyprowadzić wyrażenie dla krawędzi sześcianu:
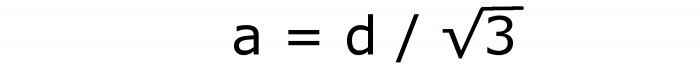
To jest szósta formuła. Po jego obliczeniu można ponownie użyć formuły pod drugim numerem. Ale lepiej jest napisać to:
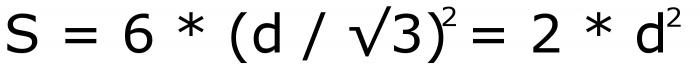
Okazuje się, że ma numer 7. Jeśli przyjrzysz się uważnie, zobaczysz, że ta ostatnia formuła jest wygodniejsza niż obliczenia etapowe.
Metoda 4: Jak wykorzystać promień wpisanego lub opisanego okręgu do obliczenia powierzchni sześcianu
Jeśli oznaczymy promień okręgu opisanego wokół sześcianu przez literę R, wówczas powierzchnia sześcianu będzie łatwo obliczona za pomocą następującej formuły:
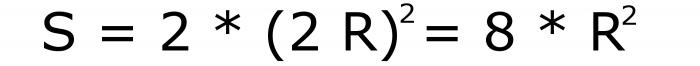
Jego numer seryjny to 8. Łatwo go uzyskać dzięki temu, że średnica koła całkowicie pokrywa się z główną przekątną.
Oznaczając promień wpisanego koła łacińską literą r, można uzyskać następującą formułę dla obszaru całej powierzchni sześcianu:
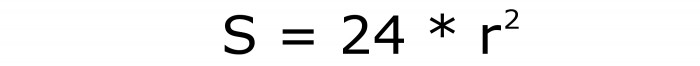
To jest wzór numer 9.
Kilka słów o bocznej powierzchni sześcianu
Jeśli problem wymaga znalezienia obszaru bocznej powierzchni sześcianu, musisz użyć techniki opisanej powyżej. Kiedy krawędź bryły jest już podana, to po prostu kwadrat kwadratu musi zostać pomnożony przez 4. Ta figura pojawiła się, ponieważ istnieją tylko 4 boczne ściany sześcianu.Mata matematyczna dla tego wyrażenia jest:

Jej liczba to 10. Jeśli podane są inne wartości, wykonaj to samo, co metody opisane powyżej.
Przykłady zadań
Stan pierwszego. Znana powierzchnia sześcianu. Ma 200 cm². Konieczne jest obliczenie głównej przekątnej sześcianu.
Decyzja.
1 sposób. Konieczne jest użycie formuły oznaczonej numerem 2. Z niej łatwo będzie wywnioskować "i". Ta notacja matematyczna będzie wyglądać pierwiastek kwadratowy od częściowej równej S przez 6. Po zastąpieniu liczb otrzymujemy:
a = √ (200/6) = √ (100/3) = 10 √3 (cm).
Piąta formuła pozwala natychmiast obliczyć główną przekątną sześcianu. Aby to zrobić, musisz pomnożyć wartość krawędzi przez √3. To jest proste. Odpowiedź jest taka, że przekątna wynosi 10 cm.
2 sposób. W przypadku zapomnienia wzoru na przekątną, ale pamiętam twierdzenie Pitagorasa.
W ten sam sposób, jak w pierwszej metodzie, znajdź krawędź. Następnie musisz dwukrotnie zapisać twierdzenie dla przeciwprostokątnej: pierwsza dla trójkąta na twarzy, druga dla tego, która zawiera pożądaną przekątną.
х² = а² + а², gdzie x to przekątna kwadratu.
d² = x² + a² = a² + a² + a² = 3 a². Z tego zapisu łatwo jest zobaczyć, w jaki sposób uzyskano formułę przekątnej. A potem wszystkie obliczenia będą, tak jak w pierwszej metodzie. Trochę dłużej, ale pozwala nie zapamiętać formuły, ale ją zdobyć samodzielnie.
Odpowiedź: przekątna sześcianu równa 10 cm.
Drugi warunek. Dla znanej powierzchni, która jest równa 54 cm 2 , obliczyć objętość sześcianu.
Decyzja.
Używając formuły pod drugim numerem, musisz znać wartość krawędzi kostki. Sposób wykonania tej czynności opisano szczegółowo w pierwszej metodzie rozwiązania poprzedniego problemu. Po wszystkich obliczeniach otrzymujemy, że a = 3 cm.
Teraz musisz użyć wzoru na objętość sześcianu, w którym długość krawędzi jest podnoszona do trzeciej potęgi. W związku z tym objętość będzie uważana za: V = 3 3 = 27 cm 3 .
Odpowiedź: objętość kostki wynosi 27 cm 3 .

Stan trzeciego. Wymagane jest znalezienie krawędzi kostki, dla której spełniony jest następujący warunek. Kiedy krawędź zostanie zwiększona o 9 jednostek, powierzchnia całej powierzchni powiększy się o 594.
Decyzja.
Ponieważ nie ma wyraźnych liczb w problemie, tylko różnica między tym, co było i co się stało, należy wprowadzić dodatkowe oznaczenia. To łatwe. Niech żądana wartość będzie równa "a". Następnie powiększona krawędź sześcianu będzie (a + 9).
Wiedząc o tym, musisz dwukrotnie zapisać wzór na powierzchnię sześcianu. Pierwszy - dla początkowej wartości krawędzi - pokryje się z numerem ponumerowanym numerem 2. Drugi będzie się nieco różnić. W jego miejsce zamiast "a" musisz zapisać kwotę (a + 9). Ponieważ problem dotyczy różnicy obszarów, musimy odjąć mniejszy obszar od większego obszaru:
6 * (a + 9) 2 - 6 * a 2 = 594.
Konieczne jest przeprowadzenie transformacji. Najpierw wypuść 6 w lewej części równości, a następnie uprość to, co pozostało w nawiasach. Mianowicie (a + 9) 2 - a 2 . Oto różnica kwadratów, które można przekształcić w następujący sposób: (a + 9 - a) (a + 9 + a). Po uproszczeniu wyrażenia uzyskujemy 9 (2a + 9).
Teraz musi zostać pomnożona przez 6, czyli liczbę, która była przed nawiasem, i utożsamiana z 594: 54 (2a + 9) = 594. To równanie liniowe z jednym nieznanym. Łatwo go rozwiązać. Najpierw należy otworzyć nawiasy, a następnie przenieść addendum o nieznanej wartości po lewej stronie równania, a liczby po prawej stronie. Równanie się wyjaśni: 2а = 2. Widać stąd, że wymagany rozmiar jest równy 1.
Odpowiedź: a = 1.