Pojęcie macierzy i podstawowe definicje

Taka koncepcja, jak macierz, jest używana i pojawia się w sekcjach wyższej matematyki. Najczęściej znajduje się w układzie równań liniowych. Więc jaka jest podstawowa koncepcja macierzy? Aby to zrozumieć, nie trzeba być geniuszem matematycznym.

Macierz to coś, co jest układem liczb mn, które w matematyce zapisywane są w postaci tabel, w których m to rzędy, a n to kolumny. Na jego przecięciu są elementy. Rozmiar macierzy zależy od liczby wierszy i kolumn.

Początkowo rozważano macierz trójkątną, ale nie jest to wygodne do rozwiązywania złożonych równań, dlatego w matematyce stosuje się prostokątny analog. Taki system uważa się za dogodny do rozwiązania problemu.

Skąd wzięła się matryca

Jeśli mówimy o pierwszej wzmiance, pojęcie matrycy pochodziło z Chin, a raczej było związane z "magicznymi kwadratami". Tabele te zostały uznane za amulety ze względu na wpisane liczby. W tym czasie nie było ani samej koncepcji matrycy, ani sposobów jej rozwiązania. W niektórych plemionach określała stopień pokrewieństwa, aby ludzie dowiedzieli się, czy mogą wyjść za mąż czy nie.

Ale sama koncepcja została wprowadzona na początku XIX wieku przez Jamesa Sylvestera, angielskiego matematyka. Różni naukowcy pracowali nad teorią macierzy, tworząc kompleks rozwiązań dla trudnych problemów algebraicznych.

Macierz i jej główne typy

Tak więc wcześniej rozważano pojęcie matrycy. Rodzaje matryc przedstawiono poniżej:

• Małe litery Składa się z pojedynczego wiersza, to jest tego typu macierz ma liczbę wierszy dokładnie m = 1, ale liczba jego kolumn jest dowolna.
• Kolumnowy. Ta odmiana składa się tylko z jednej kolumny, ale może również zawierać kilka wierszy. Dla tego rodzaju matrycy ma swój własny uniwersalny wpis. Wskazuje, że elementy w nawiasach powinny być zapisane jako kolumny. Co więcej, oszczędza nie tylko przestrzeń, ale i czas.
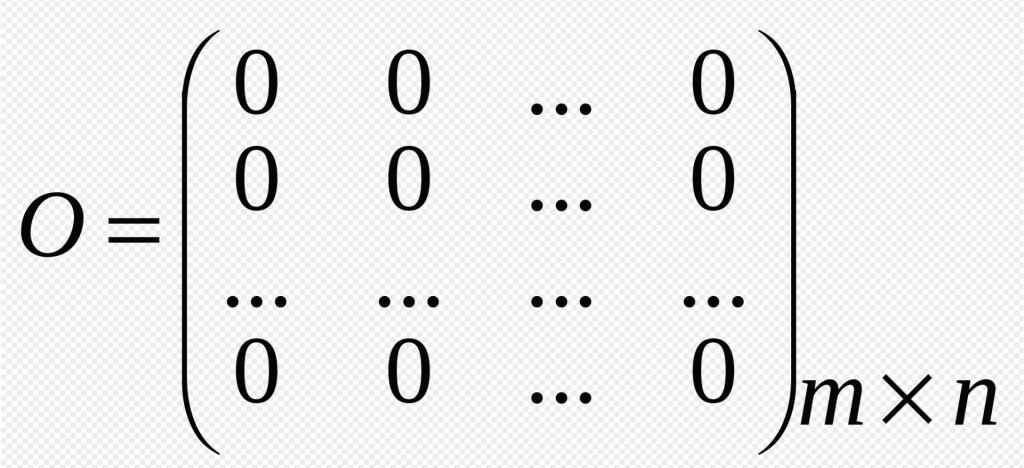
• Macierz zerowa Ta forma istnieje, gdy wszystkie jej elementy są równe 0. Oznaczają one ten typ macierzy "O" Ten element również otrzymał swoją nazwę ze względu na fakt, że w rachunku ma podobne funkcje z zerową teorią liczb.
• Kwadrat. Ten rodzaj matrycy jest najbardziej powszechny, a różnica polega na tym, że ma on taką samą liczbę kolumn i wierszy. Kiedy dwa elementy są połączone na różnych końcach kolumny, otrzymujemy główną przekątną. Pod tym względem stół przekątny dzieli się na kilka systemów:

a) Przekątna. Ten typ macierzy kwadratowej, który nie zawiera elementów należących do głównej przekątnej.

b) Single. Ten typ przekątnej składa się tylko z jednej jednostki. W tym wszystkim każda taka matryca jest skalarna.

c) Skalar. Jest to typ, w którym główna przekątna składa się z tej samej liczby.

d) Strzałka. Jest to rodzaj kwadratowej macierzy, w której prawie wszystkie elementy są zerowe, ale komponenty tworzące pierwszą kolumnę, a także te związane z przekątną i pierwszym rzędem, nie są równe.

• Binarny Ten typ tabeli składa się z zer i jedynek.
• Matryca Pascala - w tym rodzaju macierzy wszystkie elementy składają się z liczb należących do trójkąta o tej samej nazwie.
• Tridiagonal W tego rodzaju matrycy niezerowe elementy znajdują się na trzech przekątnych, które obejmują główną i te powyżej i poniżej.

Macierz rangi

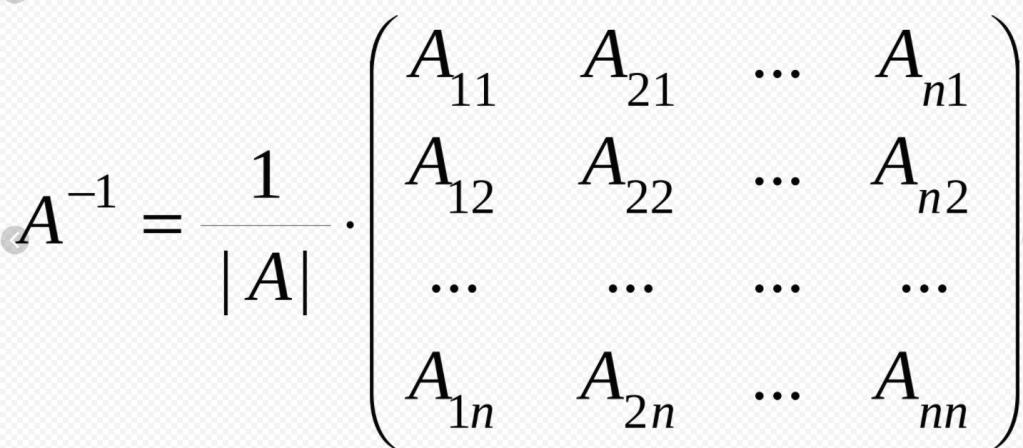
Dowiedziawszy się, że ma on różne typy, należy powiedzieć o następującej koncepcji: o randze macierzy. Rozumie się przez to liczbę niezależnych kolumn liniowych lub liczbę niezależnych rzędów liniowych. Również ranga każdej matrycy jest rzędem nieletnich, który jest najwyższy, jego wyznacznik jest niezerowy.

Ranga jest wskazywana przez rang A, ale ranga A. Oba pojęcia są uważane za poprawne, więc przy różnych pisowni nie będzie to uważane za błąd. Najważniejsze jest, aby nie zapominać, że rząd wierszy jest zawsze równy rzędowi kolumn.

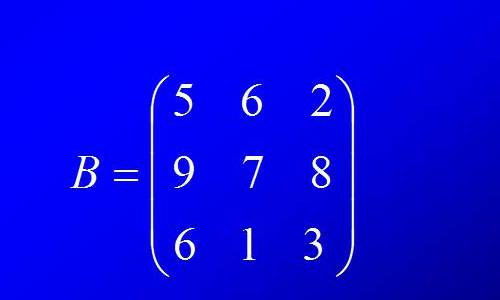
Akcje na macierzy

Macierz jest uniwersalnym systemem rozwiązywania problemów algebraicznych, na którym wykonywane są różne akcje. Obejmują one mnożenie dwóch macierzy, dodawanie, mnożenie przez liczbę i inne macierze.

Wykonywanie licznych akcji w algebrze umożliwia systemowi różnych macierzy łatwiejsze rozwiązywanie problemów. Zajmuje mniej czasu i pomaga nie gubić się w wielu akcjach.

Operacje związane z macierzami są wykorzystywane nie tylko w matematyce, ale także w fizyce i chemii.