Prawa optyki geometrycznej i ich zastosowanie w lustrze sferycznym i cienkich soczewkach
Zachowanie promieni świetlnych podczas przechodzenia przez różne przezroczyste media może być jednoznacznie określone bez znajomości natury samego światła. Takie zadania są obsługiwane przez specjalną gałąź fizyki - optykę geometryczną. Jego prawa są rozważane w tym artykule.
Właściwości promieni świetlnych w optyce geometrycznej
Poprzez właściwości promieni w tej sekcji fizycy rozumieją specyfikę ich ruchu w przezroczystych mediach. W szczególności, podczas przesuwania wiązki światła w homogenicznym medium, następujące stwierdzenia są prawdziwe:
- ścieżka światła jest linią prostą;
- przecinające się dwie wiązki światła nie współdziałają ze sobą;
- medium materialne określa prędkość światła w nim.
Te właściwości są fundamentalne dla każdej fali elektromagnetycznej. Dzięki nim powstają podstawowe prawa optyki geometrycznej dla zjawisk:
- odbicia;
- załamanie
Zasada farmy
W rzeczywistości jest to bezpośrednią konsekwencją prawa prostoliniowej propagacji światła w jednorodnym przezroczystym materiale. Zasada ta stanowi, że światło podczas procesów odbicia i załamania wybiera taką trajektorię z jednego punktu do drugiego w przestrzeni, którą może pokonać w najkrótszym czasie.
Zasada najmniejszego czasu została sformułowana przez francuskiego naukowca Pierre'a Fermata na początku lat sześćdziesiątych XVI wieku. Zgodnie z zasadą Fermata, prawa optyki geometrycznej związane ze zjawiskiem załamania i odbicia otrzymały matematyczny uzasadnienie. Ciekawe jest, że te prawa były już znane od XVII wieku. Co się tyczy Pierre'a Fermata, chociaż znana zasada najkrótszego czasu nosi jego imię, został sformułowany na długo przed Francuzem (przynajmniej z powodu zjawiska refleksji). Dokonał tego grecki egipski filozof Heron z Aleksandrii w pierwszym wieku naszej ery.
Z zasady Fermata wynika jednoznacznie, że w jednorodnym medium światło musi poruszać się prostą drogą (prawo prostoliniowego rozchodzenia się światła). Jeśli medium nie jest jednorodne, światło będzie się rozprzestrzeniać wzdłuż pewnej krzywej, ale zasada najkrótszego czasu nie zostanie naruszona. Używając go, można łatwo wyprowadzić formulacje matematyczne dla zjawisk odbicia i załamania, które uzyskano przez uogólnienie dużej ilości materiału doświadczalnego.
Ad
Procesy refrakcji i odbicia światła i ich matematyczny opis

Oba te zjawiska charakteryzują się tym, że wiązka światła w jednym punkcie drastycznie zmienia trajektorię. Dzieje się tak, ponieważ w tym momencie napotyka przeszkodę na swojej drodze. Jeśli ta przeszkoda jest nieprzejrzystym materiałem, następuje pojedynczy proces odbicia. Jeśli przeszkoda jest przezroczysta, to oprócz odbijanej wiązki pojawia się również załamany.
Załóżmy, że przeszkodą jest płaska powierzchnia. Pozwól mu oddzielić dwa przezroczyste nośniki. Przez punkt padania promienia na powierzchnię rysujemy prostopadle do niego (normalny N). Wektor promienia padającego jest oznaczony przez r 1 ¯, wektor odbijanego promienia to r 2 ¯, a załamany to r 3 ¯. Kąt między r 1 ¯ i N jest oznaczany jako θ 1 , między r 2 ¯ i N - θ 2 , a na końcu między r 3 ¯ i N - θ 3 . Eksperymentalnie ustalono następujące zależności:
Ad
- Wektor promieni r 1 ¯, r 2 ¯, r 3 ¯ i prostopadły N leżą w tej samej płaszczyźnie.
- Kąt padania θ 1 i kąt odbicia θ 2 są sobie równe.
- Kąt załamania θ 3 jest związany z θ 1 przez relację n 1 * sin (θ 1 ) = n 2 * sin (θ 3 ).
Ta formuła nosi nazwę prawa Snella na cześć holenderskiego naukowca Willebrorda Snella. Snell sam otrzymał to pod względem odległości. Za pośrednictwem zatok w rogach zapisał go nieco później Rene Descartes, dlatego w krajach francuskojęzycznych nazywa się to prawem Snell-Descartesa. Symbole n 1 i n 2 są absolutnymi współczynnikami załamania światła ośrodka, które są określane przez stosunek prędkości światła w próżni do prędkości w odpowiednim materiale.
Relacje te nazywane są zwykle prawami odbicia i załamania optyki geometrycznej.
Lustra płaskie i sferyczne
Prawo prostoliniowej propagacji światła i prawa odbicia stosuje się do geometrycznych konstrukcji obrazów w lustrze. W tym przypadku lustra mogą być nie tylko płaskie, ale także wypukłe i wklęsłe.
Ad
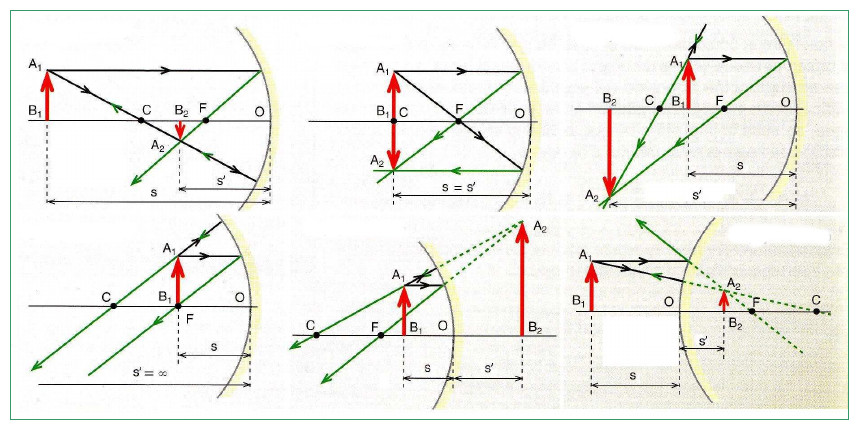
Nauka budowania niezależnie obrazów w lustrach dowolnego typu jest łatwa. Trzeba tylko zrozumieć, w jaki sposób promienie wchodzą w interakcję z urządzeniem optycznym. Zatem wiązka pochodząca z ogniska jest zawsze odbijana przez lustro równoległe do osi optycznej, a wiązka przechodząca przez środek lustra (wzdłuż promienia) jest odbijana w przeciwnym kierunku.
Różne przypadki położenia obiektu względem urządzenia optycznego i techniki budowania obrazów w lusterkach wklęsłych i wypukłych pokazano na poniższym rysunku.
Cienkie soczewki
To kolejne urządzenie optyczne, którego zasada opiera się na podstawowych prawach optyki geometrycznej. Cienka soczewka to obiekt wykonany z przezroczystego materiału i ograniczony dwiema powierzchniami. Jedna z powierzchni musi być segmentem kuli.
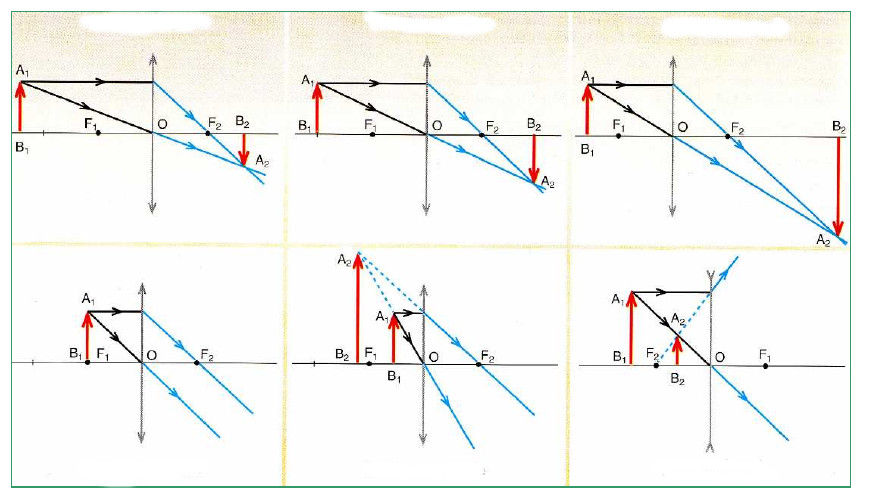
Obiektywy zbierają się (równoległe promienie skupiają się w ognisku za soczewką) i rozpraszają się (wyobrażone ciągłe równoległe promienie zbiegają się w ognisku przed obiektywem).
Zasada budowania w nich obrazów jest prawie taka sama jak w lusterkach sferycznych. Różne przypadki pokazano na poniższym rysunku.
Oko jako urządzenie optyczne
Między innymi, prawa optyki geometrycznej są wykorzystywane do badania zasady ludzkiego oka i dostosowania widzenia.

Oko jest złożonym układem optycznym z siłą dodatnią, to znaczy może być zastąpione równoważną soczewką zbierającą. Jeżeli umiejscowienie oka jest upośledzone (akomodacja prowadzi do zmiany mocy optycznej oka, w szczególności soczewki), wówczas na siatkówce powstaje niewyraźny obraz, przesuwając ostrość poza siatkówkę (dalekowzroczność) lub do przodu (krótkowzroczność). Korekta polega na dodawaniu (odejmowaniu) dioptrii do układu ocznego, aby przywrócić ostrość do siatkówki. Aby to zrobić, użyj okularów, soczewek lub laserowej korekcji wzroku.