Obwód kwadratu i prostokąta. Metody określania i przykłady rozwiązań.

Często w internecie można znaleźć wyśmiewanie się z tego, że wiedza z zakresu matematyki - całki, dyferencjały, funkcje trygonometryczne i inne sekcje przedmiotu - nie pomagają złagodzić życia danej osoby. Takie dowcipy są daremne, ponieważ pomagają poprawnie obliczyć obwód kwadratu, prostokąta i innych geometrycznych kształtów w pracach budowlanych. Zużycie materiału: płytki, tapety, podłogi - nie można określić bez zrozumienia podstawowych wzorów matematycznych i kształtów geometrycznych.

Właściwości kwadratowe

Wszelkie obliczenia matematyczne opierają się na właściwościach obiektu. Aby odpowiedzieć na pytanie: "Jaki jest obwód kwadratu?" - zaleca się przywołać charakterystyczne cechy tej figury.

1. Równość wszystkich stron.
2. Obecność czterech kątów 90 stopni.
3. Równoległość stron.
4. Symetria obrotu. Kiedy rysunek się obraca, jego wygląd pozostaje niezmieniony.
5. Umiejętność opisywania i wchodzenia do kręgu.
6. Przekątne na skrzyżowaniu dzielą się na pół.
7. Obszar postaci charakteryzuje przestrzeń wypełnioną kwadratem w przestrzeni dwuwymiarowej.
8. Obwód figury to nic innego, jak suma długości boków.
9. Z poprzedniej własności wynika, że ​​jednostkami miary obwodu będą jednostki długości: m, cm, dm i inne.

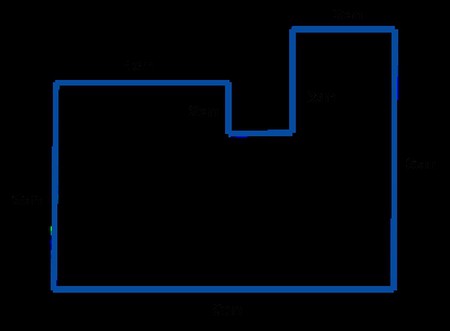
Aby policzyć listwy przypodłogowe, by dokonać napraw w kwadratowym pokoju, musisz znać długość pokoju. Aby to zrobić, obliczyć jego obwód.

Obwód

Przetłumaczone z greckiego słowa oznacza "miara wokół". Termin odnosi się do wszystkich zamkniętych kształtów: kwadrat, koło, prostokąt, trójkąt, trapez i inne. Znajomość definicji obwodu elementarnych figur jest potrzebna do rozwiązywania złożonych problemów geometrycznych z obiektami o nieregularnym kształcie. Na przykład, aby obliczyć cokoły w pomieszczeniu z układem typu "G", lub jak to jest również nazywane "ładowaniem", konieczne będzie określenie obwodu kwadratu i prostokąta. W końcu kształt pokoju składa się z tych elementarnych postaci.

Standardowym oznaczeniem takiej wielkości jest litera R. Każda figura, biorąc pod uwagę jej właściwości, ma swoją własną formułę wyznaczania obwodu.

Właściwości prostokąta

1. Równość przeciwnych stron.
2. Równość przekątnych.
3. Umiejętność opisania koła.
4. Wysokości prostokąta są równe bokom.
5. Suma kątów wynosi 360 stopni, a wszystkie kąty są prawidłowe.
6. Równoległość przeciwnych stron.
7. Prostopadłość sąsiednich boków.
8. Suma kwadratów przekątnych prostokąta jest równa sumie kwadratów jego boków.
9. Przecinając się, przekątne dzielą się na pół.
10. Niemożność dopasowania koła w kształcie.

Plac obwodowy

W zależności od ustalonych (znanych) parametrów kwadratu, istnieją różne formuły wyznaczania jego obwodu. Prostym zadaniem jest obliczenie obwodu na ustalonej długości jego boku (ów). W tym przypadku: Р = с + с + с + с lub 4 * с. Na przykład długość boku kwadratu wynosi 7 cm, a obwód figury będzie wynosił 28 cm (4 * 7).

W pierwszym przypadku wszystko jest jasne, ale jak znaleźć obwód kwadrat, znając jego obszar? I tutaj wszystko jest bardzo jasne. Ponieważ powierzchnia figury jest określona przez pomnożenie jednej strony przez drugą, a wszystkie strony są równe na kwadracie, konieczne jest wyodrębnienie korzenia ze znanej wartości. Przykład: jest kwadrat o powierzchni 25 dm ² . Korzeń 25 wynosi 5 - ta wartość charakteryzuje długość boku kwadratu. Teraz, zastępując znalezioną wartość - 5 dm ² - oryginalną formułą obwodu, możemy rozwiązać problem. Odpowiedź będzie miała wartość 20 dm. Oznacza to, że 4 pomnożone przez 5, otrzymało pożądaną wartość.

Kwadrat i koło

Z właściwości rozpatrywanej figury wynika, że ​​okrąg może być wpisany w kwadrat, a także być opisany wokół figury.

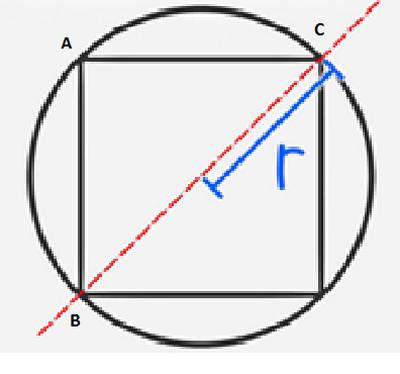
Pierwsza opcja polega na znalezieniu obwodu na obwodzie circumcircle. Napisany jest kwadrat, którego wierzchołki znajdują się na okręgu. Promień okręgu jest 1/2 długości przekątnej. Okazuje się, że średnica jest równa przekątnej. Teraz musisz wziąć pod uwagę trójkąt prostokątny co było wynikiem podziału przekątnej kwadratu. Rozwiązanie problemu ogranicza się do znalezienia boków tego trójkąta. BC jest znaną wartością, średnicą circumcircle. Załóżmy, że jest równa 3 cm. Twierdzenie Pitagorasa w przypadku równych boków trójkąta będzie wyglądać tak: 2c ² = 3 ² . We wzorze: symbol с jest długością boku trójkąta i kwadratu; 3 - znaną wartość przeciwprostokątnej. Stąd c = √9 / 2. Znając bok kwadratu, jego obwód nie jest problemem do obliczenia.

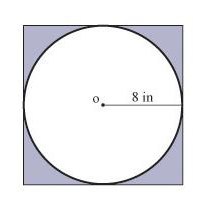
Cechą wpisanego koła jest podział boków kwadratu na pół. Dlatego promień jest równy połowie długości boku kwadratu. Następnie bok c = 2 * promień. Obwód kwadratu w tym przypadku to promień 4 * 2 * lub 8 promieni koła.

Prostokąt obwodu

Najbardziej elementarna formuła wyznaczania obwodu prostokąta poprzez znane wartości jego boków jest następująca: P = 2 (a + b), gdzie a i b są długością boków figury.

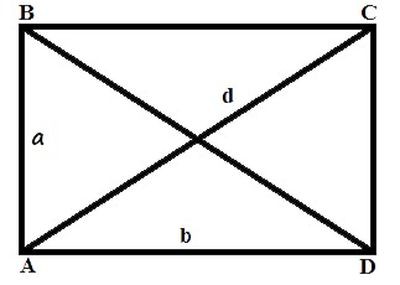
Przekątna prostokąta, podobna do kwadratu, dzieli figurę na pół, tworząc trójkąt prostokątny. Jednak zadanie to komplikuje fakt, że boki tego trójkąta są nierówne. W przypadku znanej wartości jednego z boków i przekątnej, drugi można znaleźć na podstawie twierdzenia Pitagorasa: d ² = a ² + w ² , gdzie a i v są bokami figury, a d jest przekątną.

Jeśli żadna ze stron nie jest znana, do gry wchodzi wiedza o trygonometrii: sinusy, cosinusy i inne funkcje.

Znalezienie obwodu wzdłuż opisanego okręgu i znanej średnicy jest zredukowane do faktu, że średnica jest równa długości przekątnej figury. Co więcej, rozwiązanie problemu zależy od obecności znanych ilości. Jeśli podane są kąty, to przez funkcje trygonometryczne. Jeśli zostanie podana strona, odpowiedź zostanie znaleziona za pomocą twierdzenia Pitagorasa.

Funkcje prostokąta i trygonometryczne

Dla jasności, przykład rozwiązania problemu. Biorąc pod uwagę: prostokąt AVSD; długość przekątnej ( d ) 20 cm; kąt f - 30 °. Znajdź obwód cyfry.

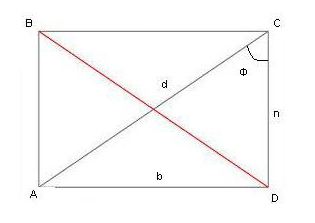
Od trygonometrii należy przypomnieć następujące: sinus kąta w trójkącie prostokątnym jest równy stosunkowi przeciwnej nogi do przeciwprostokątnej. Sinus 30 ° (są tabele, za pomocą których można określić wartości funkcji trygonometrycznych dla prawidłowych kątów) wynosi 1/2. Okazuje się, że 1/2 = stosunek do d . Nieznana wartość in będzie równa d / 2 = 20/2 = 10 cm.

Aby obliczyć obwód, powinieneś znaleźć drugą stronę figury. Jest to możliwe dzięki twierdzeniu Pitagorasa, ponieważ znane są długości przeciwprostokątnej i jednej z nóg, lub ponownie przez współczynnik kształtu dla cosinusa kąta.

Cosinus kąta φ jest wyrażony jako stosunek sąsiedniej nogi do przeciwprostokątnej i jest równy √3 / 2.

√3 / 2 = n / d , n = (d * √3) / 2 lub 10 * √3. Po wyjęciu korzenia z 3, otrzymujemy długość boków trójkąta: 10 * 1,73 = 17,3 cm.

Obwód wynosi 2 (17,3 + 10) = 2 * 27,3 = 54,6 cm.

Obwód i postawa

W programie szkolnym występują problemy z geometrią, gdy długości boków prostokąta wyrażają się wzajemnie. Rozpatrzenie rozwiązania tego problemu przedstawiono poniżej.

Wiadomo, że suma długości wszystkich boków prostokąta, czyli jego obwodu, wynosi 84 cm, a stosunek długości (d) do szerokości (w) wynosi 3: 2. Znajdź boki rysunku.

Rozwiązanie: niech długość będzie 3x, a szerokość 2x, zależnie od relacji od stanu problemu. Wzór obwodu prostokąta z danymi długości boków będzie następujący: 3x + 3x + 2x + 2x = 84. Dalej, 10x = 84, x = 8,4 cm. Poprzez podstawienie x do wyrażenia długości i szerokości prostokąta można znaleźć żądane wartości. Długość będzie: 3 * 8,4 = 25,2 cm; szerokość: 2 * 8,4 = 16,8 cm.

Artykuł poświęcony jest rozwiązywaniu najczęściej spotykanych zadań w szkolnym programie nauczania. A to nie wszystkie sposoby na znalezienie obwodu kwadratu i prostokąta.