Zasady, według których dodaje się wektory

W jaki sposób dodaje się wektory, nie zawsze jest jasne dla uczniów. Dzieci nie reprezentują tego, co kryje się za nimi. Musisz tylko zapamiętać zasady i nie zastanawiać się nad istotą. Dlatego chodzi o zasady dodawania i odejmowania wielkości wektorowych, które wymagają dużej wiedzy.

W wyniku dodania dwóch lub więcej wektorów zawsze uzyskuje się jeden. Co więcej, zawsze będzie to samo, niezależnie od odbioru jego lokalizacji.

Najczęściej w szkolnym kursie geometrii uważa się dodanie dwóch wektorów. Można go wykonać za pomocą reguły trójkąta lub równoległoboku. Te zdjęcia wyglądają inaczej, ale efekt działania jest jeden.

W jaki sposób dodaje się regułę trójkąta?

Jest używany, gdy wektory nie są współliniowe. Oznacza to, że nie należy leżeć na jednej linii ani na liniach równoległych.

W takim przypadku pierwszy wektor powinien zostać odłożony z jakiegoś dowolnego punktu. Od jego końca wymagane jest równoległe i równe drugiemu. Rezultatem będzie wektor pochodzący od początku pierwszego i kończący się na końcu drugiego. Figura przypomina trójkąt. Stąd nazwa reguły.

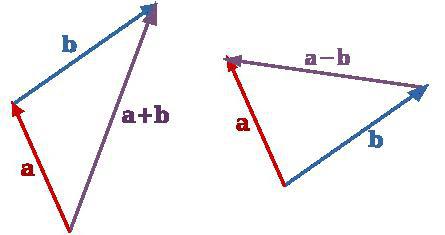
Jeśli wektory są współliniowe, wówczas można również zastosować tę regułę. Tylko rysunek będzie zlokalizowany wzdłuż jednej linii.

W jaki sposób dodatek jest zgodny z regułą równoległoboku?

Znowu? dotyczy tylko wektorów nieliniowych. Konstrukcja odbywa się na innej zasadzie. Chociaż początek jest taki sam. Konieczne jest odroczenie pierwszego wektora. A od początku - drugi. Na ich podstawie uzupełnij równoległobok i narysuj przekątną od początku obu wektorów. Ona będzie wynikiem. W ten sposób dodajemy wektory zgodnie z regułą równoległoboku.

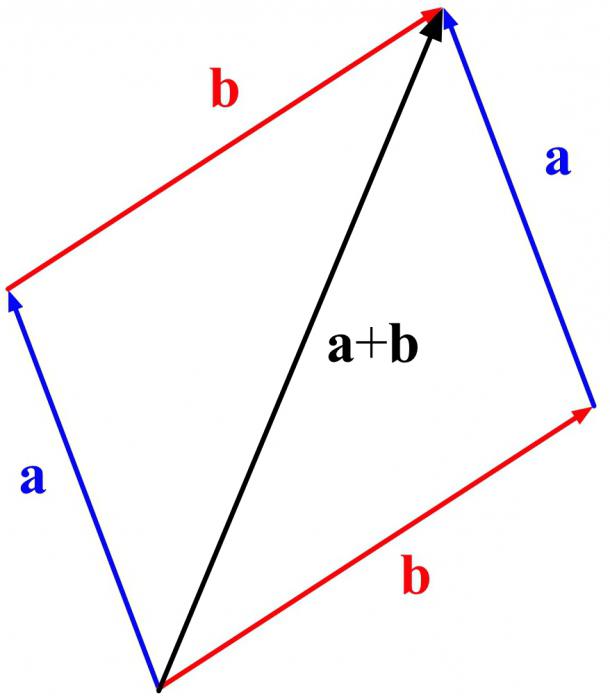
Do tej pory były dwa. A co, jeśli są 3 lub 10? Użyj następującej sztuczki.

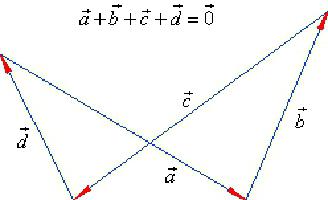
Jak i kiedy obowiązuje reguła wieloboku?

Jeśli chcesz wykonać dodanie wektorów, których liczba jest większa niż dwie, nie powinieneś się bać. Wystarczy odłożyć je wszystkie sekwencyjnie i połączyć początek łańcucha z jego końcem. Ten wektor będzie żądaną sumą.

Jakie właściwości są poprawne w przypadku działań z wektorami?

O zerowym wektorze. Który twierdzi, że po dodaniu go otrzymuje się oryginał.

Na przeciwległym wektorze. Oznacza to, że ma on kierunek przeciwny i jest równy wielkości do wartości. Ich suma będzie równa zeru.

O komutatywności dodatku. Co wiadomo od czasów szkoły podstawowej. Zmiana miejsc przedmiotów nie zmienia wyniku. Innymi słowy, bez względu na to, który wektor odkładać jako pierwszy. Odpowiedź będzie nadal poprawna i unikalna.

Na temat asocjacji dodawania. To prawo pozwala dodawać pary dowolnych wektorów z potrójnego i dodawać do nich trzeci. Jeśli napiszesz to za pomocą znaków, otrzymasz:

first + (second + third) = second + (first + third) = third + (first + second).

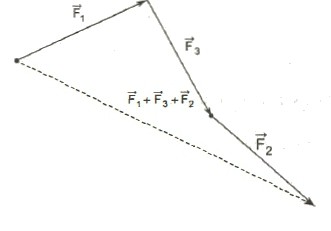
Co wiadomo o różnicy wektorów?

Odrębna operacja odejmowania nie istnieje. Wynika to z faktu, że w rzeczywistości jest dodatkiem. Tylko drugi z nich otrzymuje odwrotny kierunek. A potem wszystko odbywa się tak, jakby rozważano dodanie wektora. Dlatego praktycznie nie mówią o swoich różnicach.

Aby uprościć pracę z ich odejmowaniem, zmodyfikowano regułę trójkąta. Teraz (po odjęciu) drugi wektor musi zostać przesunięty od początku pierwszego. Odpowiedzią będzie ta, która łączy z nią punkt końcowy odliczenia. Chociaż możesz odkładać, jak opisano wcześniej, po prostu zmieniając kierunek drugiego.

Jak znaleźć sumę i różnicę wektorów we współrzędnych?

Problem podaje współrzędne wektorów i musisz znać ich wartości w finale. W tej konstrukcji nie trzeba wykonywać. Oznacza to, że możesz użyć prostych formuł, które opisują regułę dodawania wektorów. Wyglądają tak:

a (x, y, z) + in (k, l, m) = c (x + k, y + 1, z + m);

a (x, y, z) -c (k, l, m) = c (xk, yl, zm).

Łatwo zauważyć, że współrzędne po prostu trzeba dodać lub odjąć, w zależności od konkretnego zadania.

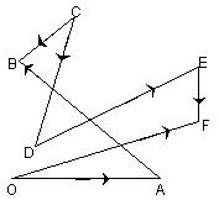
Pierwszy przykład z rozwiązaniem

Stan Biorąc pod uwagę prostokąt AVSD. Boki mają 6 i 8 cm, punkt przecięcia przekątnych jest oznaczony literą O. Wymagane jest obliczenie różnicy wektorów AO i VO.

Decyzja. Najpierw musisz narysować te wektory. Są one skierowane od wierzchołków prostokąta do punktu przecięcia przekątnych.

Jeśli przyjrzysz się dokładnie rysunkowi, zobaczysz, że wektory są już wyrównane, tak że drugi z nich jest w kontakcie z końcem pierwszego. To tylko jego kierunek jest zły. Musi zacząć od tego momentu. Jest tak, jeśli wektory są sumowane, a w problemie - odejmowanie. Zatrzymaj się To działanie oznacza, że ​​musisz dodać wektor skierowany przeciwnie. Oznacza to, że VO wymaga wymiany na OB. I okazuje się, że dwa wektory już utworzyły parę boków od reguły trójkąta. Dlatego wynikiem ich dodania, czyli pożądanej różnicy, jest wektor AB.

I pokrywa się z bokiem prostokąta. Aby zarejestrować odpowiedź numeryczną, wymagane będą następujące elementy. Narysuj prostokąt wzdłuż tak, aby duża strona biegła poziomo. Numeracja wierzchołków zaczyna się od lewego dolnego rogu i przechodzi w przeciwnym kierunku. Następnie długość wektora AB będzie równa 8 cm.

Odpowiedź jest. Różnica między AO i VO wynosi 8 cm.

Drugi przykład i jego szczegółowe rozwiązanie

Stan Przekątna AVSD rombu jest równa 12 i 16 cm, punkt ich przecięcia jest oznaczony literą O. Oblicz długość wektora utworzonego przez różnicę wektorów AO i VO.

Decyzja. Niech oznaczenie wierzchołków rombu będzie takie samo jak w poprzednim problemie. Podobnie jak w rozwiązaniu pierwszego przykładu, okazuje się, że pożądana różnica jest równa wektorowi AB. A jego długość jest nieznana. Rozwiązanie problemu zostało zredukowane do obliczenia jednej ze stron rombu.

W tym celu należy wziąć pod uwagę trójkąt ABO. Jest prostokątny, ponieważ przekątna rombu przecina się pod kątem 90 stopni. A jego nogi są równe połowie przekątnych. To znaczy, 6 i 8 cm. Strona poszukiwana w tym problemie pokrywa się z przeciwprostokątną w tym trójkącie.

Aby go znaleźć, potrzebujemy twierdzenia Pitagorasa. Kwadrat przeciwprostokątnej będzie równy sumie liczb 6 ² i 8 ² . Po kwadraturze wartości wynoszą 36 i 64. Ich suma wynosi 100. Z tego wynika, że ​​przeciwprostokątna wynosi 10 cm.

Odpowiedź jest. Różnica między wektorami AO i HE wynosi 10 cm.

Trzeci przykład ze szczegółowym rozwiązaniem

Stan Oblicz różnicę i sumę dwóch wektorów. Ich współrzędne są znane: w pierwszym - 1 i 2, w drugim - 4 i 8.

Decyzja. Aby znaleźć kwotę, musisz dodać w parach pierwszą i drugą współrzędną. Rezultatem będą liczby 5 i 10. Odpowiedzią będzie wektor o współrzędnych (5; 10).

Aby uzyskać różnicę, należy odjąć współrzędne. Po wykonaniu tej akcji otrzymasz liczby -3 i -6. Będą to współrzędne pożądanego wektora.

Odpowiedź jest. Suma wektorów wynosi (5; 10), ich różnica wynosi (-3; -6).

Czwarty przykład

Stan Długość wektora AB wynosi 6 cm, BC - 8 cm, druga grafika jest narysowana od końca pierwszego pod kątem 90 stopni. Oblicz: a) różnicę modułów wektorów BA i BC oraz moduł różnicy BA i BC; b) suma tych samych modułów i modułu sumy.

Rozwiązanie: a) Długości wektorów są już podane w problemie. Dlatego obliczenie ich różnicy nie jest trudne. 6 - 8 = -2. Sytuacja z modułem różnicowym jest nieco bardziej skomplikowana. Najpierw musisz wiedzieć, który wektor będzie wynikiem odejmowania. W tym celu należy odłożyć wektor BA, który jest skierowany w przeciwnym kierunku AB. Następnie od jego końca utrzymuj wektor słońca, kierując go w kierunku przeciwnym do oryginału. Wynikiem odejmowania jest wektor CA. Jego moduł można obliczyć za pomocą twierdzenia Pitagorasa. Proste obliczenia prowadzą do wartości 10 cm.

b) Suma modułów wektorów wynosi 14 cm. Aby znaleźć drugą odpowiedź, wymagana jest pewna konwersja. Wektor BA jest przeciwnie skierowany do tego podanego przez - AB. Oba wektory są skierowane z jednego punktu. W tej sytuacji możesz użyć reguły równoległoboku. Rezultatem dodania będzie przekątna, a nie tylko równoległobok, ale prostokąt. Jego przekątne są równe, co oznacza, że ​​moduł sumy jest taki sam jak w poprzednim paragrafie.

Odpowiedź: a) -2 i 10 cm; b) 14 i 10 cm.