Trygonometria od podstaw: podstawowe pojęcia, historia

Sinus, cosinus, stangens - wymawiając te słowa w obecności uczniów szkół średnich, możesz mieć pewność, że dwie trzecie z nich straci zainteresowanie dalszą rozmową. Przyczyna leży w tym, że podstawy trygonometrii w szkole są nauczane w całkowitej izolacji od rzeczywistości, a zatem uczniowie nie widzą sensu studiowania formuł i twierdzeń.

W rzeczywistości, po bliższym zbadaniu, ten obszar wiedzy okazuje się dość interesujący, a także stosowany - trygonometria znajduje zastosowanie w astronomii, budownictwie, fizyce, muzyce i wielu innych dziedzinach.

Zapoznajmy się z podstawowymi pojęciami, a podamy kilka powodów do studiowania tego działu nauk matematycznych.

Historia

Nie wiadomo, w którym momencie ludzkość zaczęła tworzyć od podstaw trygonometrię przyszłości. Udokumentowano jednak, że już w drugim tysiącleciu pne Egipcjanie znali podstawy tej nauki: archeolodzy znaleźli papirus z zadaniem, w którym konieczne jest znalezienie kąta nachylenia piramidy na dwóch znanych bokach.

Poważniejszy sukces osiągnęli naukowcy ze starożytnego Babilonu. Przez stulecia, zajmując się astronomią, opanowali wiele twierdzeń, wprowadzili specjalne sposoby mierzenia kątów, które, nawiasem mówiąc, używamy dzisiaj: stopnie, minuty i sekundy zostały zapożyczone przez europejską naukę w kulturze grecko-rzymskiej, w której jednostki te pochodziły z Babilonu.

Zakłada się, że słynne twierdzenie Pitagorasa, związane z podstawami trygonometrii, było znane Babilonomom prawie cztery tysiące lat temu.

Imię

Dosłownie, termin "trygonometria" można przetłumaczyć jako "trójkąty pomiarowe". Głównym przedmiotem badań w tej części nauki przez wiele stuleci trójkąt prostokątny lub raczej związek między wielkościami kątów i długościami ich boków (dzisiaj, badanie trygonometrii od zera zaczyna się od tej sekcji). W życiu występują często sytuacje, w których praktycznie niemożliwe jest zmierzenie wszystkich wymaganych parametrów obiektu (lub odległości od obiektu), a następnie uzyskanie danych za pomocą obliczeń staje się konieczne.

Na przykład w przeszłości osoba nie mogła zmierzyć odległości obiekty kosmiczne ale próby obliczenia odległości następują na długo przed nastaniem naszej ery. Trygonometria również odegrała ważną rolę w nawigacji: mając pewną wiedzę, kapitan mógł zawsze nawigować w nocy przez gwiazdy i dostosowywać kurs.

Podstawowe pojęcia

Aby opanować trygonometrię od zera, musisz zrozumieć i zapamiętać kilka podstawowych pojęć.

Sinus o pewnym kącie jest stosunkiem przeciwnej nogi do przeciwprostokątnej. Wyjaśniliśmy, że przeciwna noga jest stroną przeciwną do kąta, który rozważamy. Tak więc, jeśli kąt wynosi 30 stopni, sinus tego kąta będzie zawsze, dla dowolnego rozmiaru trójkąta, równy ½. Cosinus kąta jest stosunkiem sąsiedniej nogi do przeciwprostokątnej.

Styczna jest stosunkiem przeciwnej nogi do sąsiedniej (lub, równoważnie, stosunku sinusoidy do cosinusu). Cotangens to jednostka podzielona przez styczną.

Warto wspomnieć o słynnym Pi (3.14 ...), które stanowi połowę obwód o promieniu jednego urządzenia.

Popularne błędy

Ludzie, którzy studiują trygonometrię od podstaw, popełniają szereg błędów - głównie z powodu nieuwagi.

Po pierwsze, przy rozwiązywaniu problemów w geometrii należy pamiętać, że użycie sinusoidy i cosinusów jest możliwe tylko w trójkącie prostokątnym. Zdarza się, że uczeń "na maszynie" zajmuje najdłuższy bok trójkąta na przeciwprostokątnej i otrzymuje błędne wyniki obliczeń.

Po drugie, na początku łatwo jest pomylić wartości sinusa i cosinusa dla wybranego kąta: przypominamy, że sinus 30 stopni jest liczbowo równy cosinusowi 60 i odwrotnie. Przy zastępowaniu niewłaściwą liczbą wszystkie dalsze obliczenia będą błędne.

Po trzecie, dopóki problem nie zostanie całkowicie rozwiązany, nie należy zaokrąglać żadnych wartości, wyodrębnić pierwiastków, zapisać zwykłego ułamka jako dziesiętnego. Często uczniowie starają się uzyskać "piękną" liczbę w zadaniu trygonometrii i natychmiast wyodrębniają pierwiastek z trzech, chociaż w dokładnie jednej czynności ten pierwiastek może zostać zredukowany.

Etymologia słowa "sinus"

Historia słowa "zatokowy" jest naprawdę niezwykła. Faktem jest, że dosłowne tłumaczenie tego słowa z łaciny oznacza "pusty". Wynika to z tego, że podczas tłumaczenia z jednego języka na inny poprawne zrozumienie tego słowa zostało utracone.

Nazwy podstawowych funkcji trygonometrycznych pochodziły z Indii, gdzie pojęcie sinusa oznaczono słowem "cięciwa łuku" w sanskrycie - faktem jest, że segment wraz z łukiem koła, na którym się on opierał, przypominał łuk. Podczas rozkwitu cywilizacji arabskiej zapożyczono hinduskie osiągnięcia w dziedzinie trygonometrii, a termin został przeniesiony na język arabski w formie transkrypcji. Tak się złożyło, że w tym języku istniało już podobne słowo oznaczające zagłębienie, a jeśli Arabowie zrozumieli fonetyczną różnicę między słowem rodzimym a zapożyczonym, to Europejczycy, którzy przetłumaczyli naukowe połacie na łacinę dosłownie przetłumaczyli arabskie słowo, bez związku z pojęciem zatoki . Używamy ich do dziś.

Tabele wartości

Są tabele, w których wprowadzane są wartości liczbowe dla sinusów, cosinusów i stycznych wszystkich możliwych kątów. Poniżej przedstawiamy dane dla kątów 0, 30, 45, 60 i 90 stopni, których należy się nauczyć jako obowiązkowej sekcji trygonometrii dla manekinów, korzyść z zapamiętania ich jest dość łatwa.

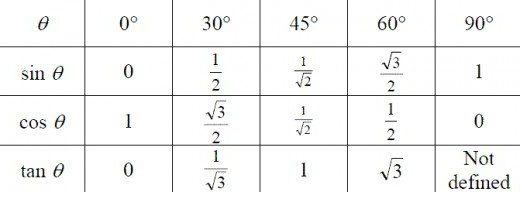Jeśli zdarza się, że wartość liczbowa sinusa lub cosinusa kąta "wyleciała z głowy", istnieje sposób na samodzielne wyprowadzenie go.

Reprezentacja geometryczna

Narysuj okrąg, przez jego środek narysujemy oś odciętych i osi rzędnych. Oś odciętych znajduje się w poziomie, oś rzędnych jest pionowa. Zwykle są one podpisane odpowiednio jako "X" i "Y". Teraz od środka okręgu narysujemy linię w taki sposób, aby uzyskać kąt potrzebny między nią a osią X. Wreszcie, od punktu, w którym linia prosta przecina okrąg, obniżamy prostopadle do osi X. Długość wynikowego segmentu będzie równa wartości liczbowej sinusa naszego kąta.

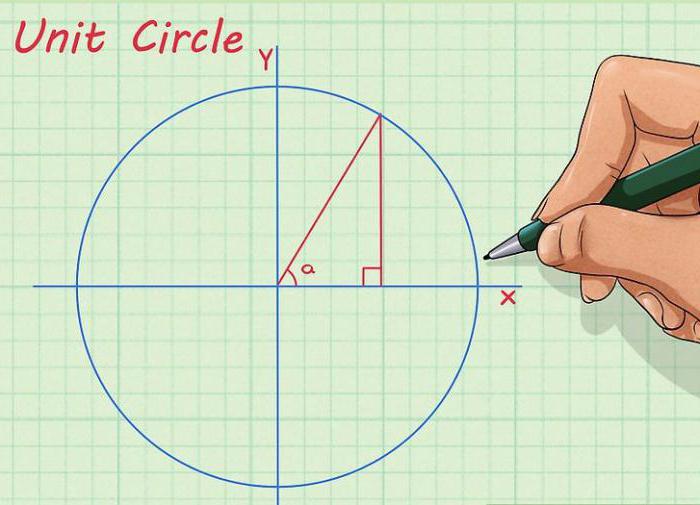Ta metoda jest bardzo istotna, jeśli zapomniałeś o pożądanej wartości, na przykład na egzaminie i nie ma podręcznika dotyczącego trygonometrii. W ten sposób nie uzyskasz dokładnej liczby, ale na pewno zobaczysz różnicę między ½ a 1,73 / 2 (sinus i cosinus z kątem 30 stopni).

Aplikacja

Jednym z pierwszych specjalistów używających trygonometrii byli żeglarze, którzy nie mieli żadnego innego punktu odniesienia na otwartym morzu, z wyjątkiem nieba nad ich głowami. Dziś kapitanowie statków (samoloty i inne rodzaje transportu) Nie szukają najkrótszej ścieżki przez gwiazdy, ale aktywnie uciekają się do nawigacji GPS, co byłoby niemożliwe bez użycia trygonometrii.

W prawie każdym sekcja fizyki Czekasz na obliczenia za pomocą sinusoidy i cosinusów: czy to jest zastosowanie siły w mechanice, obliczenia ścieżki obiektów w kinematyce, oscylacje, propagacja fal, załamanie światła - po prostu nie da się obejść bez podstawowej trygonometrii w formułach.

Innym zawodem, który jest nie do pomyślenia bez trygonometrii, jest geodeta. Używając teodolitu i poziomu lub bardziej złożonego urządzenia - tachyometru, ludzie ci mierzą różnicę wysokości między różnymi punktami na powierzchni Ziemi.

Powtarzalność

Trygonometria zajmuje się nie tylko kątami i bokami trójkąta, ale od tego momentu zaczęła swoją egzystencję. We wszystkich obszarach, w których występuje cykliczność (biologia, medycyna, fizyka, muzyka itp.), Napotkasz harmonogram, którego nazwę prawdopodobnie znasz jako falę sinusoidalną.

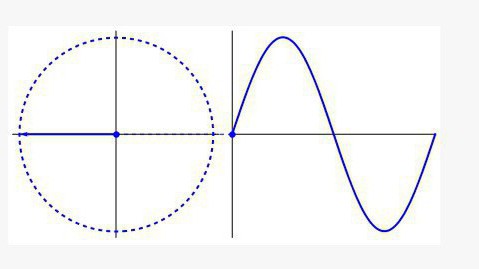Taki wykres jest kołem ułożonym wzdłuż osi czasu i wygląda jak fala. Jeśli kiedykolwiek pracowałeś z oscyloskopem w klasie z fizyki, rozumiesz o co chodzi. Zarówno korektor muzyczny, jak i urządzenie wyświetlające rytmy serca wykorzystują w swojej pracy trygonometryczne formuły.

Podsumowując

Myśląc o tym, jak nauczyć się trygonometrii, większość uczniów szkół średnich i średnich zaczyna uważać to za skomplikowaną i niepraktyczną naukę, ponieważ poznają tylko nudne informacje z podręcznika.

W odniesieniu do niepraktyczności - już widzieliśmy, że w różnym stopniu, zdolność do obsługi sinusoidy i stycznych jest wymagana w prawie każdej dziedzinie działalności. Co do złożoności ... Pomyśl: gdyby ludzie korzystali z tej wiedzy ponad dwa tysiące lat temu, kiedy dorosły miał mniej wiedzy niż dzisiejszy uczeń szkoły średniej, to czy naprawdę można studiować tę dziedzinę nauki na poziomie podstawowym? Kilka godzin przemyślanych lekcji z rozwiązywaniem problemów - i osiągniesz swój cel, studiując podstawowy kurs, tak zwaną trygonometrię dla manekinów.