Maszyna Turinga: opis i przykłady maszyn Turinga
Maszyna Turinga jest jednym z najbardziej intrygujących i ekscytujących odkryć intelektualnych XX wieku. Jest to prosty i użyteczny abstrakcyjny model komputerowy (komputerowy i cyfrowy), który jest dość powszechny w realizacji dowolnego zadania komputerowego. Dzięki prostemu opisowi i zachowaniu analiza matematyczna stanowi podstawę teoretycznej informatyki. Badanie to doprowadziło do pogłębienia wiedzy na temat komputerów cyfrowych i rachunku różniczkowego, w tym zrozumienia, że istnieją pewne problemy obliczeniowe, których nie można rozwiązać na zwykłych komputerach użytkowników. 
Co to jest i kto stworzył
Alan Turing próbował opisać najbardziej prymitywny model urządzenia mechanicznego, który miałby takie same podstawowe możliwości jak komputer. Turing po raz pierwszy opisał samochód w 1936 roku w artykule "O liczbach obliczalnych z zastosowaniem do problemu rozwiązalności", który pojawił się w Proceedings of London Mathematical Society. 
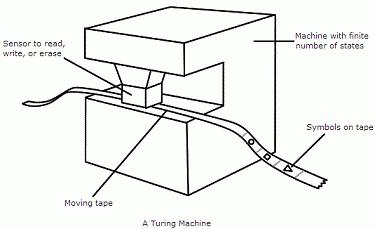
Maszyna Turinga to urządzenie komputerowe składające się z głowicy odczytu / zapisu (lub "skanera") z przechodzącą przez nią taśmą papierową. Taśma podzielona jest na kwadraty, z których każdy przenosi pojedynczy znak - "0" lub "1". Celem mechanizmu jest to, że działa on zarówno jako środek do wejścia i wyjścia, jak i jako pamięć robocza do przechowywania wyników pośrednich etapów obliczeń.
Z czego składa się urządzenie
Każda taka maszyna składa się z dwóch komponentów:
- Nieograniczona taśma. Jest nieskończony w obu kierunkach i podzielony na komórki.
- Automatycznie kontrolowany program, głowica skanera do odczytu i zapisu danych. Może być w każdej chwili w jednym z wielu stanów.
Każda maszyna łączy dwie skończone serie danych: alfabet przychodzących symboli A = {a0, a1, ..., am} i alfabet stanów Q = {q0, q1, ..., qp}. Stan q0 nazywany jest pasywnym. Uważa się, że urządzenie kończy swoją pracę, gdy spada na niego. Stan q1 nazywany jest początkowym - maszyna rozpoczyna obliczenia, będąc na początku w nim. Słowo wejściowe znajduje się na taśmie jedna litera z rzędu w każdej pozycji. Po obu stronach są tylko puste komórki.
Jak działa ten mechanizm
Maszyna Turinga ma fundamentalną różnicę od urządzeń komputerowych - jej pamięć ma nieskończoną taśmę, podczas gdy w przypadku urządzeń cyfrowych to urządzenie ma pasek o określonej długości. Każda klasa zadań jest rozwiązywana tylko przez jedną zbudowaną maszynę Turinga. Inne typy zadań obejmują pisanie nowego algorytmu.
Urządzenie sterujące, będąc w jednym stanie, może poruszać się w dowolnym kierunku wzdłuż pasa. Piszą do komórek i odczytują z nich znaki ostatniego alfabetu. W procesie przenoszenia wybrany jest pusty element, który wypełnia pozycje, które nie zawierają danych wejściowych. Algorytm maszyny Turinga określa zasady przejścia dla urządzenia sterującego. Ustawiają głowicę do odczytu i zapisu na następujące parametry: zapis do komórki nowej postaci, przejście do nowego stanu, przesuwanie w lewo lub w prawo wzdłuż taśmy. 
Właściwości mechanizmu
Maszyna Turinga, podobnie jak inne systemy komputerowe, ma swoje nieodłączne cechy i są one podobne do właściwości algorytmów:
- Dyskrecja Maszyna cyfrowa przechodzi do następnego etapu n + 1 dopiero po zakończeniu poprzedniej. Każdy ukończony krok przypisuje wartość n + 1.
- Zrozumiałość Urządzenie wykonuje tylko jedną akcję dla tej samej komórki. Wstawia znak z alfabetu i wykonuje jeden ruch: w lewo lub w prawo.
- Determinizm. Każda pozycja w mechanizmie odpowiada jednemu przykładowi wykonania określonego schematu, a na każdym etapie działania sekwencja ich wykonania jest jednoznaczna.
- Wydajność. Dokładny wynik dla każdego etapu jest określony przez maszynę Turinga. Program wykonuje algorytm iw skończonej liczbie kroków przechodzi do stanu q0.
- Msza św. Każde urządzenie jest zdefiniowane powyżej prawidłowych słów w alfabecie.
Funkcje maszyny Turinga
Rozwiązanie algorytmów często wymaga implementacji funkcji. W zależności od możliwości napisania łańcucha do obliczeń, funkcja nazywa się algorytmicznie rozwiązywaną lub nierozpuszczalną. Jako zbiór liczb naturalnych lub wymiernych, słów w skończonym alfabecie N dla maszyny, rozpatrywana jest sekwencja zbioru B - słowa w alfabecie kodu binarnego B = {0,1}. Wynik obliczenia uwzględnia również wartość "niezdefiniowaną", która występuje, gdy zawiesza się algorytm. W celu realizacji funkcji ważne jest posiadanie sformalizowanego języka w ostatecznym alfabecie i rozwiązywanie problemu rozpoznawania poprawnych opisów. 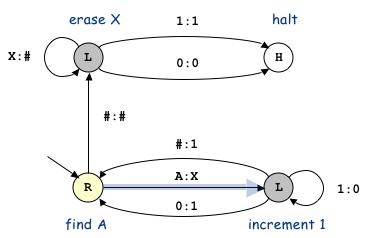
Program dla urządzenia
Programy dla mechanizmu Turinga są tworzone przez tabele, w których pierwszy wiersz i kolumna zawierają znaki alfabetu zewnętrznego i wartości możliwych stanów wewnętrznych automatu - wewnętrznego alfabetu. Dane tabelaryczne są poleceniami, które są postrzegane przez maszynę Turinga. Rozwiązanie problemów występuje w ten sposób: litera odczytana przez głowę w komórce, nad którą obecnie się znajduje, a stan wewnętrzny głowy automatu określa, które polecenie powinno zostać wykonane. W szczególności takie polecenie znajduje się na przecięciu symboli alfabetu zewnętrznego i wewnętrznego, które znajdują się w tabeli. 
Komponenty do obliczeń
Aby zbudować maszynę Turinga do rozwiązania jednego określonego zadania, konieczne jest określenie dla niego następujących parametrów.
Zewnętrzny alfabet. Jest to pewien skończony zestaw symboli, oznaczony przez znak A, którego elementy składowe nazywane są literami. Jeden z nich - a0 - musi być pusty. Na przykład alfabet urządzenia Turinga pracującego z liczbami binarnymi wygląda następująco: A = {0, 1, a0}.
Ciąg ciąg znaków alfanumerycznych zapisanych na taśmie nazywany jest słowem.
Automat to urządzenie, które działa bez interwencji człowieka. W maszynie Turinga ma kilka różnych stanów rozwiązywania problemów i, pod pewnymi warunkami, przemieszcza się z jednej pozycji do drugiej. Połączenie takich stanów przewozu jest alfabetem wewnętrznym. Ma oznaczenie literowe postaci Q = {q1, q2 ...}. Jedno z tych postanowień - q1 - powinno być początkowe, czyli to, co uruchamia program. Kolejnym niezbędnym elementem jest stan q0, który jest skończony, czyli kończy program i umieszcza urządzenie w pozycji zatrzymania.
Tabela konwersji. Ten komponent jest algorytmem zachowania karetki urządzenia, w zależności od tego, jaki jest obecnie stan maszyny i wartość odczytanego symbolu. 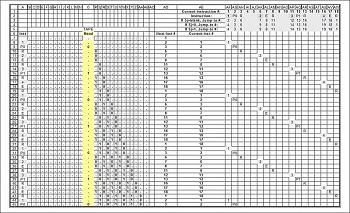
Algorytm automatyczny
Wózek urządzenia Turinga podczas pracy jest sterowany przez program, który podczas każdego kroku wykonuje sekwencję następujących czynności:
- Zapisywanie zewnętrznego alfabetu w pozycji, w tym pustej, poprzez zastąpienie elementu, który się w niej znajdował, w tym pustego.
- Przesuń o jeden krok w lewo lub w prawo.
- Zmień swój stan wewnętrzny.
Dlatego przy pisaniu programów dla każdej pary znaków lub pozycji należy dokładnie opisać trzy parametry: a - element z wybranego alfabetu A, kierunek przesunięcia karetki ("←" w lewo, "→" w prawo, "punkt" - brak ruchu) i q k jest nowym stanem urządzenia, np. polecenie 1 "←" q 2 jest ustawione na "zastąpienie znaku o 1, przesunięcie głowicy karetki w lewo o jedną komórkę schodkową i przejście do stanu q 2 ".
Maszyna Turinga: przykłady
Przykład 1. Biorąc pod uwagę zadanie zbudowania algorytmu, który dodaje jeden do ostatniej cyfry danej liczby znajdującej się na taśmie. Dane wejściowe - słowo - cyfry całej liczby dziesiętnej, zapisane w kolejnych komórkach na taśmie. W początkowej chwili urządzenie znajduje się naprzeciwko prawostronnego symbolu - cyfry numeru.
Decyzja. Jeśli ostatnia cyfra jest równa 9, to musi zostać zastąpiona przez 0, a następnie dodać jedną do poprzedzającego znaku. Program w tym przypadku dla tego urządzenia Turinga można napisać tak:
| a 0 | 0 | 1 | 2 | 3 | ... | 7 | 8 | 9 | |
| q 1 | 1 H q 0 | 1 H q 0 | 2 H q 0 | 3 H q 0 | 4 H q 0 | ... | 8 H q 0 | 9 H q 0 | 0 λ q 1 |
Tutaj q 1 jest stanem zmiany cyfry, q 0 jest stopem. Jeśli w q 1 automat naprawi element z serii 0..8, to zastąpi go odpowiednio jednym z 1..9, a następnie przełączy się w stan q 0 , czyli urządzenie zatrzyma się. Jeśli karetka ustali liczbę 9, zastępuje ją 0, następnie przesuwa się w lewo, zatrzymując się w stanie q 1 . Ten ruch trwa, dopóki urządzenie nie ustali cyfry mniejszej niż 9. Jeśli wszystkie znaki są równe 9, zostaną zastąpione zerami, 0 zostanie zastąpione elementem wiodącym, karetka przesunie się w lewo i zapisze 1 w pustej komórce. Następnym krokiem będzie przejście do stanu q 0 - stop.
Przykład 2. Biorąc pod uwagę szereg znaków oznaczających nawiasy otwierające i zamykające. Wymagane jest zbudowanie urządzenia Turinga, które usunie parę nawiasów wzajemnych, czyli elementów ułożonych w rzędzie - "()". Na przykład początkowe dane: ") (() (()", odpowiedź powinna brzmieć: ") .. ((. Rozwiązanie: mechanizm, będąc w q 1 , analizuje lewy element w linii.
| a 0 | ( | ) | |
| q 1 | a 0 H q 0 | (P q 2 | ) P q 1 |
| q 2 | a 0 H q 0 | (P q 2 | ) λ q 3 |
| q 3 | a 0 H q 0 | a 0 n q 3 | a 0 n q1 |
Stan q 1 : jeśli napotkany zostanie symbol "(", przesuń w prawo i przejdź do pozycji q 2 , jeśli "a 0 " jest zdefiniowane, zatrzymaj się.
Stan q 2 : analiza nawiasów "(" w przypadku obecności pary jest wykonywana, w przypadku zbiegów okoliczności powinna się okazać ")" Jeśli element jest parą, wykonaj powrót karetki w lewo i przejdź do q 3 .
Stan q 3 : najpierw usuń symbol "(", a następnie ")" i przejdź do q 1 .