Co to jest stożek w geometrii? Definicja, formuły, problem z próbką
Znajomość właściwości figur geometrycznych pozwala nie tylko rozwiązywać problemy teoretyczne, ale także wykonywać różne, praktycznie ważne obliczenia. Jedną z takich postaci, których właściwości zostaną omówione w tym artykule, jest stożek. Czym jest stożek, jakie są jego rodzaje, jak znaleźć jego powierzchnię i objętość? Wszystkie te pytania są szczegółowo opisane poniżej.
Ogólna definicja stożka w geometrii
Stereometria, która bada charakterystyki figur w przestrzeni trójwymiarowej, oferuje następującą odpowiedź na pytanie, czym jest stożek: jest to figura, której powierzchnia jest utworzona przez zestaw odcinków prostych łączących pewien punkt w przestrzeni z pewną krzywą w płaszczyźnie.
Zaznaczony punkt przestrzeni nazywany jest wierzchołkiem stożka, proste odcinki są generacjami figury lub jej generatorów, a sama krzywa na płaszczyźnie jest kierunkiem.
Zgodnie z powyższą definicją nadaje się cała klasa figur, z których najbardziej znanymi są okrągłe, eliptyczne, paraboliczne i hiperboliczne. Liczbę eliptyczną przedstawiono poniżej.
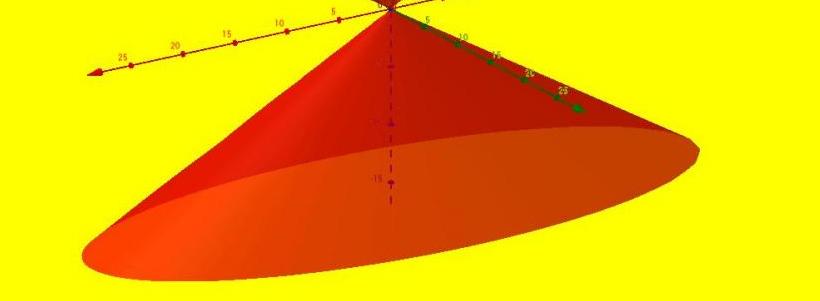
Kierownica tego stożka jest zamkniętą elipsą, która ogranicza podstawę figury. Generatory wszystkich stożków razem tworzą stożkową powierzchnię, która nazywa się boczną. Te dwie powierzchnie (podstawa i bok) ograniczają przestrzenną objętość, która jest zwykle nazywana objętością stożka.
Okrągły prosty stożek - liczba obrotów
Stożek eliptyczny pokazany na powyższym rysunku nie może zostać uzyskany w wyniku obrotu płaskiej figury. Jedynym przedstawicielem klasy stożków, która może być utworzona przez obrót, jest okrągły stożek prosty. Ta liczba jest pokazana poniżej.
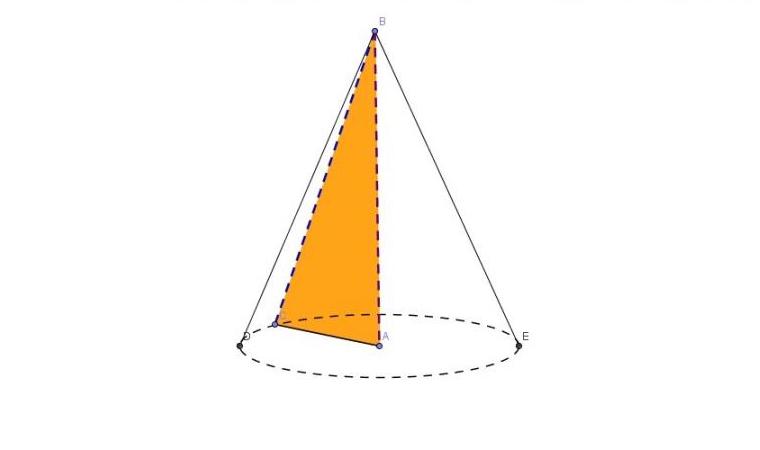
Widać, że jego podstawa reprezentuje idealny krąg. Ponadto, dowolny odcinek powierzchni bocznej z płaszczyzną równoległą do podstawy będzie również okręgiem, ale o mniejszej średnicy niż figura u podstawy.
Pomarańczowy trójkąt ABC, wybrany wewnątrz stożka, jest prostokątny. Widać, że jego noga AC jest promieniem podstawowym r. Noga AB to wysokość cyfry h. Zgodnie z konstrukcją jest oczywiste, że wysokość jest długością prostopadłości rozciągniętej od wierzchołka figury B do płaszczyzny podstawy (koła). Ta wysokość przecina okrąg w jego środku. To ostatnie oznacza, że stożek jest prosty. Wreszcie, przeciwprostokątna trójkąta BC jest niczym więcej niż stożkiem tworzącym.
Aby utworzyć stożek za pomocą opisanego trójkąta, należy go obrócić wokół boku AB.
Dla wizualnej reprezentacji różnicy między stożkami prostymi i ukośnymi przedstawiamy odpowiednią figurę.
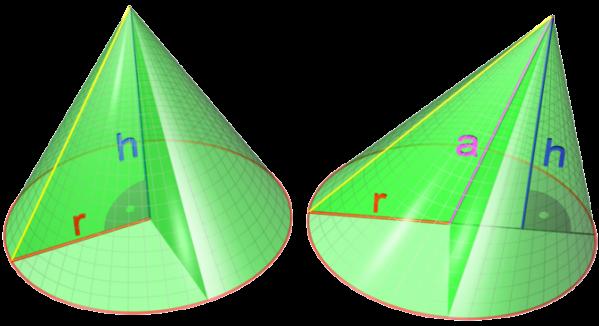
Różnica między tymi dwoma liczbami jest oczywista: jeśli ich podstawy są takie same, to wysokości obniżone od góry krzyżują podstawy w różnych punktach. Pierwsza figura jest prosta, druga jest ukośna.
Parametry liniowe okrągłego prostego stożka i kąta u podstawy
Parametry te zostały już wskazane powyżej. Wymień je ponownie:
- promień r;
- wysokość h;
- generatrix g.
Aby jednoznacznie zdefiniować stożek, te trzy parametry są zbędne, to znaczy, że daną figurę można skonstruować, a wszystkie jej właściwości można obliczyć, znając tylko dwa z trzech nazwanych parametrów. Opierając się na rozważanym schemacie dla uzyskania stożka obracając trójkąt prostokątny, możemy napisać następującą zależność między generatorem, promieniem i wysokością stożka:
g = √ (r² + h²).
Ta równość jest oczywista i nie wymaga dowodu (pamiętaj o twierdzeniu Pitagorasa).
Stożek można ustawiać nie tylko za pomocą odcinków prostych r, h i g, ale także za pomocą miary kątowej między dowolnym generatorem kształtu a płaszczyzną podstawy. Oznacz ten kąt literą φ. Korzystając z definicji funkcji trygonometrycznych, możemy napisać serię formuł, w których kąt φ łączy parametry liniowe. Piszemy te główne:
g = h / sin (φ);
g = r / cos (φ);
h = r * tg (φ).
Pole powierzchni figury
Biorąc pod uwagę kwestię tego, czym jest stożek, przedstawiamy wzór w celu określenia obszaru jego pełnej powierzchni. Aby wyjaśnić, co zostanie omówione, sprowadzimy skan do płaszczyzny figurki.
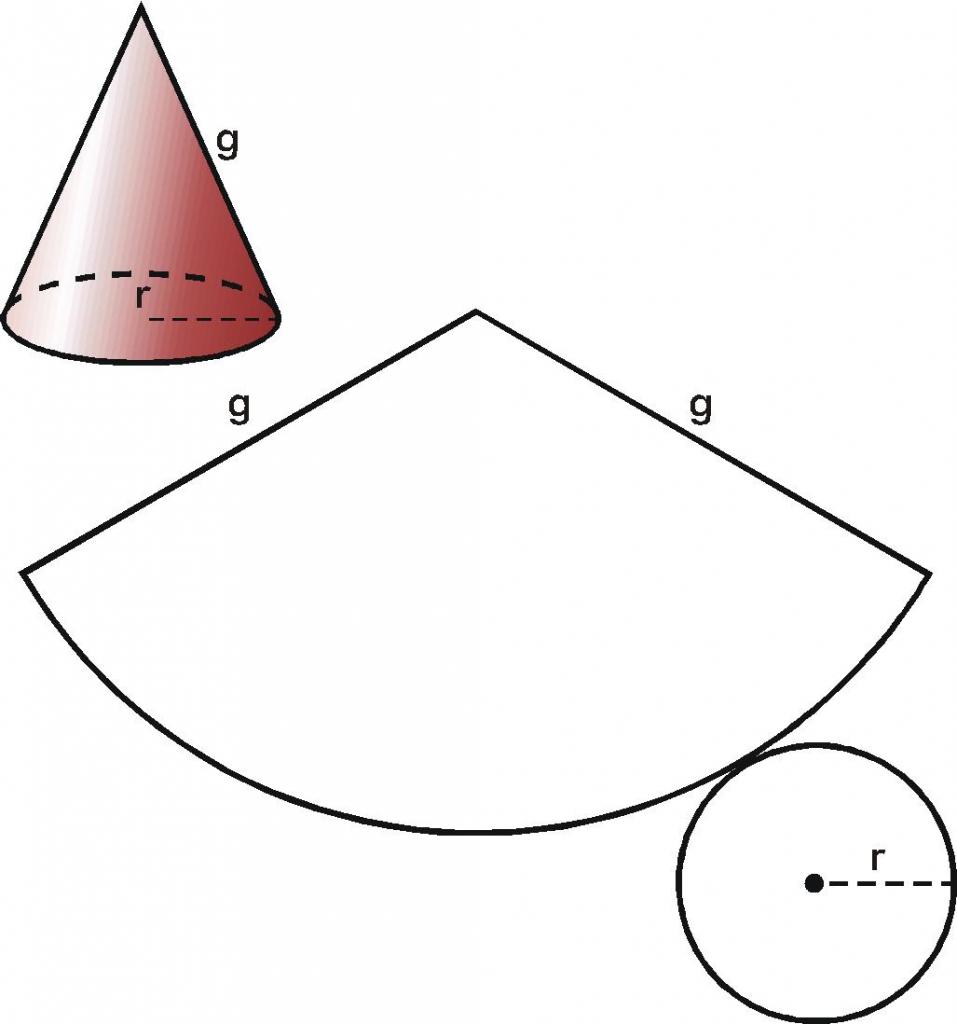
Rozwój stożka w samolocie składa się z dwóch postaci. Koło jest podstawą stożka, okrągły odcinek o promieniu g jest powierzchnią boczną. Okrągły sektor jest łatwy do zdobycia, jeśli weźmiesz papierową powierzchnię stożkową i pokroisz ją wzdłuż dowolnej tworzącej g. Rozszerzając tę powierzchnię, otrzymujemy żądany sektor.
Określenie obszaru S o koło nie stanowi problemu. Odpowiednie wyrażenie jest pokazane poniżej:
S o = pi * r².
Jeśli chodzi o sektor kołowy, znane są również jego niezbędne parametry do obliczania powierzchni Sb: promień g i długość łuku odpowiadająca obwodowi okręgu rozważanemu powyżej. Wzór do obliczenia powierzchni bocznej powierzchni stożka Sb wynosi:
S b = pi * r * g.
Zatem całkowita powierzchnia figury jest równa:
S = S o + S b = pi * r * (r + g).
Wzór na objętość

Wiedząc, co stożek jest prosty, łatwo jest zapisać wzór na jego objętość. Ponieważ figurę można uznać za piramidę o nieskończonej liczbie krawędzi bocznych, to dla niej, podobnie jak w przypadku każdej piramidy, objętość można obliczyć według wzoru:
V = 1/3 * S o * h.
Wartość kwadratu S o podaliśmy powyżej, dlatego wymagana formuła dla objętości stożka prostego z okrągłą podstawą będzie następująca:
V = 1/3 * pi * r² * godz.
Rozwiązywanie problemu geometrycznego
Wiadomo, że wartość pola powierzchni stożka okrągłej prostej wynosi 300 cm². Konieczne jest określenie promienia stożka, wiedząc, że jego tworząca jest 15 cm.
Piszemy równość dla obszaru i podstawiamy wartość g = 15 cm, a S = 300 cm², otrzymujemy:
S = pi * r * (r + g) =>
300 = pi * r² + 15 * pi * r.
Podziel lewą i prawą stronę przez liczbę pi, otrzymamy następujące równanie kwadratowe:
r ² + 15 * r - 95,54 = 0.
Rozwiążemy to równanie przez dyskryminatora, otrzymujemy:
D = 15² - 4 * (- 95,54) = 607,16;
r = (-15 ± √D) / 2 = (4,82; -19,82).
Ujemny root nie pasuje do stanu problemu, więc możesz napisać odpowiedź: dany stożek ma promień 4,82 cm.