Czym jest geometria? Definicja, cechy i gatunki

Czym jest geometria? Jest to nauka, która bada formy, relacje przestrzenne. Część matematyki poświęcona postaciom i ich wzajemnemu porozumieniu ma długą historię. Nauka pojawiła się w starożytności. Założyciel - matematyk Euclid.

Pierwsza informacja

Czym jest geometria? To jest nauka, która jest uważana za miejsce narodzin Egiptu. Początkowo była zwykłą jednostką geodezyjną. Grecy przekształcili otrzymaną informację od Egipcjan w ścisłą dyscyplinę. W starożytności to, co jest geometrią, znane jest również w Indiach, Chinach, Asyrii.

W czasach starożytnych nauka o tej nauce była spowodowana potrzebą mierzenia ziemi. Ponadto pierwsze istotne zmiany wymagały wyrównania, utrzymania pionu, uniewinnienia z planem i perspektywy. Konieczność pomiaru przedziałów czasowych wymagała systematycznej obserwacji ruchu opraw, a w konsekwencji pomiaru kątów. Czym jest geometria? To jest nauka, która pozwoliła starożytnym ludziom budować ogromne budynki. Niektóre z nich przetrwały do ​​dziś.

Tales of Miletus

Geometria to nauka, której pojawienie się greccy autorzy kojarzyli właśnie z tym imieniem. Aktywność Tales of Miletus została przedstawiona przez Hellenes w świetle słonecznym. Wiadomo, że w młodości podróżował po Egipcie, komunikował się z egipskimi kapłanami i uczył się od nich o geometrii. Ta nauka jest bardzo zainteresowana Tales. Po powrocie do wioski osiadł w Milecie, poświęcając się badaniu. Później założył szkołę jońską.

Co należy wiedzieć podczas pracy nad projektem "Geometria wokół nas"? Przede wszystkim o przyczynach, dla których ta nauka w czasach starożytnych rozwijała się bardzo szybko. Ważne jest oczywiście poznanie znaczenia słowa "geometria". Pomimo faktu, że fundamenty zostały złożone przez Egipcjan, sama nazwa dyscypliny pochodzi z greckiego. Przetłumaczone na język rosyjski, oznacza "zmierzyć ziemię".

Pod względem szybko rozwijającej się architektury, inżynierii lądowej, technologii cywilnej i wojskowej, skąpy materiał uzyskany od Egipcjan, Grecy, oczywiście, nie zadowalał. Podstawowe metody bezpośredniej obserwacji były bezsilne wobec nowych zadań.

Szkoła Jońska sprowadziła naukę Egipcjan do regionu z szeroką gamą pomysłów i zadań. Dała teoretyczny charakter geometrii. Powyższa definicja wkrótce przestała odpowiadać pierwotnym zadaniom.

Euclid

Około IV c. do n. e. zaczęły pojawiać się pierwsze prace. Na przykład "Start". W tej pracy Euklides usystematyzował całą wiedzę zdobytą w tym czasie.

Ο Życie tego naukowca jest również prawie nieznane. Przed nami były tylko legendy o nim. Pierwszy komentator programu "Początek", który żył w V wieku naszej ery, nie mógł nawet wskazać, gdzie Euclid urodził się i zmarł.

Jedna z legend głosi, że król Ptolemeusz postanowił kiedyś studiować geometrię. Okazało się jednak, że nie jest to łatwe. Potem zadzwonił do Euklidesa i poprosił go, aby dał mu łatwą drogę. "Nie ma królewskiej drogi do geometrii" - powiedział naukowiec. Tak więc w formie legendy, daj nam wyraz, który został uskrzydlony.

W Aleksandrii Euclid założył szkołę matematyczną i napisał wspaniałe dzieło na temat geometrii - "Początek". Twierdzi się, że zostało napisane około 325 lat przed naszą erą.

"Początek"

Zarówno moderniści, jak i badacze euklidesowi byli przyciągani przez systematyczne i logiczne informacje. "The Beginnings" składa się z trzynastu książek, zbudowanych w ramach jednego logicznego schematu. Każda z książek zaczyna się od zidentyfikowania napięć (linii, linii, wysokości, sylwetki itp.), Które są w nim używane, a następnie na niewielkiej liczbie podstawowych ćwiczeń (pięć osi i ten sam nieformowany). geometria.

W starożytności rozwój nauki nie sugerował istnienia metod matematyki praktycznej. Pierwsze cztery książki obejmowały geometrię, ich treść została napisana przez pitagorejskie szkoły. W części piątej opracowano doktrynę organizacji, która przylegała do Eudox Ciddes. W piątej do dziewiątej księgi było nauczanie liczb, reprezentujące rozwój podstawowych źródeł pitagorejskich. Następujące części będą zawierać rozmieszczenie obszarów w przestrzeni i przestrzeni (stereometria), teorię irracjonalności. W finale umieszczane są badania właściwych ciał.

"Początki" Euclida są przedstawieniem tej nauki, która jest nadal znana pod nazwą "geometria euklidesowa". Jako założenia autor wybrał twierdzenia, które można zweryfikować za pomocą najprostszych asercji za pomocą kompasu i linijki. Euklides zaakceptował także pewne ogólne aksjomaty ofert. Na przykład dwie wielkości, równe trzeciej, są między sobą równe. Na podstawie takich konstrukcji i aksjomatu Euklides ściśle i systematycznie opracował całą planimetrię.

Archimedes

Naukowiec posiada wzór do wyznaczania obszaru trójkąta przez trzy jego partie (błędnie nazywane formułą Herona). Starożytny grecki matematyk przedstawił (nie wyczerpującą) teorię poprawnych wypukłych wielokątów (ciała Archimedesa). Aksjomat "Archimedesa" ma szczególne znaczenie: od nierównej ostrości mniejsza liczba będzie większa niż w nierównych odległościach. Ten aksjomat określa tak zwany porządek Archimedesa, który odgrywa ważną rolę we współczesnej matematyce. Starożytny grecki matematyk napisał numer, który zapisał i nazwał bardzo dużą liczbę. Z wielką precyzją wyznaczył wartość liczby i wskazał granice grzechu.

Kartezjusz

Upadek starożytnego społeczeństwa doprowadził do względnego zastoju w rozwoju geometrii. Jednak rozwija się w Indiach, w Azji Środkowej, w krajach arabskiego Wschodu. Nadejście nauki i sztuki w Europie przyciągnęło dalszy rozkwit geometrii. W nauce w pierwszej części XVII wieku dokonał się zupełnie nowy krok R. Descartes, który wprowadził metodę współrzędnych, która pozwala nam powiązać naukę z opracowaną algebrą i powstającą analizą.

Zastosowanie metod tych dyscyplin dało początek innym rodzajom geometrii: analitycznej, a więc różnej. Nauka przeniosła się na jakościowo nowy poziom. Zajmuje się już bardziej ogólnymi danymi i stosuje zasadniczo nowe metody.

Widoki

Geometria analityczna bada liczby i przekształcenia podane równaniami algebraicznymi w bezpośrednich współrzędnych, używając metod algebry. Różnica, powstała w XVIII wieku, odkrywa już całkiem gładkie zakrzywione linie i powierzchnie, ich rodziny i przekształcenia. Jego nazwa jest związana z metodą wyprowadzoną z rachunku różniczkowego.

XVII-XIX wiek

W pierwszej ćwierci XVII w. Zainicjowano powstawanie geometrii rzutowej w twórczości J. Dezarguesa i B. Pascala. Wyłonił się z problemu wizerunku ciał na stronie. Jej pierwszym celem są dzieła sztuki, które zachowały się, gdy projektowane są z jednego miejsca z dowolnego miejsca.

Pierwotne kształtowanie i systematyczne przedstawianie tych nowych kierunków geometrii zostało przedstawione na początku XIX w. Przez Eulera dla analizy, dla dyferencjału, J. Fonsela dla geometrii rzutowej. A nauka samego obrazu (w bezpośrednim związku z zadaniami rysowania) została opracowana jeszcze wcześniej i wprowadzona do systemu przez Moneza w formie geometrii opisowej. We wszystkich tych nowych dyscyplinach zasady (aksjomaty, oryginalne pojęcia) nauki pozostały niezmienione. Rozszerzono zakres badanych postaci i ich właściwości, a także stosowanych metod.

Łobaczewski

W rozwoju nauki w XIX wieku rozpoczyna się nowy etap. Była geometria nieeuklidesowa (lub Łobaczewski). Niezależny od rosyjskiego matematyka w 1832 roku ten sam punkt widzenia został sformułowany przez J. Bolyai. Łobaczewski uważał swoją geometrię za potencjalną teorię stosunków przestrzennych. Było to jednak hipotetyczne, chociaż jego prawdziwe znaczenie nie zostało wyjaśnione, a zatem podano pełne uzasadnienie.

Rewolucja w geometrii, wyprodukowana przez Łobaczewskiego, w jej wartości nie ustępuje żadnemu z nawróceń w historii naturalnej. Nie jest zbiegiem okoliczności, że został nazwany "geometrią Couriera". W jego idei zarysowano trzy zasady, które determinowały nowy rozwój tej dyscypliny.

Po pierwsze, nie tylko geometria euklidesowa jest logicznie do pomyślenia, ale także inne gałęzie nauki. Druga zasada opiera się na konstrukcji nowych teorii, modyfikując i syntetyzując podstawowe pojęcia sformułowane przez starożytnego greckiego matematyka. Trzeci polega na tym, że prawdę teorii geometrycznej, w sensie zgodności z rzeczywistymi właściwościami przestrzeni, można zweryfikować tylko fizycznymi badaniami, i możliwe jest, że w ten sposób ustalą niedokładność geologii euklidesowej. Potwierdziła to nowoczesna fizyka.

Ponadto nie traci się matematycznej dokładności geometrii euklidesowej. Określa ją logika (brak ciągłości) teorii starożytnego greckiego uczonego. Podobnie, w związku z jakąkolwiek teorią geometryczną, konieczne jest rozróżnienie ich prawdy fizycznej i matematycznej. Pierwszy test weryfikacyjny jest zgodny z prawem. W drugim - w logistycznej niepołączalności.

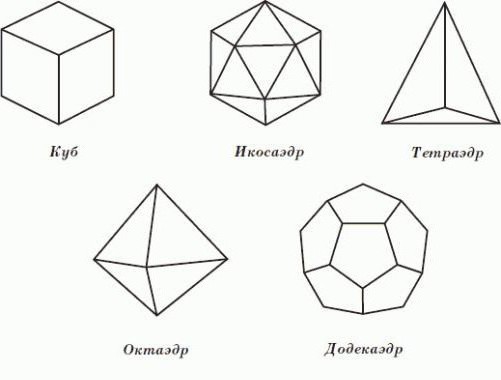
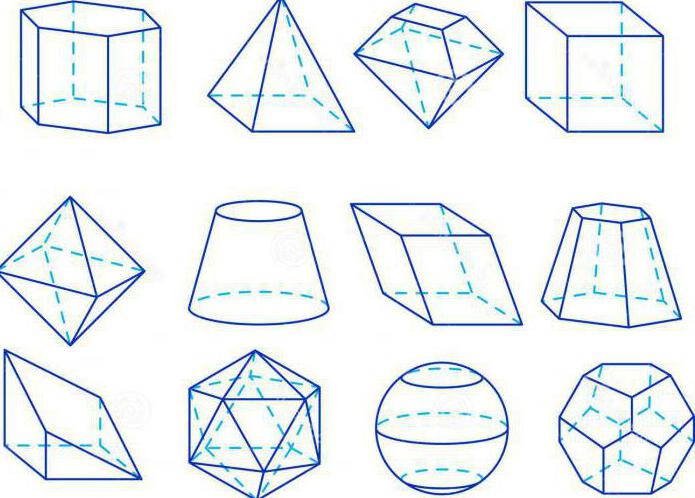
Jaka jest ta dyscyplina we współczesnym znaczeniu tego słowa? Geometria to nauka, która obejmuje różne teorie matematyczne. Zostały one historycznie opracowane na podstawie geometrii w jej pierwotnym znaczeniu, a ich konstrukcje wywodzą się z analizy, syntezy i modyfikacji jej zmian. Geometria w tym ogólnym sensie jest ściśle powiązana z innymi gałęziami matematyki, a jej granice nie są dokładne.