Wszystkie opcje, jak znaleźć obszar trapezowy
Wielościenny trapez ... Może być dowolny, równoramienny lub prostokątny. I w każdym przypadku musisz wiedzieć, jak znaleźć obszar trapezu. Oczywiście najprostszy sposób na zapamiętanie podstawowych formuł. Ale czasami łatwiej jest użyć tego, który pochodzi od wszystkich cech danego geometryczny kształt.
Kilka słów o trapezoidzie i jego elementach
Każdy czworobok, którego dwie boki są równoległe, można nazwać trapezem. Na ogół nie są równe i nazywane są zasadami. Większy z nich jest niższy, a drugi górny.
Pozostałe dwa boki są boczne. Dla arbitralnego trapezu mają różne długości. Jeśli są równe, liczba ta staje się równoramienna.
Jeśli nagle kąt pomiędzy bokiem a podstawą wynosi 90 stopni, wówczas trapez jest prostokątny.
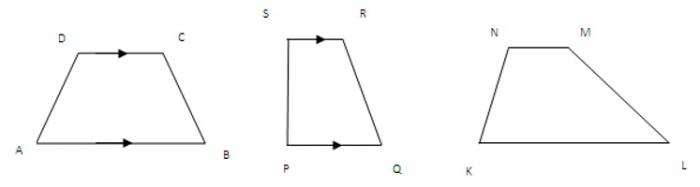
Wszystkie te cechy mogą pomóc w rozwiązaniu problemu znalezienia obszaru trapezu.
Wśród elementów tej figury, które mogą być niezbędne w rozwiązywaniu problemów, możemy wyróżnić następujące:
- wysokość, tj. odcinek prostopadły do obu zasad;
- środkowa linia, która ma końce środkowe.
W jaki sposób obliczyć obszar, jeśli znasz podstawę i wysokość?
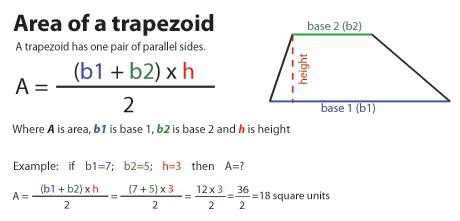
To wyrażenie jest podawane przez głównego użytkownika, ponieważ najczęściej można rozpoznać te wartości, nawet jeśli nie są one jawnie podane. Tak więc, aby zrozumieć, jak znaleźć obszar trapezu będziesz musiał złożyć obie bazy i podzielić je na dwie. Wynikowa wartość jest następnie mnożona przez wartość wysokości.
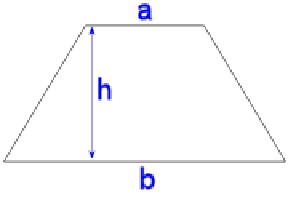
Jeśli oznaczymy podstawy literami a 1 i 2 , wysokość to n, wówczas wzór dla obszaru będzie wyglądał następująco:
S = ((a 1 + a 2 ) / 2) * n.
Wzór do obliczania obszaru, jeśli podano jego wysokość i środkową linię
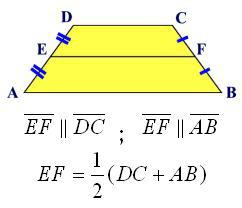
Jeśli przyjrzysz się dokładnie poprzedniej formule, łatwo zauważyć, że wartość średniej linii jest w niej wyraźnie widoczna. Mianowicie, suma podstaw podzielona przez dwa. Niech środkowa linia zostanie oznaczona literą l, wtedy formuła dla obszaru będzie następująca:
S = l * n.
Możliwość znalezienia obszaru po przekątnej
Ta metoda pomoże ci, jeśli znasz kąt, jaki tworzą. Załóżmy, że przekątne są oznaczone literami q 1 i g 2 , a kątami między nimi są α i β. Następnie wzór, jak znaleźć obszar trapezu, zostanie zapisany w następujący sposób:
S = ((d 1 * d 2 ) / 2) * sin α.
W tym wyrażeniu można łatwo zastąpić α przez β. Wynik nie ulegnie zmianie.
Jak się dowiedzieć, czy wszystkie strony figurki są znane?
Są też sytuacje, w których dokładnie te boki są znane na tej figurze. Ta formuła jest uciążliwa i trudna do zapamiętania. Ale jest to możliwe. Niech boki mają oznaczenie: w 1 i 2 , podstawa i 1 więcej niż 2 . Następnie wzór obszaru będzie wyglądał następująco:
S = ((a 1 + a 2 ) / 2) * √ {in 1 2 - [(a 1 - a 2 ) 2 + w 1 2 - w 2 2 ) / (2 * (a 1 - a 2 )) ] 2 }.
Sposoby obliczania powierzchni trapezu równoramiennego
Pierwsza związana jest z faktem, że można do niej wprowadzić koło. I znając jego promień (jest oznaczony literą r), a także kąt w podstawie - γ, można użyć następującej formuły:
S = (4 * r 2 ) / sin γ.
Ta ostatnia ogólna formuła, która opiera się na znajomości wszystkich stron rysunku, zostanie znacznie uproszczona, ponieważ strony mają to samo znaczenie:
S = ((a 1 + a 2 ) / 2) * √ {w 2 - [(a 1 - a 2 ) 2 / (2 * (a 1 - a 2 ))] 2 }.
Metody obliczania powierzchni prostokątnego trapezu
Oczywiste jest, że zrobi to dowolny z wymienionych dla dowolnego kształtu. Ale czasami warto wiedzieć o jednej z cech takiego trapezu. Polega ona na tym, że różnica kwadratów długości przekątnych jest równa różnicy składającej się z kwadratów zasad.
Często zapomina się o formułach trapezu, a zapamiętuje się wyrażenia dla obszarów prostokąta i trójkąta. Następnie możesz zastosować prosty sposób. Podziel trapez na dwa kształty, jeśli jest prostokątny, lub trzy. Jeden dokładnie będzie prostokątem, a drugi lub dwa pozostałe trójkąty. Po obliczeniu obszarów z tych liczb dodamy je tylko.
Jest to dość prosty sposób jak znaleźć kwadrat trapez.
Co jeśli współrzędne wierzchołków trapezu są znane?
W takim przypadku będziesz musiał użyć wyrażenia, które pozwoli ci określić odległość między punktami. Można go zastosować trzy razy: aby nauczyć się obu zasad i jednej wysokości. A następnie po prostu zastosuj pierwszą formułę, która jest opisana nieco wyżej.
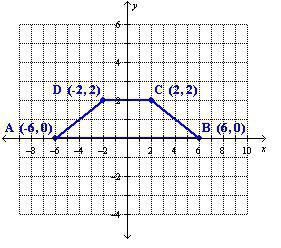
Aby zilustrować tę metodę, możesz podać przykład. Biorąc pod uwagę wierzchołki o współrzędnych A (5; 7), B (8; 7), C (10; 1), D (1; 1). Musisz znać obszar postaci.
Zanim znajdziesz obszar trapezu, musisz obliczyć długości bazowe za pomocą współrzędnych. Będziesz potrzebował następującej formuły:
długość segmentu = √ {(różnica pierwszych współrzędnych punktów) 2 + (różnica drugich współrzędnych punktów) 2 }.
Górna podstawa jest oznaczona AB, co oznacza, że jej długość będzie równa √ {(8-5) 2 + (7-7) 2 } = √9 = 3. Niższy będzie SD = √ {(10-1) 2 + (1-1 ) 2 } = √81 = 9.
Teraz musisz trzymać wysokość od góry do podstawy. Niech jego początek będzie w punkcie A. Koniec segmentu będzie na dolnej podstawie w punkcie o współrzędnych (5; 1), niech to będzie punkt N. Długość odcinka AN będzie równa √ {(5-5) 2 + (7-1) 2 } = √36 = 6.
Pozostaje tylko zastąpić uzyskane wartości wzorem formuły trapezu:
S = ((3 + 9) / 2) * 6 = 36.
Problem rozwiązano bez jednostek, ponieważ skala siatki współrzędnych nie została określona. Może to być milimetr lub metr.
Przykłady zadań
№ 1. Stan. Znany kąt między przekątnymi dowolnego trapezu, jest równy 30 stopni. Mniejsze przekątne to 3 dm, a drugie 2 razy większe. Konieczne jest obliczenie powierzchni trapezu.
Decyzja. Najpierw musisz znać długość drugiej przekątnej, ponieważ bez tego nie możesz policzyć odpowiedzi. Oblicz to łatwo, 3 * 2 = 6 (dm).
Teraz musisz użyć odpowiedniej formuły dla obszaru:
S = ((3 * 6) / 2) * sin 30º = 18/2 * ½ = 4,5 (dm 2 ). Problem rozwiązany.
Odpowiedź: powierzchnia trapezu wynosi 4,5 dm 2 .
№ 2. Stan. W trapezie AVSD podstawami są segmenty AD i BC. Punkt E jest środkiem boku SD. Z niego, prostopadle do prostej AB jest narysowany, koniec tego odcinka jest oznaczony literą N. Wiadomo, że długości AB i EH wynoszą odpowiednio 5 i 4 cm, konieczne jest obliczenie powierzchni trapezu.
Decyzja. Najpierw musisz zrobić rysunek. Ponieważ wartość prostopadłościanu jest mniejsza niż strona, na którą jest prowadzona, trapez będzie nieznacznie wydłużony do góry. Więc EN znajdzie się wewnątrz figury.
Aby wyraźnie zobaczyć postęp zadania, musisz wykonać dodatkową konstrukcję. Mianowicie, narysuj prostą linię, która będzie równoległa do boku AB. Punkty przecięcia tej linii z AD - P, oraz z kontynuacją sił zbrojnych - X. Wynikową liczbą jest równoległobok. Co więcej, jego powierzchnia jest równa pożądanej. Wynika to z faktu, że trójkąty, które pojawiły się z dodatkową konstrukcją są równe. Wynika to z równości boku i dwóch narożników sąsiadujących z nim, jedno - pionowe, drugie - leżące w poprzek.
Aby znaleźć obszar równoległoboku, możliwe jest zastosowanie wzoru, który zawiera iloczyn boku i wysokości, obniżonego na nim.
Zatem powierzchnia trapezu wynosi 5 * 4 = 20 cm 2 .
Odpowiedź: S = 20 cm 2 .
№ 3. Stan. Elementy trapezu równoramiennego mają następujące znaczenie: dolna podstawa ma 14 cm, górna 4 cm, a kąt ostry 45º. Konieczne jest obliczenie jego powierzchni.
Decyzja. Niech mniejsza podstawa będzie oznaczona jako BC. Wysokość zaczerpnięta z punktu B będzie nazywana HV. Ponieważ kąt wynosi 45º, trójkąt ABH będzie prostokątny i równoramienny. A więc AN = BH. Co więcej, NA jest bardzo łatwa do znalezienia. Jest równa połowie różnicy podstawowej. To jest (14 - 4) / 2 = 10/2 = 5 (cm).
Tereny są znane, liczy się wysokość. Możesz użyć pierwszej formuły, którą rozważano tutaj dla dowolnego trapezu.
S = ((14 + 4) / 2) * 5 = 18/2 * 5 = 9 * 5 = 45 (cm 2 ).
Odpowiedź: Wymagany obszar to 45 cm 2 .
№ 4. Stan. Istnieje arbitralne trapezowe AVSD. Po bokach są zbierane punkty O i E, tak że OE jest równoległy do podstawy arki. Powierzchnia trapezowego AOED jest pięciokrotnie większa od powierzchni CFE. Oblicz wartość OE, jeśli znane są długości podstawy.
Decyzja. Konieczne będzie narysowanie dwóch równoległych linii prostych AB: od pierwszego do C punktu, jego przecięcie z OE to punkt T; drugi do E i punkt przecięcia z AD będzie M
Niech nieznane OE = x. Wysokość mniejszego trapezu CFE wynosi n 1 , a większy AECO to n 2 .
Ponieważ obszary tych dwóch trapezów są powiązane jako 1 do 5, możemy napisać następującą równość:
(x + a 2 ) * n 1 = 1/5 (x + a 1 ) * n 2
lub
n 1 / n 2 = (x + a 1 ) / (5 (x + a 2 )).
Wysokości i boki trójkątów są proporcjonalne pod względem konstrukcji. Dlatego możemy napisać kolejną równość:
n 1 / n 2 = (x - a 2 ) / (a 1 - x).
W dwóch ostatnich pozycjach po lewej stronie są równe wartości, więc możesz napisać, że (x + a 1 ) / (5 (x + a 2 )) jest równe (x - a 2 ) / (a 1 - x).
Wymaga to szeregu przekształceń. Najpierw mnożyć w poprzek. Pojawią się nawiasy wskazujące różnicę w kwadratach, po zastosowaniu tej formuły otrzymasz krótkie równanie.
Należy otworzyć nawiasy i przenieść wszystkie terminy z nieznanego "x" na lewą stronę, a następnie wyodrębnić pierwiastek kwadratowy.
Odpowiedź : x = √ {(a 1 2 + 5 a 2 2 ) / 6}.