Podstawowe prawa prądu stałego: definicje i formuły
Prawo Ohma zostało sformułowane po raz pierwszy przez niemieckiego fizyka i matematyka Georga Simona Oma. Prawo Ohma jest podstawowym prawem dla obwodów elektrycznych z prądem stałym. Ustala związek pomiędzy napięciem lub spadkiem potencjału, natężeniem prądu i oporem w obwodzie. Przyjrzyjmy się prawu Ohma i innym podstawowym prawom prądu stałego.
Tło historyczne

Georg Simon Om urodził się w mieście Erlangen (Niemcy) 16 marca 1789 r. W rodzinie protestanckiej. Od wczesnego dzieciństwa zaczął pracować w warsztacie hydraulicznym swojego ojca. Kariera fizyki rozpoczęła się w Omme na Politechnice w Norymberdze. Do końca swoich dni wykładał fizykę na Uniwersytecie w Monachium.
Główną zaletą Ohma w fizyce jest to, że wprowadził i opisał taką fizyczną ilość jak rezystancja elektryczna. Najpierw sformułował w formie matematycznej związek między różnicą potencjałów, natężeniem prądu i oporem elektrycznym w obwodzie, dla którego jednostka ruchu oporu została nazwana po swoim nazwisku.
Nowe pomysły Ohma nie zostały natychmiast zaakceptowane przez światową społeczność naukową, dopiero w 1841 r. Royal Society w Londynie przyznało Medal Oom the Copley, aw 1849 r. Uniwersytet w Monachium przyznał mu Wydział Fizyki.
Om podczas swojej działalności naukowej zajmował się nie tylko obwodami elektrycznymi. W 1840 roku studiował fale dźwiękowe a od 1852 roku zajmował się optyką, w szczególności zjawiskiem interferencji. Naukowiec zmarł w Monachium 6 lipca 1854 roku.
Eksperymenty Ohma
Zanim Om przedstawił swoje słynne prawo prąd stały inni naukowcy przeprowadzili wiele eksperymentów z obwodami elektrycznymi. Należy zauważyć eksperymenty brytyjskiego Henry'ego Cavendisha, który badał zachowanie puszek Leiden w 1781 roku, ale nie był w stanie opublikować swoich wniosków.
Obecnie fizycy dysponują instrumentami pozwalającymi na pomiar dowolnych parametrów obwodu elektrycznego z niezbędną dokładnością, a pod koniec XVIII-XIX wieku nie było takich urządzeń, co utrudniało Ohmu odkrycie prawa prądu stałego.
Właśnie dlatego Om postanowił stworzyć takie urządzenie samodzielnie. W szczególności używał skalerów skrętnych Coulomba, ale udoskonalił je, dodając do nich element magnetyczny. W tym samym czasie naukowiec wykorzystał odkrycie Hansa Christiana Oersteda w 1819 roku z faktu, że przewodnik z prądem wywiera siłę na namagnesowaną igłę w jego pobliżu. Wykorzystując swoją nową równowagę skrętną, przewodząc kable o różnych długościach, źródło prądu elektrycznego i naczynia z rtęcią, Ohm był w stanie zmierzyć spadek siły, z jaką przewodnik z prądem działa na igłę, gdy wzrasta długość tego przewodnika.
W wyniku tych eksperymentów naukowiec uzyskał następującą matematyczną zależność: V = 0,41 lg (1 + x), gdzie V jest napięciem w obwodzie, x jest długością przewodnika z prądem. Wyrażenie to doprowadziło następnie naukowca do sformułowania prawa prądu stałego.
Pojęcie siły prądu elektrycznego
Przed rozważeniem prawa Ohma dla prądu stałego wprowadzamy pojęcie aktualnej siły. Niektóre cząsteczki w przyrodzie mają tak zwany ładunek elektryczny. Pojęcie natężenia prądu jest bezpośrednio związane z ruchem tych naładowanych cząstek, które w większości przypadków są albo jonami, albo elektronami. Przez prąd w fizyce rozumie się ilość ładunku przechodzącego przez sekcję przewodnika na jednostkę czasu, która jest matematycznie wyrażana jako następujące wyrażenie: I = dq / dt.
Jednostką natężenia prądu w SI jest amper (A), 1 A to natężenie prądu, przy którym ładunek 1 C jest przesyłany przewodnikiem przez 1 s. Ponieważ ładunki dodatnie i ujemne poruszają się w przeciwnych kierunkach w tym samym polu elektrycznym, zwykle określa się natężenie prądu przez kierunek ruchu ładunków dodatnich.
Prędkość ruchu naładowanych cząstek w polu elektrycznym

W fizyce sformułowano prawo prądu stałego dla I = const, co oznacza, że każda cząstka przenosząca ładunek elektryczny musi poruszać się ze stałą prędkością. Jednakże, aby istniał prąd elektryczny, konieczne jest naładowanie cząsteczek zdolnych do poruszania się, jak również istnienie pola elektrycznego. Ten ostatni działa na ładunek elektryczny q z określoną siłą. Siła ta jest określona wzorem: F = q * E, tutaj E jest natężeniem pola elektrycznego.
Zgodnie z drugim prawem Newtona naładowana cząstka uzyskuje przyspieszenie a = q * E / m, gdzie m jest masą cząstki. Ponieważ wszystkie wartości w tym wyrażeniu są stałe, wówczas przyspieszenie będzie również stałe i niezerowe. Wszystkie te argumenty są słuszne w przypadku ładunku poruszającego się w pustej przestrzeni, ale jeśli porusza się w jakimkolwiek medium, to z nośnika powstaje pewien opór.
Na przykład, elektron poruszający się pod działaniem siły elektrycznej w przewodniku metalowym doświadcza ciągłych zderzeń z jonami tworzącymi metalową sieć krystaliczną. Te kolizje powodują, że elektron porusza się ze stałą prędkością, która jest nazywana prędkością dryftu. W interakcji elektronu z jonami kratowymi leży natura oporu elektrycznego.
Ruch elektronu w przewodniku metalowym można porównać z ruchem kropli deszczu w powietrzu, ponieważ spadek ten nie spada wraz z przyspieszeniem swobodnego spadania, ale powoduje równomierny ruch z powodu wpływu siły oporu z powietrza.
Prawo Lokalnego Ohma
W każdej szkole zaczynają się uczyć praw DC w klasie 8. Jednocześnie sformułuj prawo Ohma, najpierw w formie lokalnej. Aby to zrobić, weź na przykład metaliczny przewodnik.
W metalu, elektrony walencyjne, czyli elektrony umieszczone na zewnętrznej powłoce atomowej atomów, są słabo związane z jądrami atomowymi, dlatego w materiale masowym nie należą do konkretnego jądra atomowego, ale są wolne lub zsocjalizowane. Każdy taki elektron w temperaturze pokojowej porusza się chaotycznie w metalowym krysztale. Ten ruch jest podobny do ruchu cząsteczki w gazie. Prędkość ruchu termicznego elektronu jest duża, wynosi około 10 6 m / s. Ponieważ ruch jest równie prawdopodobny we wszystkich kierunkach, nie powoduje wzrostu prądu elektrycznego.
Prąd pojawia się, jeśli ten przewodnik jest umieszczony w polu elektrycznym. W wyniku tego elektron uzyskuje prędkość dryfu, której rząd wielkości wynosi 10 -6 m / s. W wyniku tego prąd elektryczny przechodzący przez pole przekroju A jest zapisany jako następujący wzór: I = n * q 2 * E * t * A / m e , tu n to liczba elektronów przechodzących przez obszar A w czasie t, który jest czasem pomiędzy dwie zderzenia elektronów z jonami sieci, m e - masa elektronowa
Wynikowe wyrażenie można zapisać w postaci J = I / A = σ * E, gdzie J jest gęstością prądu elektrycznego, σ jest właściwością materiału, którą nazywa się przewodnością elektryczną. To wyrażenie gęstości prądu nazywa się prawem Ohma dla prądu stałego w formie lokalnej.
Prawo Ohma w makroskopowej formie

W szkole w klasie 8 prawo prądu stałego jest również rozpatrywane w formie makroskopowej. Można go łatwo uzyskać z odpowiedniego prawa w lokalnej formie. Aby to zrobić, konieczne jest określenie napięcia lub potencjalnego spadku w obwodzie elektrycznym jako następującego wyrażenia: ΔV = E * l, gdzie l jest długością przewodu z prądem, a ΔV jest napięciem na jego końcach.
W rezultacie prawo Ohma przyjmie postać: ΔV = I * l / (σ * A) = R * I, gdzie R jest oporem elektrycznym. Jak widać z prawa bezpośredniego prądu elektrycznego w postaci makroskopowej, wartość R jest odwrotnością przewodności elektrycznej σ, tj. Im lepiej materiał przewodzi, tym mniejszy jest jego opór elektryczny. Należy również zauważyć, że podczas gdy σ jest właściwością materiału, z którego wykonany jest przewodnik, R jest właściwością konkretnego przewodnika i zależy nie tylko od materiału, ale także od jego parametrów geometrycznych (długość i pole przekroju).
Zastosowanie i znaczenie klasycznego prawa Ohma
Prawo Ohma w klasycznej lub makroskopowej formie zapisane jest w formie: V = I * R. W przypadku metali R jest wartością stałą, niezależnie od natężenia prądu płynącego przez przewodnik. Jednak w przypadku niektórych materiałów, takich jak półprzewodniki, tak nie jest. Materiały, w których oporność elektryczna jest stała, nazywane są liniowymi lub omowymi. Dla nich charakterystyka prądowo-napięciowa, czyli funkcja napięcia w funkcji prądu U (I), jest liniowa.
Prawa Ohma nie można uznać za fundamentalne prawo natury, ponieważ jest ono ważne tylko dla pewnej klasy materiałów, głównie metali. Odgrywa on jednak ważną rolę w fizyce i życiu codziennym, ponieważ pozwala nam w prosty sposób określić ważne wielkości fizyczne w obwodzie elektrycznym. W szczególności, dzięki prawu Ohma, obwód stałoprądowy oblicza stratę energii elektrycznej podczas jej transmisji i zużycia. Prawo Ohma służy również do obliczania wymaganej wartości rezystancji, która powinna być zawarta w obwodzie elektrycznym, aby wykonywała swoje funkcje z maksymalną wydajnością.
Zależność oporu od temperatury dla materiałów omowych
Biorąc pod uwagę prawa obwodów prądu stałego, należy wspomnieć o tym, jak zmienia się opór wraz ze wzrostem temperatury. Analogicznie do przewodności elektrycznej materiału w fizyce wprowadzono pojęcie rezystancji elektrycznej ρ, która jest związana z opornością za pomocą następującego wzoru: R = l * ρ / A.
Zostało ustalone empirycznie, że dla materiałów omowych, ρ spełnia następującą zależność temperaturową: ρ = ρ 0 * [1 + α (TT 0 ) + β (TT 0 ) 2 + ...], tu ρ 0 to opór właściwy tego materiału z temperatura T0, która często przyjmuje się, że wynosi 20 ° C.
W przypadku materiałów metalicznych w zakresie od 0 do 200 ° C rezystywność liniowo zależy od temperatury, tj. Ρ = ρ 0 * [1 + α (TT 0 )], gdzie α jest współczynnikiem rezystancji temperaturowej, który jest wartością dodatnią dla metali, sugeruje, że opór elektryczny wzrasta liniowo wraz ze wzrostem temperatury metali. Zachowanie to wiąże się ze spadkiem odległości, którą elektron pokonuje między dwoma zderzeniami z jonami sieciowymi ze wzrostem temperatury.
Warto zauważyć, że w półprzewodnikach rezystywność zmniejsza się wraz ze wzrostem temperatury. Fakt ten jest związany ze wzrostem liczby nośników prądu elektrycznego podczas ogrzewania materiału półprzewodnikowego, na przykład krzemu lub germanu.
Prawa Kirchhoffa

W szkołach w klasie 10 prawa prądu stałego nie są ograniczone do prawa Ohma. Szkolny program studiuje także prawa Kirchhoffa. Istnieją dwa prawa Kirchhoffa dotyczące prądu stałego. Są oparte na prawo zachowania energii i ładować w obwodzie elektrycznym. Poniżej znajdują się sformułowania dotyczące obu praw Kirchhoffa:
- Dla dowolnego węzła obwodu elektrycznego suma wszystkich prądów wchodzących do tego węzła jest równa sumie prądów, które go opuszczają. To sformułowanie odzwierciedla prawo zachowania ładunku.
- W obwodzie zamkniętej pętli suma wszystkich spadków napięcia na elementach tego obwodu jest równa napięciu, które jest do niego doprowadzane. Drugie prawo Kirchhoffa odzwierciedla zachowanie energii potencjalnej w obwodzie elektrycznym.
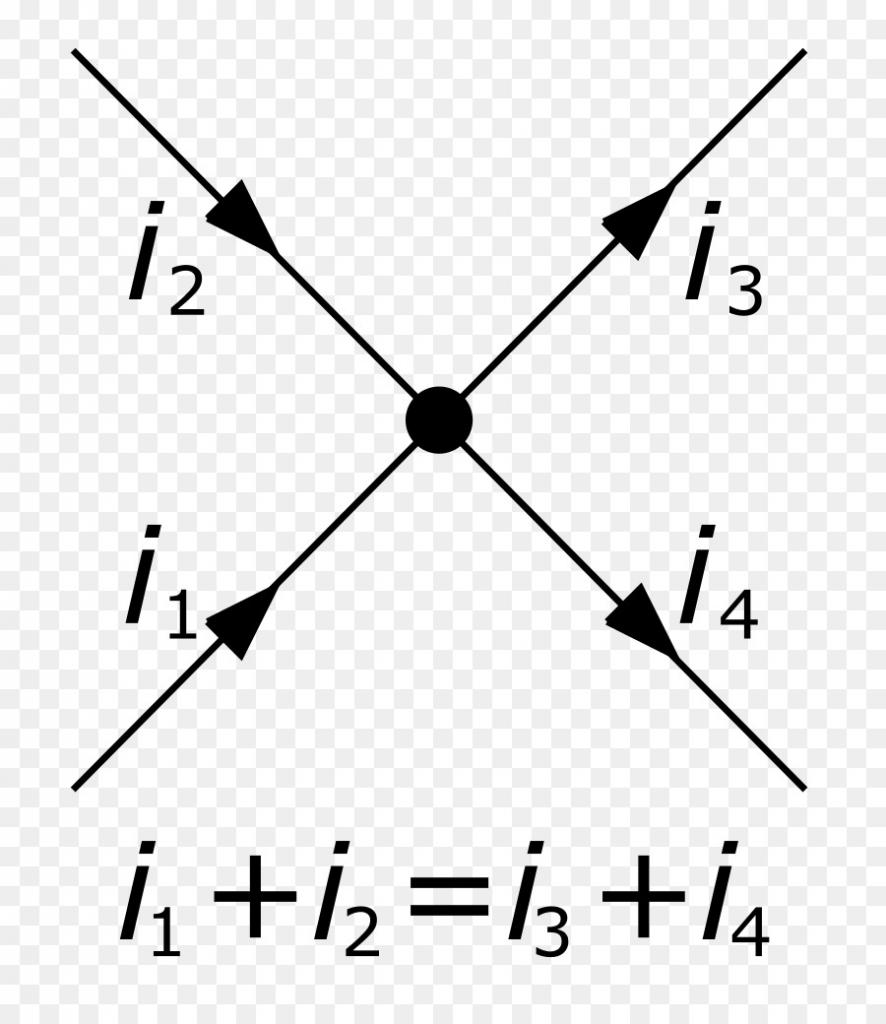
Prawa te zostały po raz pierwszy zarejestrowane w 1846 roku. Obecnie są one szeroko stosowane w elektrotechnice i elektronice do określania nieznanych prądów, napięć i rezystancji w obwodach. Należy zauważyć, że w przypadku obecności niezerowego oporu elektrycznego w obwodzie R część energii elektrycznej zamieni się w ciepło Q, które nazywa się Joule i jest obliczane za pomocą wzoru Q = I 2 Rt, gdzie t jest czasem prądu płynącego przez element obwodu z rezystancją R.
Praktyczne zastosowanie praw Ohma i Kirchhoffa
Podajemy przykład problemu z prawami prądu stałego. Poniższy rysunek pokazuje przykład obwodu elektrycznego, który składa się z dwóch obwodów, dwóch źródeł napięcia i 5 rezystorów o różnych oporach. Zadanie polega na znalezieniu nieznanych prądów Ix i ja. Od razu należy powiedzieć, że kierunek w obu konturach jest wybierany arbitralnie, w tym przypadku zgodnie z ruchem wskazówek zegara.
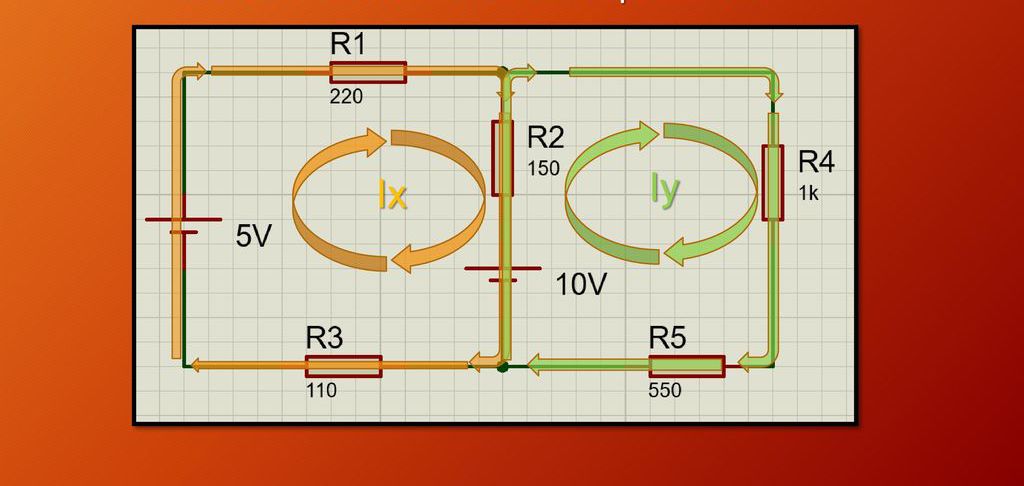
Następnie należy rozważyć każdy obwód osobno. Na początek zwróć uwagę na obwód o nieznanym prądzie I x . Dla wybranego obwodu konieczne jest zastosowanie drugiego prawa Kirchhoffa, to jest prawa, które mówi, że napięcie spada na wszystkie rezystory, a napięcie zasilania ze wszystkich źródeł prądu jest równe. Stosując to prawo otrzymujemy: 5-10 = I x * R 1 + (I x -I y ) * R 2 + I x * R 3 . Podczas kompilacji tego wyrażenia brano pod uwagę znak wybranego kierunku prądu Ix jako kierunku dodatniego, dlatego różnica potencjałów przy źródle 5 V jest dodatnia, a przy źródle 10 V ujemna. Należy również zauważyć, że rozważając ten obwód, należy wziąć pod uwagę prąd Iy, który płynie zgodnie z wprowadzonymi symbolami przez rezystor R2.
Teraz otrzymujemy podobne równanie dla drugiego obwodu z nieznanym prądem Iy . To wyrażenie będzie miało postać: 10 = (I-Ix) * R 2 + I y * R 4 + I y * R 5 . W drugim obwodzie jest tylko jedno źródło zasilania (10 V), dlatego tylko wchodzi ono w wyrażenia wyprowadzone z 2. Prawa Kirchhoffa.
W ten sposób uzyskuje się dwa równania, w których występują dwie niewiadome: Ix i Iy . Pozostaje połączyć te wyrażenia w układ równań liniowych i rozwiązać go. Poniższy rysunek pokazuje dany obwód i wynikowy układ równań do wyznaczania nieznanych prądów.
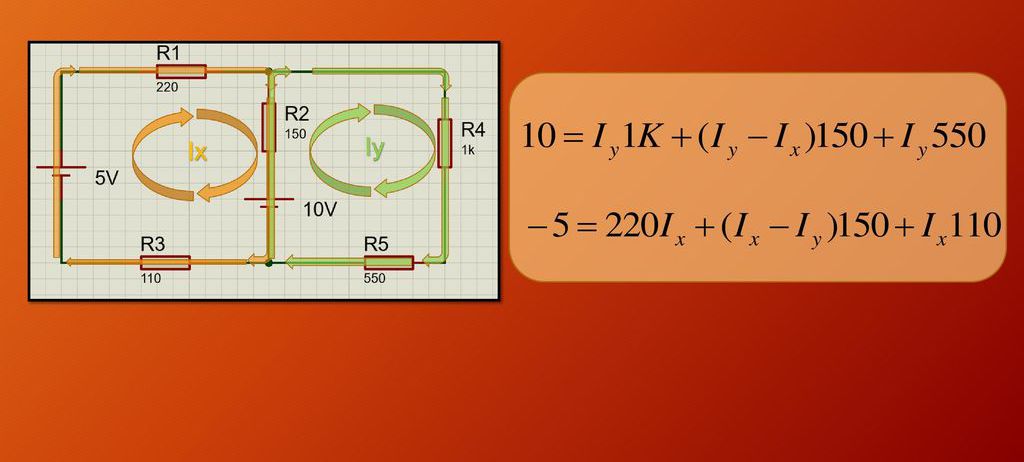
Rozwiązując układ równań, otrzymujemy, że I x = -0,00882 A = -8,82 mA, a ja y = 0,0051 A = 5,1 mA. Znak minus wskazuje, że w rzeczywistości prąd płynie w kierunku przeciwnym do wybranego. W wyniku tego przez rezystory R 1 , R 3 przepływa prąd o wartości 8,82 mA przez rezystory R 4 , R 5 - 5,1 mA i przez rezystor R 2 - I y - I x = 13,92 mA.