Przykład algorytmu Diffiego Hellmana
Ujawnienie tematu kryptografii klucza publicznego musi się rozpocząć od historycznej ścieżki problemu. Whitfield Diffie i Martin Hellman jako pierwsi pytali o otwartą metodę przekazywania kluczy. Stało się to w 1976 roku. Publikacja podjęła pierwsze próby rozwiązania tego problemu. Ich rozwiązanie nie było pozbawione wad, ale położyło fundament pod zupełnie odmienny sposób myślenia w dziedzinie szyfrowanego przesyłania danych.
Wymagania wstępne dotyczące tworzenia algorytmu Diffie-Hellmana
Do tego momentu uwierzytelnianie i szyfrowanie były możliwe tylko za pośrednictwem wspólnego tajnego klucza. Wraz z rozwojem technologii sprawa stała się bardziej paląca. Jeśli 10 osób będzie musiało przesyłać dane między sobą za pośrednictwem niezabezpieczonych kanałów, będą musiały wymieniać hasła ze sobą. To zadanie wygląda całkiem realnie. Nawet z koniecznością ich aktualizacji. W końcu dla 10 znajomych potrzebujesz tylko 45 tajnych kluczy. A jeśli kontakty będą miały 100? Zajmie 4950 haseł. Sytuacja rośnie jak śnieżka.
Głównym osiągnięciem Diffiego i Hellmana było właściwe sformułowanie pytania i pomysłowa odpowiedź na to pytanie. Zasugerowali, że dane mogą zostać zaszyfrowane w jeden sposób i odszyfrowane w innym. Oznacza to, że mają 2 klucze. Ta używana do szyfrowania może pozostać otwarta. W ten sposób każda osoba może zaszyfrować wiadomość, ale tylko właściciele drugiego tajnego klucza mogą ją odszyfrować. Ale jak wdrożyć algorytm transferu takiego klucza? Naukowcy byli w stanie częściowo i dać odpowiedź.
Krótka matematyka: grupy
Algorytm lub protokół Diffiego-Hellmana (dalszy DH) działa za pomocą liczb pierwszych. Niech to będzie wystarczająco duży numer należący do zestawu liczby pierwsze. Algorytm obejmuje użycie liczby 250-500 bajtów. Niech Za będzie multiplikatywną grupą pierścienia reszt modulo a, która będzie używana przez algorytm szyfrowania Diffiego-Hellmana. Składa się z zestawu liczb 1, ..., a-1.
Weźmy jakiś element b z grupy Z a i rozważmy nieskończoną sekwencję 1, b, b 2 , b 3 , b 4 , ... Z faktu, że grupa Z a jest z definicji skończonym zbiorem, prędzej czy później rozważana sekwencja {b} zacznie się powtarzać. Ustaw b i = b j (i <j).
Teraz dzielimy każdą część równości przez b i (modulo a) i otrzymujemy b ji = 1. Oznacza to, że istnieje liczba k = ji, dla której b k = 1 (mod a) jest prawdziwa. Najmniejsze k, dla którego ta równość się trzyma, nazywa się porządkiem b. Aby uniknąć pomyłki z inną literaturą specjalną, do wyjaśnienia systemu Diffiego-Hellmana używa się standardowej notacji matematycznej.
Zatem, podnosząc liczbę b, nazywaną elementem generującym, do mocy, otrzymujemy sekwencję liczb (zestaw) 1, ..., b k-1 . Liczba elementów w tym zestawie to dokładnie k.
Modulo właściwości multiplikacji a mówi, że istnieje co najmniej jedna liczba b generująca wszystkie elementy grupy Z * a . Innymi słowy, istnieje liczba, dla której k = a-1 jest prawdziwa Ta właściwość pozwala nam reprezentować liczby grupy Z * a w postaci 1, b, b 2 , ... b a-2 . Taka liczba b nazywana jest prymitywną liczbą grupy.
W dalszej części łatwo jest dowieść na podstawie znaków grupy, że zbiór generowany przez liczbę b jest także samą grupą i dziedziczy wszystkie właściwości grup. Innymi słowy operacje w wygenerowanej grupie lub podgrupie mogą być wykonywane dokładnie w taki sam sposób, jak w grupie modulo a.
Rozważ stwierdzenie. Dla dowolnego elementu b jego kolejność jest dzielnikiem a-1. Łatwo to pokazać. Niech a = 7. Liczba b = 3 jest prymitywna, ponieważ 1, ..., b 5 = 1, 3, 2, 6, 4, 5. Wtedy liczba h = 2 wygeneruje podgrupę 1, ..., h 2 = 1 , 2, 4, ponieważ h 3 = 2 3 mod 7 = 1. h = 6 generuje podgrupę 1, 6. Rozmiary grup wynoszą odpowiednio 3 i 2. Oczywiście są one dzielnikami liczby a-1 = 6.
Pierwszy algorytm DH
W oryginalnej wersji algorytm działał w następujący sposób. Duża liczba a jest wybrana ze zbioru prostego i prymitywnego elementu b generującego Z * a . Obie liczby a i b reprezentują klucz publiczny, są one znane wszystkim, w tym atakującym. Jak ukryć wiadomości?
Na tym etapie Diffie i Hellman wymyślili bardzo pomysłowy ruch. Załóżmy, że mamy dwie osoby, które komunikują się ze sobą: A i B. Najpierw A wybiera losową liczbę x z Z * a , co jest równoważne wybraniu liczby z {1, ..., a-1}. Następnie oblicza wartość za pomocą formuły (b x mod a) i wysyła ją do B. Z kolei B wybiera pewną liczbę y z tego samego zestawu, oblicza wartość (b y mod a) i wysyła wynik z powrotem do A.
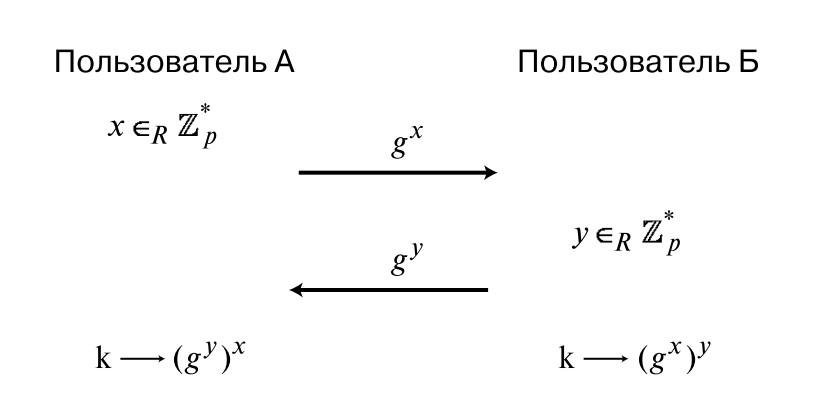
W tak trudny sposób okazuje się, że tajny klucz wygląda jak b xy . Ze względu na właściwość stopni, która mówi g xy = (g y ) x , rozmówca A może obliczyć żądaną wartość i odszyfrować przesłane do niego informacje. I w ten sam sposób ta wartość jest obliczana przez rozmówcę B. Zatem oba mają ten sam tajny klucz.
Jakie problemy napotyka intruz z tą wymianą informacji? Może przechwytywać liczby g x i g y . I nawet przy znajomości kluczy publicznych problem obliczania g xy nie jest trywialny, t. Ponieważ nie ma skutecznego algorytmu do znalezienia pożądanej wartości w dystrybucji kluczy Diffiego-Hellmana. Ten problem jest znany jako problem obliczania dyskretnego logarytmu.
Atak mediatora
Jedną ze słabości podstawowego algorytmu Diffiego-Hellmana jest jego podatność na ataki pośredników. Co to znaczy? Interlokutor A wie, że komunikuje się z pewną twarzą, ale konkretnie z kim - nie ma pojęcia. W ten sposób atakujący może przeniknąć do transferu informacji i naśladować rozmówcę B podczas komunikowania się z A i odwrotnie. Żadne z nich nie będzie mogło podejrzewać, że coś jest nie tak.
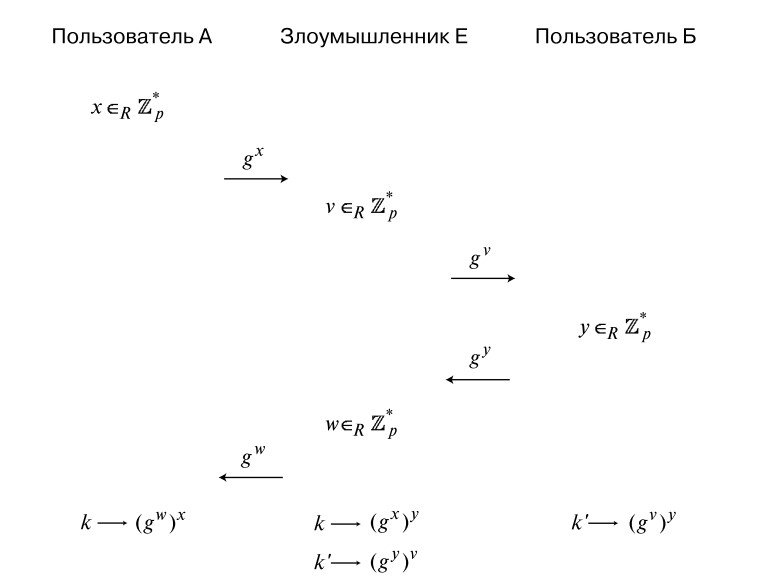
Jest tylko jeden obszar użycia, w którym wykluczone są ataki na algorytm Diffiego-Hellmana. To jest połączenie telefoniczne i wideo. Tutaj rozmówcy są w stanie poznać się nawzajem, więc mediator nie będzie w stanie przeniknąć.
Pułapki
Oprócz ataku mediatora, protokół DH zawiera wiele innych problemów. Na przykład jedną z wad jest sytuacja, w której prymityw nie jest prymitywny. Następnie generuje tylko podgrupę. Z powodu zawężenia liczby możliwych opcji atakujący otwiera możliwość ich wyszukiwania.

Problemów wynikających z tego niedociągnięcia można uniknąć, jeśli każdy z rozmówców sprawdza, czy liczby a i b są poprawne przed rozpoczęciem wymiany danych. Oznacza to, że a jest liczbą pierwszą, a b jest prymitywną. Jednakże, jeśli chodzi o bezpieczeństwo poprzez wdrożenie pewnych jednolitych, opcjonalnych kroków, użytkownicy często je ignorują.
Kolejny poważny problem powstaje na podstawie podgrup modulo a. Jeśli atakujący zdecyduje się zmienić g x na 1, aby ułatwić podsłuchiwanie, użytkownicy mogą łatwo go wykryć, sprawdzając numer pod kątem dopasowania. Jeśli jednak zastąpi klucz niskim numerem porządkowym, użytkownicy nie będą mogli niczego podejrzewać. A ponieważ liczba elementów w zestawie o niskiej kolejności będzie mała, atakujący będzie musiał uporządkować małą liczbę opcji do dekodowania.
Niezawodność liczb pierwszych
Algorytm DH wykorzystuje dużą i niezawodną liczbę wielu prostych. Jak dokładnie to wybrać? Analizujemy te kroki.
- Używając wzoru a = 2k + 1, wybierz liczby a i k tak, aby były proste.
- Z zestawu 1, ..., a-1, wyklucz 1 i a-1.
- Weź losową liczbę x z zestawu pozostałych po drugim kroku i znajdź wartość b = x 2 (mod a).
- Upewnij się, że b nie jest równe 1 lub a-1. Jeśli b jest równe jednej z niedozwolonych wartości, powinieneś wybrać inne x. I powtórz operację.
Otrzymany w ten sposób zestaw (a, k, b) można uznać za wystarczający do użycia w algorytmie wymiany kluczy Diffiego-Hellmana. W związku z tym odbiorca wiadomości musi również sprawdzić wartość, która musi być potęgą b, i upewnić się (na przykład, że funkcja symbolu Legendre), że wpada w zestaw generowany przez liczbę b.
Korzystanie z podgrup
Główną wadą powyższego algorytmu jest niewystarczająca wydajność. Zakładając, że długość pierwszej liczby a to n bitów, to k jest liczbą n-1. Okazuje się, że wszystkie stopnie będą n-1 długie. Następnie operacja potęgowanie średnio składa się z 3n / 2 multiplikacji mod a. To dość duży proces.

Aby poradzić sobie z tym problemem, zdecydowano się na użycie mniejszych podgrup. Jaki jest wzrost wydajności w tym przypadku? Jeśli liczba a składa się z 2000 bitów, do obliczenia b x wymagane są 3000 operacji mnożenia. Poprzez użycie podgrup można tę liczbę zmniejszyć do ~ 400. Ten znaczny wzrost wydajności algorytmu umożliwia jego pełne zastosowanie. Na przykład algorytm Diffie-Hellman z trzema lub więcej członkami.
Jaka powinna być długość a
Właściwy dobór rozmiarów parametrów algorytmu Diffiego-Hellmana jest dość skomplikowanym zadaniem. Powszechnym wymogiem w świecie kryptografii jest na przykład warunek, że atakujący potrzebuje co najmniej 2128 kroków, aby włamać się do systemu. Jeśli w symetrycznych algorytmach szyfrowania spełnienie takiego wymogu jest dość łatwe, w algorytmach klucza publicznego jest to prawdziwy problem. Jeśli spełniasz powyższe wymaganie, wówczas długość musi składać się z co najmniej 850 bajtów.

W praktyce rozmiar ten powoduje duże problemy z wydajnością w systemie, ponieważ operacje klucza publicznego trwają znacznie dłużej niż na przykład w szyfrowaniu symetrycznym z kluczami 128- lub 256-bitowymi. Więc jak być? Minimalna długość klucza publicznego musi zaczynać się od 2048 bitów. Im dłuższy klucz, tym wyższy poziom bezpieczeństwa. Należy wziąć pod uwagę przede wszystkim wydajność systemu i jego koszt. Jeśli pozwala ci użyć klucza 4096 bitów, musisz to zrobić.
W jaki sposób ocenia się wymagany poziom bezpieczeństwa?
Kluczowe rozmiary szyfrowania symetrycznego pozostają niezmienione (128, 256 bitów) przez cały okres istnienia systemu, podczas gdy rozmiary klucza publicznego są zawsze wartością zmienną. Jeśli musisz opracować system, który musi być używany przez 30 lat i zachować dane w tajemnicy przez co najmniej 20 lat po wyjęciu systemu z użycia, to rozmiar symetrycznego klucza szyfrowania musi początkowo być wystarczająco duży, aby chronić system przez następne 50 lat.
Ze względu na oczywiste problemy z wydajnością, ponieważ algorytm Diffie-Hellmana szyfruje znacznie większą liczbę operacji, wymagania dla kluczy publicznych różnią się. Pozostaje ważna przez jeden rok i chroni dane przez następne 20 lat, to jest w sumie 21 lat. Ze względu na zmienny rozmiar klucz można zmieniać co roku i tworzyć coraz dłużej w celu zapewnienia wymaganego poziomu bezpieczeństwa.
Na przykład najlepsze oszacowania pokazują, że klucz o długości 256 bajtów jest w stanie zapewnić ochronę danych przez około 20 lat, długość 384 bajtów wynosi 35 lat, a długość 512 bajtów to 47 lat itp. Liczba ta wynosi 6800 bitów, co zapewnia, że atakujący Aby go złamać, trzeba wykonać 2128 kroków, pochodzących z podobnych szacunków. Jest to jednak tylko prognoza, z którą trzeba bardzo uważać. Możesz dość dokładnie przewidzieć rozwój wydarzeń na 10 lat, ale w wieku 50 lat - to fantastyczne.
Praktyczne zalecenia
Oto kilka praktycznych wskazówek dotyczących korzystania z protokołu DH. Wybierz k jako pierwszą liczbę 256 bitów. Jest to minimum, które może zapewnić przynajmniej odpowiedni poziom bezpieczeństwa przed atakami. Dla a, wybierz liczbę, która miałaby postać Na + 1, gdzie N jest liczbą całkowitą. O rozmiarze numeru a powiedziano wcześniej. Następnie wybiera się losową liczbę b i sprawdza pod kątem kilku warunków. Po pierwsze, nie może być jednostką. Po drugie, b k = 1.
Z kolei każdy uczestnik komunikacji powinien być przekonany o:
- a i k są liczbami pierwszymi, długość k wynosi 256 bitów, a długość p jest dość duża.
- liczba k jest dzielnikiem a-1.
- b nie jest równe 1 i b k = 1.
Warunki te należy sprawdzić nawet przy bezwarunkowym zaufaniu do źródła.
Wniosek
Algorytm DH jest genialnym rozwiązaniem jednego z poważnych problemów i nadal jest aktywnie wykorzystywany w zmodyfikowanej formie dla nowoczesnych wymagań bezpieczeństwa w różnych protokołach. Algorytm Diffie-Hellmana jest na przykład używany w niektórych częściach implementacji protokołu IKE. Jednak jego stosowanie powinno być metodyczne i ostrożne ze względu na obecność oczywistych problemów i poważnych pułapek.