Dowody i własności kątów pionowych
Dwie linie przecinające się w jednym punkcie znajdują się nie tylko w matematyce, ale także w życiu codziennym. Możemy je obserwować, patrząc na nożyczki, na dwie skrzyżowane proste gałęzie drzew. Regularnie spotykamy się z nimi w obiektach architektonicznych, mechanice, w różnych mechanizmach i innych obiektach. Przykładami mogą być masa. Utworzone rogi na przecięciu stanowią podstawę geometrii i są badane przez dzieci w klasach średnich.

Określanie kątów pionowych w matematyce
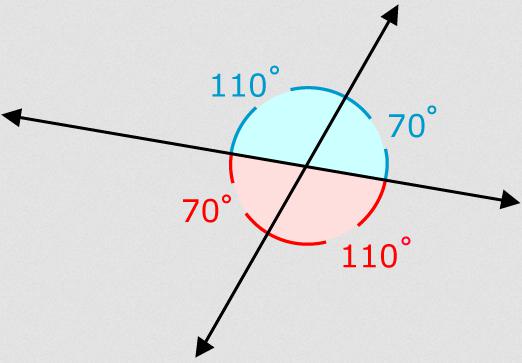
Kąty pionowe to dwa kąty utworzone przez przecięcie dwóch linii prostych w jednym punkcie. Boki jednego rogu w tym przypadku są zawsze kontynuacją drugiego. Zatem kąty pionowe są przeciwległe do siebie w przecinających się liniach prostych ze wspólnym punktem przecięcia.
Właściwości kąta pionowego
Rozwiązując różne problemy w geometrii, dziecko musi najpierw ustalić, z czym ma do czynienia. To przede wszystkim bada kształt postaci, z którą zaczyna pracę. W tym celu opiera się na właściwościach wszystkich swoich słynnych postaci. Właściwości kątów pionowych pomagają w prosty sposób stworzyć algorytm w głowie w celu rozwiązania problemu:
- Dwie linie proste, przecinające się w jednym punkcie, tworzą dwie pary kątów.
- Kąty pionowe ułożone naprzeciw siebie są równe.
- Suma wszystkich kątów na przecięciu dwóch linii prostych w jednym punkcie wynosi 360 °.
- Sąsiednie kąty tworzą połowę kątów pionowych.
Podczas budowania linii prostych z jednym punktem przecięcia powstają dwa kąty pionowe i cztery sąsiednie. Jednym z dowodów równości kątów pionowych jest równość sumy stopni 1 + 2 kątów i 3 + 4. W obu kątach sąsiednich i pionowych, jeśli znany jest jeden z kątów, drugi można obliczyć w prosty sposób. Wiedząc, jakie właściwości mają kąty pionowe, możesz szybko określić drugi kąt. Jeśli odejmiemy znany kąt od 180 °, wtedy poznamy wielkość drugiego.