Pełne przyspieszenie i jego komponenty. Przyspieszenie styczne i normalne przyspieszenie. Formuły i przykładowe rozwiązywanie problemów

W kinematykach, aby jednoznacznie określić charakterystykę ruchu ciała w dowolnym punkcie trajektorii, konieczne jest poznanie jego prędkości i przyspieszenia. Zależność czasowa tych ilości dostarcza wszystkich informacji niezbędnych do obliczenia drogi przebytej przez ciało. Rozważmy bardziej szczegółowo w artykule, czym jest przyspieszanie styczne i normalne przyspieszenie.

W fizyce

Przed rozważeniem przyspieszenia ruchu mechanicznego, przyspieszenia normalnego i stycznego, zapoznajmy się z samą koncepcją fizyczną. Definicja przyspieszenia jest dość prosta. W fizyce, pod tym pojęciem rozumie charakterystyczną zmianę prędkości. Ta ostatnia jest wielkością wektora, która określa prędkość zmiany współrzędnych poruszającego się obiektu w przestrzeni. Prędkość jest mierzona w metrach na sekundę (przebyta odległość na jednostkę czasu). Jeśli jest oznaczony symbolem v¯, to matematyczna definicja przyspieszenia a¯ będzie wyglądać następująco:

a¯ = dv¯ / dt

Ta równość określa tak zwane pełne chwilowe przyspieszenie. Nazywa się to natychmiast, ponieważ charakteryzuje zmianę prędkości tylko w danym momencie.

Jeśli ruch jest równomiernie przyspieszony, to znaczy, że przez długi czas przyspieszenie nie zmienia swojego modułu i kierunku, możemy zapisać następującą formułę, aby to ustalić:

a¯ = Δv¯ / Δt

Gdzie Δt >> dt. Wartość tu nazywana jest średnim przyspieszeniem, które na ogół różni się od chwilowego.

Przyspieszenie mierzone jest w systemie SI w metrach na sekundę (m / s ² ).

Trajektoria i komponenty pełnego przyspieszenia

Najczęściej ciała w naturze poruszają się po zakrzywionych trajektoriach. Przykładami takiego ruchu są: obrót planet na ich orbitach, paraboliczne opadanie kamienia na ziemi, zwrot samochodu. W przypadku trajektorii krzywoliniowej w dowolnym momencie prędkość jest kierowana stycznie do danego punktu trajektorii. W jaki sposób ukierunkowane jest przyspieszenie?

Aby odpowiedzieć na powyższe pytanie, piszemy prędkość ciała w następującej formie:

v¯ = v * u _t ¯

Tutaj, u _t ¯ jest wektorem prędkości jednostkowej, indeks dolny t oznacza, że ​​jest skierowany stycznie do trajektorii (komponentu stycznego). Symbol v oznacza moduł prędkości v.

Teraz, zgodnie z definicją przyspieszenia, możemy rozróżnić prędkość względem czasu, mamy:

a¯ = dv¯ / dt = dv / dt * u _t ¯ + v * d (u _t ¯) / dt

Zatem całkowite przyspieszenie a¯ jest sumą wektorową dwóch składników. Pierwszy i drugi termin są nazywane przyspieszeniem punktu normalnego i stycznego. Przyjrzyj się bliżej każdemu z tych komponentów.

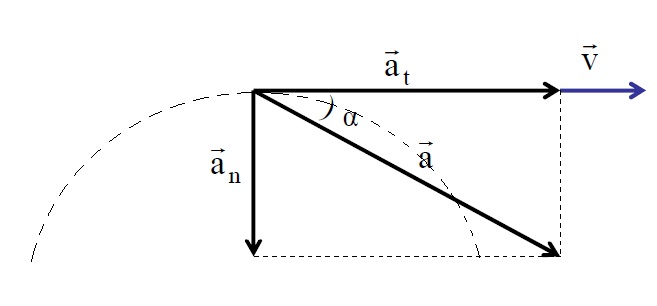
Przyspieszenie styczne

Piszemy raz jeszcze wzór dla tego składnika pełnego przyspieszenia:

a _t ¯ = dv / dt * u _t ¯

To wyrażenie pozwala nam opisać właściwości _t ¯:

• Jest on kierowany w taki sam sposób, jak prędkość sama w sobie lub przeciwnie do niej, to znaczy wzdłuż stycznej do trajektorii. Dowodem na to jest elementarny wektor u _t ¯.
• Charakteryzuje zmianę prędkości w wartości bezwzględnej, co odzwierciedla współczynnik dv / dt.

Te właściwości pozwalają nam wyciągnąć ważny wniosek: dla ruchu prostoliniowego pełne i styczne przyspieszenia mają tę samą wartość. W przypadku ruchu zakrzywionego całkowite przyspieszenie jest zawsze większe od wielkości stycznej. Rozważając fizyczne zadania prostoliniowego, równomiernie przyspieszonego ruchu, mówią o tym składniku przyspieszenia.

Przyspieszenie normalne

Biorąc pod uwagę szybkość, przyspieszenie styczne i przyspieszenie normalne, podajemy opis ostatniej wartości. Piszemy dla niego wzór:

a _n ¯ = v * d (u _t ¯) / dt = v * d (u _t ¯) / dL * dL / dt

Aby napisać wprost prawą stronę równości, używamy następujących relacji:

dL / dt = v;

d (u _t ¯) / dL = 1 / r

Tutaj dL jest odległością przebytą przez ciało w przedziale czasowym dt, r jest promieniem krzywizny trajektorii. Pierwsze wyrażenie odpowiada definicji prędkości, druga równość wynika z rozważań geometrycznych. Używając tych formuł, uzyskujemy końcowe wyrażenie dla normalnego przyspieszenia:

a _n ¯ = v ² / r

Oznacza to, że wartość _n ¯ nie zależy od zmiany prędkości, jako elementu stycznego, lecz zależy wyłącznie od jej modułu. Normalne przyspieszenie wzdłuż normalnej do tej części trajektorii jest kierowane, to znaczy w kierunku środka krzywizny. Na przykład, poruszając się po okręgu, wektor a _n ¯ jest kierowany do jego środka, dlatego normalne przyspieszenie jest często nazywane dośrodkowym.

Jeśli przyspieszenie jest styczne dla zmiany wielkości prędkości, wówczas normalny składnik jest odpowiedzialny za zmianę wektora prędkości, to znaczy określa trajektorię ciała.

Pełne, normalne i styczne przyspieszenie

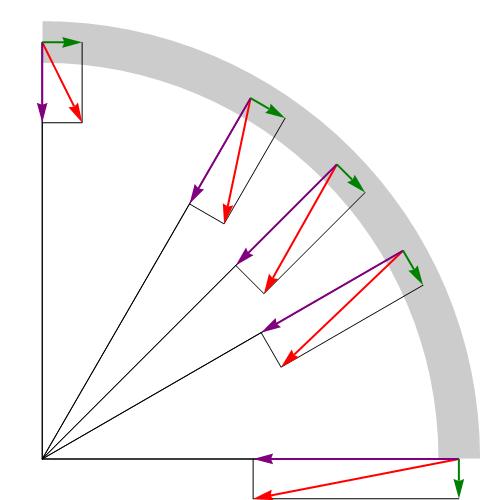
Po omówieniu pojęcia przyspieszenia i jego składników, podajemy teraz formułę, która pozwala nam określić pełne przyspieszenie. Ponieważ rozpatrywane komponenty są skierowane pod kątem 90 ^{o względem} siebie, twierdzenie Pitagorasa może być użyte do określenia wartości bezwzględnej ich sumy wektorowej. Wzór na pełne przyspieszenie to:

a = √ (a _t ² + a _n ² )

Kierunek wielkości a może być określony w odniesieniu do wektora dowolnego ze składników. Na przykład kąt między a¯ i _n ¯ jest obliczany jako:

θ = arctan (a _t / a _n )

Biorąc pod uwagę powyższą formułę dla modułu a, możemy wywnioskować: z równomiernym ruchem wzdłuż koła pełne przyspieszenie pokrywa się z dośrodkowym.

Rozwiązywanie problemów

Niech ciało porusza się w okręgu o promieniu 1 metra. Wiadomo, że jego prędkość zmienia się w zależności od następującego prawa:

v = 2 * t ² + 3 * t

Konieczne jest określenie przyspieszania stycznego i normalnego przyspieszenia w chwili t = 4 sekundy.

W przypadku stycznych mamy:

a _t = dv / dt = 4 * t + 3 = 19 m / s ²

Aby znaleźć normalny moduł przyspieszenia, należy najpierw obliczyć wartość prędkości w danym momencie. Mamy:

v = 2 * 4 ² + 3 * 4 = 44 m / s

Teraz możesz użyć formuły dla _n :

a _n = v ² / r = 44 ^2/1 = 1936 m / s ²

W ten sposób ustaliliśmy wszystkie ilości potrzebne do rozwiązania problemu.