Jak obliczyć procent ilości najprostszych sposobów

Każdego człowieka w jego życiu prawie codziennie spotyka się z pojęciem zainteresowania. Dotyczy to nie tylko uzyskania wartości procentowej z jednego numeru, ale także rozwiązania problemu, jak obliczyć procent sumy liczb. W życiu codziennym i codziennym wielu nie zwraca na to uwagi, niemniej jednak wszystkie te obliczenia są włączone do nas z ławki szkolnej.

Co to jest procent

Jeśli chodzi o pojęcie zainteresowania, można je wyjaśnić w najprostszy sposób, bez wchodzenia w podstawy obliczeń matematycznych. W rzeczywistości procent stanowi część czegoś innego. Nie ma znaczenia, w którym wskaźniku zostanie wyrażona zgodność procentowa do głównego źródła. Najważniejsze, aby zrozumieć, że taka reprezentacja może być w postaci samego procentu (%) lub w postaci ułamka, który ostatecznie określa stosunek części procentowej do pierwotnego wariantu.

Wykorzystanie zainteresowania w praktyce

Jak obliczyć odsetki, każdy z nas wie więcej ze szkolnego kursu matematyki. W życiu codziennym mamy do czynienia z wartościami procentowymi niemal co minutę. Każda gospodyni domowa, przygotowująca danie, używa przepisu, w którym procent jest prezentowany. Najprostszy przykład: weź pół szklanki mleka ... Jest to matematyczna interpretacja tego, co stanowi pewną część w stosunku do całości.

Zupełnie wszystkie obliczenia są oparte na 100 procentach (100%) lub jednym (1), jeśli obliczenia zostaną wykonane przy użyciu ułamków. Od tego i odpychany przy obliczaniu dowolnego składnika wskaźnika początkowego.

To samo dotyczy pytania, jak obliczyć procent kwoty, gdy początkowy (100 procent) wskaźnik nie jest jeden numer, ale kilka. Opcje obliczania tutaj mogą być całkiem sporo. Rozważ najbardziej podstawowe.

Oblicz procent według proporcji

Teraz nie będziemy brać pod uwagę obliczania odsetek za pomocą tych samych tabel programów biurowych, takich jak Excel, które robią to w trybie automatycznym podczas określania odpowiedniej formuły.

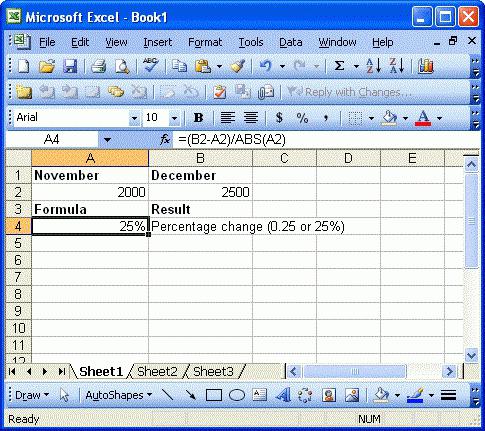
W niektórych przypadkach używany jest kalkulator, w którym można ustawić obliczanie takich działań. Ale teraz nie o to chodzi.

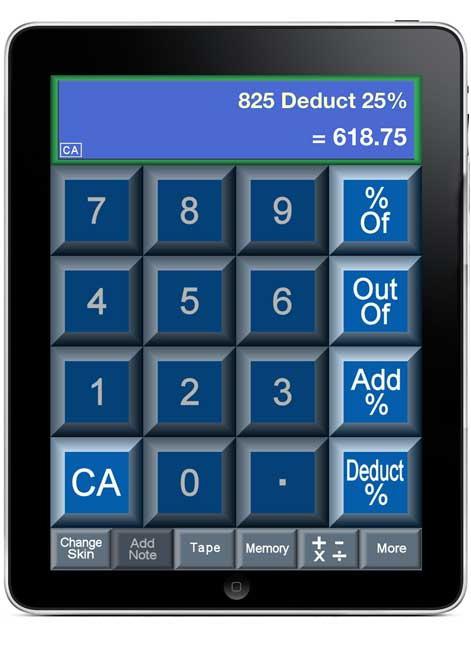
Rozważ najczęstsze metody obliczania, znane nam ze szkolnego kursu matematyki.

Najprostszym i najczęstszym sposobem jest rozwiązanie proporcji.

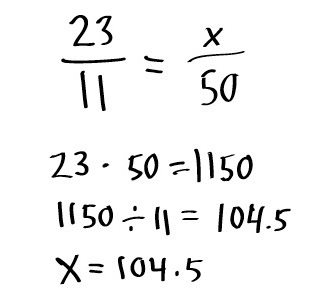
W tym przypadku początkowa liczba jest ustawiona jako 100 procent (powiedzmy, dowolna liczba "a"), a jej część (powiedzmy "b") - jako nieznane "x". W matematyce wygląda to tak:

a = 100%;

b = x.

W oparciu o zasady proporcji, możesz obliczyć nieznaną liczbę x. W tym celu stosuje się tak zwaną metodę krzyżową. Innymi słowy, musisz pomnożyć b przez 100 i podzielić przez a. Dokładnie ta sama zasada obowiązuje, jeśli w przypadku rysowania proporcji, zmieniaj b i x w miejscach, gdy procent jest znany, ale musisz obliczyć część w wyrażeniu liczbowym.

Szybkie obliczanie odsetek

Oczywiście naliczanie odsetek z pomocą proporcji jest podstawowa. Jednak przy użyciu liczb ułamkowych ta procedura jest uproszczona do niemożliwości. W końcu, co to jest w 50%? Połowa. To jest 1/2 lub 0,5 (w oparciu o początkową liczbę 1). Teraz jest jasne: aby obliczyć połowę, należy pomnożyć żądaną liczbę przez 1/2, lub 0,5, albo podzielić przez 2. Ta metoda jest jednak odpowiednia tylko dla liczb, które są podzielne bez reszty.

W przypadku znaków szczątkowych lub nieskończonych w okresie po przecinku, takich jak 0.33333333 ... lepiej jest używać wyrażeń ułamkowych, takich jak 1/3. Nawiasem mówiąc, ułamki (w niektórych przypadkach nieracjonalne) dokładnie odzwierciedlają samą liczbę, ponieważ okresowe cyfry po przecinku, bez względu na to, ile zadasz, nie dadzą liczby całkowitej. I tak ta sama jedna trzecia jasno i wyraźnie wyraża istotę.

W tych samych przepisach oczywiście jedna trzecia może być określona, ​​że ​​tak powiem, przez oko. Ale w procesach chemicznych, szczególnie tych związanych z drobnym dozowaniem składników, na przykład w przemyśle farmaceutycznym, ta metoda nie zadziała. Nie ma potrzeby polegać na oku. Konieczne jest stosowanie dokładnych stosunków składników, nawet jeśli jeden ze wskaźników ma postać liczby z liczbą w danym okresie lub jest reprezentowany w postaci tej samej nieracjonalnej frakcji. Ale, na przykład, przy ważeniu takie liczby mogą być ograniczone do kropki dziesiętnej po przecinku dziesiętnym lub maksymalnie jednej tysięcznej.

Jak obliczyć procent kwoty

Bardzo często trzeba radzić sobie z kilkoma wymaganymi liczbami lub ich sumą. Kwestia sposobu obliczania wartości procentowych kwoty jest rozwiązywana tak łatwo, jak w przypadku użycia pojedynczego numeru początkowego. Jedyną rzeczą do rozważenia w tym przypadku jest zwykła reprezentacja sumy jako pojedynczej wartości.

Na przykład mamy dwie liczby, aib, a początkowym wskaźnikiem jest liczba d. W takim przypadku proporcja będzie następująca:

d = 100%;

(a + b) = x.

Zauważ, że suma (a + b) może nadal być reprezentowana jako pojedyncza liczba. Niech to będzie z. W przypadku, gdy ustawimy formułę a + b = z, proporcja przyjmuje całkowicie standardową postać:

d = 100%;

z = x.

Jak widać, nic w tym skomplikowanego.

Istnieje inna opcja, gdy suma (a + b) = 100%, a d = x.

Oto rozwiązanie wygląda następująco:

(dx 100) / (a ​​+ b) lub (d / (a ​​+ b)) + 100 / (a ​​+ b).

Jak już wspomniano, stosuje się tutaj zasadę wspólnego mianownika dla ułamków.

Jeśli dodamy a i b, których suma jest równa z, proporcja znowu powraca do standardowej postaci:

z = 100%;

d = x.

To samo dotyczy odwrotnej kolejności.

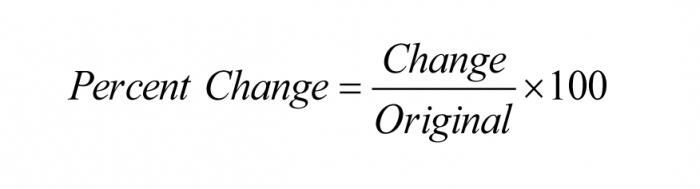
Matematyczne wyjaśnienie

Z punktu widzenia matematyki i jej podstaw, rozwiązanie problemu, w jaki sposób obliczyć procent kwoty, sprowadza się tylko do zastosowania najprostszych reguł rozszerzania nawiasów, gdy mnożymy sumę przez jedną liczbę i szukamy wspólnego mianownika, którym jest na ogół. Innymi słowy, można go przedstawić w następujący sposób:

ax (b + c) = ab + ac ,

gdzie ab i ac są produktami terminów w nawiasach (b i c) przez liczbę (współczynnik) przed nawiasami a.

W rzeczywistości ta sama metoda działa proporcjonalnie. Załóżmy, że mamy pewną liczbę z, reprezentującą 100%, oraz sumę liczb a i b. Procent do obliczenia jest oznaczony nieznaną liczbą y. W tym przykładzie wykonania proporcja przyjmuje postać:

z = 100%;

(a + b) = y.

Stąd proste rozwiązanie:

((a + b) x 100%) / z = ((ax 100%) + (bx 100%)) / z

W nawiasie podejmowane są działania mające na celu podkreślenie, że operacja mnożenia jest wykonywana w pierwszej kolejności, a dodawanie prac - w drugiej. Ta sama czynność jest wykonywana, jeśli początkowo suma liczb wynosi 100%.

Odwróć obliczenia

Bardzo często w kwestii sposobu obliczania procentu kwoty istnieje jednoznaczny zwrotny przelew. W praktyce wynika to, na przykład, z odwrotnego obliczenia kwartału. Wszyscy wiedzą, że ta liczba to 25% początkowej liczby. Niech, na przykład, cena towarów wzrosła o 25%, co wyniosło 25 rubli. Musimy dowiedzieć się, jak bardzo ten produkt się stał. Teraz postaramy się obliczyć, jak obliczyć nie początkową liczbę, znając wartość procentową, ale całą kwotę, która powinna się w końcu okazać. Wydaje się, że rozwiązanie jest proste:

25 = 25% (1/4 lub 0,25);

x = 100%.

Nie, absolutnie nie tak. Możesz uzyskać tylko początkowy numer, z wyłączeniem 25%. Aby obliczyć całą kwotę, biorąc pod uwagę 25% potrzeby użycia wzoru:

25 = 25%;

x = 100% + 25%.

Lub 100 / 0,8, które pokaże wartość 125 (100 + 25), ponieważ 100% plus 25% w wyrażeniu jednostkowym to liczba 1,25 (jedna plus jedna czwarta), a w odwrotności (1 / x) jest to tylko 0,8. Dokonując obliczeń otrzymamy x = 125.

Wniosek

Jak widać, nie ma nic szczególnie trudnego w obliczeniu procentu kwoty. To prawda, w programie szkolnym tłumaczenie zwrotne jest często pomijane z jakiegoś powodu. Wtedy wielu księgowych pracujących nad raportami płacącymi ten sam VAT często ma problemy.

Musisz więc wziąć pod uwagę podstawowe zasady obliczania odsetek, a problemy znikną same.

Z drugiej strony, dla wygody, zarówno proporcje jak i użycie frakcji mogą być stosowane w równym stopniu. W pierwszym przypadku mamy, by tak rzec, klasyczną wersję, w drugim - proste i uniwersalne rozwiązanie. Ponownie, lepiej jest użyć go w przypadku podziału bez reszty. Ale przy obliczaniu najpopularniejszych części, takich jak pół, ćwierć, trzeci itd., Ta metoda jest bardzo wygodna.

Obliczenia odwrotne, jak można zobaczyć na podstawie powyższych przykładów, również nie są złożone. Najważniejsze jest, aby wziąć pod uwagę współczynnik odwrotny przy obliczaniu pożądanej liczby. Wygląda na to, że teraz wszystko układa się na swoim miejscu. Jak mówią, prosta matematyka.