Jak zmniejszyć ułamek? Reguły dla wszystkich sytuacji
Bez wiedzy o tym, jak zmniejszyć ułamek i dostępność stabilnej umiejętności w rozwiązywaniu takich przykładów, bardzo trudno jest nauczyć się algebry w szkole. Im dalej, tym bardziej na podstawowej wiedzy na temat redukcji zwykłych frakcji nakładają się nowe informacje. Najpierw pojawiają się stopnie, potem mnożniki, które później stają się wielomiany.
Jak możesz się nie pogubić? Zasadniczo wzmacniaj umiejętności w poprzednich tematach i stopniowo przygotuj się na wiedzę o tym, jak redukować frakcje, które z roku na rok stają się coraz bardziej złożone.
Podstawowa wiedza
Bez nich nie będziesz w stanie poradzić sobie z zadaniami na żadnym poziomie. Aby to zrozumieć jak zmniejszyć ułamek trzeba zrozumieć dwa proste punkty. Po pierwsze: można tylko zmniejszyć czynniki. Ten niuans jest bardzo ważny, gdy wielomiany pojawiają się w liczniku lub mianowniku. Następnie musisz wyraźnie rozróżnić, gdzie znajduje się mnożnik i gdzie to określenie.
Drugi punkt sugeruje, że dowolną liczbę można przedstawić jako mnożniki. Co więcej, wynikiem redukcji jest taki ułamek, którego licznik i mianownik nie mogą być już zmniejszone.

Zasady redukcji zwykłych frakcji
Na początek warto sprawdzić, czy licznik jest podzielny przez mianownik lub odwrotnie. To na tej liczbie musisz dokonać redukcji. To jest najłatwiejsza opcja.
Druga to analiza pojawiania się liczb. Jeśli oba kończą się jednym lub więcej zerami, można je zmniejszyć o 10, 100 lub tysiąc. Tutaj możesz sprawdzić, czy liczby są równe. Jeśli tak, możesz bezpiecznie przeciąć dwa.
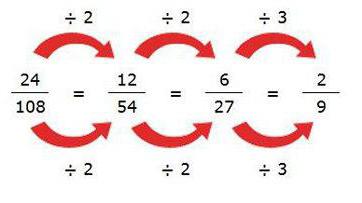
Trzecią zasadą zmniejszania frakcji staje się rozkład na czynniki pierwsze licznika i mianownika. W tym momencie musisz aktywnie wykorzystać całą wiedzę o znakach podzielności liczb. Po takim rozkładzie pozostaje tylko znaleźć wszystkie duplikaty, pomnożyć je i zmniejszyć o wynikową liczbę.
Co jeśli frakcja jest wyrażeniem algebraicznym?
Oto pierwsze trudności. Ponieważ to tutaj pojawiają się terminy, które mogą być identyczne z mnożnikami. Naprawdę chcą przeciąć, ale nie. Zanim zmniejszysz frakcję algebraiczną, musi ona zostać przekształcona tak, aby miała mnożniki.
Będzie to wymagało kilku kroków. Być może trzeba przejrzeć je wszystkie, a być może pierwsza z nich da odpowiednią opcję.
Sprawdź, czy licznik i mianownik lub dowolne wyrażenie w nich występuje różnią się znakiem. W takim przypadku wystarczy odjąć minus. Więc uzyskaj te same czynniki, które można zmniejszyć.
Sprawdź, czy wspólny czynnik można usunąć z wielomianu za pomocą nawiasów. Być może spowoduje to wspornik, który również może zostać skrócony, lub będzie renderowany jako monomialny.
Spróbuj zgrupować monomiony, aby później zrobić z nich wspólny czynnik. Potem może się okazać, że pojawią się mnożniki, które można zmniejszyć, lub ponownie powtórzyć usunięcie wspólnych elementów.
Spróbuj spojrzeć na skrócone formuły mnożenia w zapisie. Przy ich pomocy łatwo jest przekształcić wielomian w czynniki.
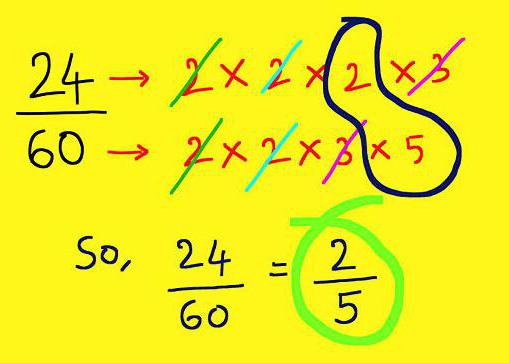
Sekwencja akcji z ułamkami ze stopniami
Aby łatwo zrozumieć kwestię redukcji ułamka za pomocą stopni, należy koniecznie dokładnie zapamiętać podstawowe działania z nimi. Pierwszy z nich jest związany z pomnażaniem mocy. W takim przypadku, jeśli podstawy są takie same, wskaźniki muszą być sumowane.
Drugi to podział. Ponownie, dla tych, którzy mają tę samą podstawę, wskaźniki będą musiały zostać odjęte. Musisz odjąć od liczby, która jest w dywidendach, a nie odwrotnie.
Trzeci to podniesienie do stopnia stopnia. W tej sytuacji wskaźniki są mnożone.
Skuteczna redukcja będzie również wymagać zdolności doprowadzania stopni do tej samej podstawy. To znaczy, aby zobaczyć, że cztery są dwa w kwadracie. Lub 27 - sześcian złożony z trzech. Ponieważ trudno jest przeciąć 9 w kwadracie i 3 w sześcianie. Ale jeśli konwertujesz pierwsze wyrażenie na (3 2 ) 2 , redukcja zakończy się pomyślnie.