Interpolacja to ... Definicja, cechy obliczeń i przykłady interpolacji

Wielu z nas miało do czynienia z niezrozumiałymi terminami w różnych naukach. Ale jest bardzo mało osób, które nie boją się niezrozumiałych słów, ale wręcz przeciwnie, zachęcają nas i zmuszają, by coraz więcej zgłębiać badany przedmiot. Dziś porozmawiamy o czymś takim jak interpolacja. Jest to metoda konstruowania wykresów ze znanych punktów, która pozwala, z minimalną ilością informacji o funkcji, przewidywać jej zachowanie na określonych odcinkach krzywej.

Zanim przejdziemy do istoty samej definicji i dokładniej ją opowiadamy, zagłębimy się nieco w tę historię.

Historia

Interpolacja jest znana od czasów starożytnych. Zjawisko to zawdzięcza jednak wielu znanym matematykom z przeszłości: Newtonowi, Leibnizowi i Grzegorzowi. Opracowali tę koncepcję za pomocą bardziej zaawansowanych metod matematycznych dostępnych w tym czasie. Wcześniej interpolacja była oczywiście używana i wykorzystywana w obliczeniach, ale została wykonana w całkowicie niedokładny sposób, który wymaga dużej ilości danych do zbudowania modelu, który jest mniej lub bardziej zbliżony do rzeczywistości.

Dziś możemy nawet wybrać, która metoda interpolacji jest bardziej odpowiednia. Wszystko zostało przetłumaczone na język komputerowy, który z dużą dokładnością może przewidzieć zachowanie funkcji w określonym obszarze, ograniczone znanymi punktami.

Interpolacja jest dość wąską koncepcją, dlatego jej historia nie jest tak bogata w fakty. W następnym rozdziale zrozumiemy, czym naprawdę jest interpolacja i czym różni się od jej przeciwieństwa - ekstrapolacją.

Czym jest interpolacja?

Jak już powiedzieliśmy, jest to ogólna nazwa sposobów budowania wykresu za punkty. W szkole odbywa się to głównie poprzez kompilację tabeli, identyfikację punktów na wykresie i z grubsza tworzenie linii łączących je. Ostatnia czynność jest podejmowana na podstawie rozważań o podobieństwie badanej funkcji do innych, rodzaju wykresów, które znamy.

Istnieją jednak inne, bardziej złożone i dokładne sposoby wykonania zadania kreślenia punktowego. Tak więc interpolacja jest faktycznie "prognozą" zachowania funkcji w określonym obszarze, ograniczoną znanymi punktami.

Istnieje podobna koncepcja związana z tym samym obszarem - ekstrapolacja. Przedstawia także prognozę wykresu funkcji, ale poza znanymi punktami wykresu. Przy pomocy tej metody przewidywanie jest dokonywane na podstawie zachowania funkcji w znanym przedziale, a następnie ta funkcja jest również stosowana do nieznanego przedziału. Ta metoda jest bardzo wygodna w praktycznym użyciu i jest aktywnie wykorzystywana, na przykład, w ekonomii do przewidywania wzrostów i spadków na rynku oraz do przewidywania sytuacji demograficznej w kraju.

Ale odeszliśmy od głównego tematu. W następnym rozdziale dowiemy się, jaki rodzaj interpolacji się dzieje i za pomocą których formuł można wykonać tę operację.

Rodzaje interpolacji

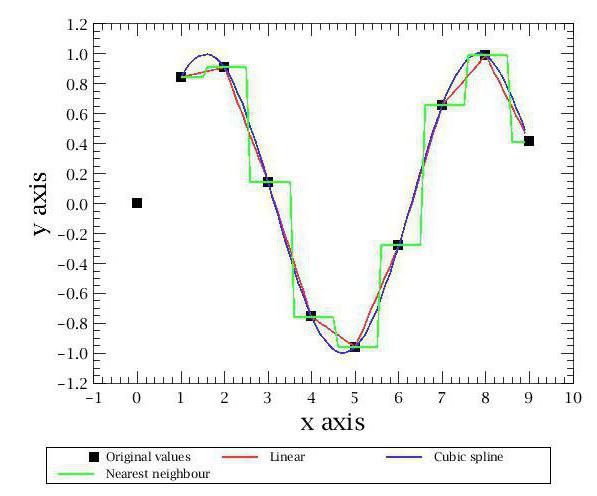
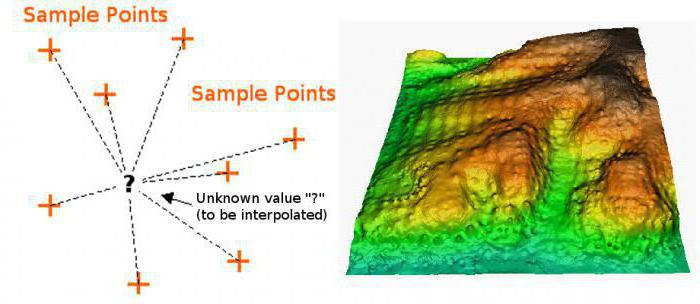
Najprostszym typem jest interpolacja najbliższego sąsiada. Dzięki tej metodzie otrzymujemy bardzo przybliżony wykres składający się z prostokątów. Jeśli widziałeś chociaż raz wyjaśnienie geometrycznego znaczenia całki na wykresie, to zrozumiesz, o jakiej formie graficznej mówimy.

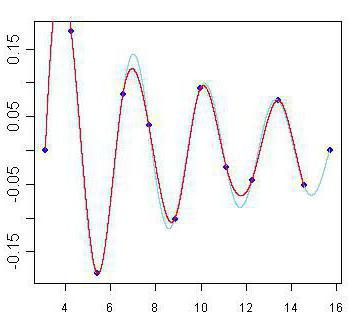
Ponadto istnieją inne metody interpolacji. Najbardziej znane i popularne są związane z wielomianami. Są bardziej dokładne i pozwalają przewidzieć zachowanie funkcji przy raczej słabym zestawie wartości. Pierwszą metodą interpolacji, którą rozważamy, będzie interpolacja liniowa za pomocą wielomianów. Jest to najprostszy sposób z tej kategorii iz pewnością każdy z was używał go w szkole. Jego istotą jest konstrukcja prostych linii między znanymi punktami. Jak wiadomo, pojedyncza prosta przechodzi przez dwa punkty płaszczyzny, których równanie można znaleźć na podstawie współrzędnych tych punktów. Tworząc te proste linie, otrzymujemy połamany wykres, który w jakiś sposób, ale odzwierciedla przybliżone wartości funkcji iw ogólnym ujęciu zbiega się z rzeczywistością. W ten sposób wykonywana jest interpolacja liniowa.

Skomplikowane typy interpolacji

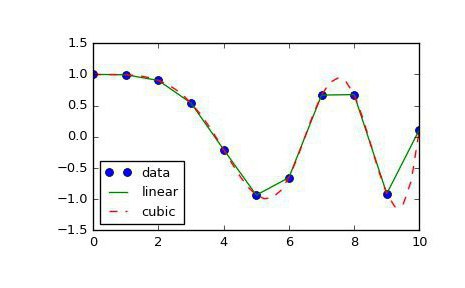
Istnieje bardziej interesująca, ale bardziej skomplikowana metoda interpolacji. Wynaleziony przez francuskiego matematyka Josepha Louisa Lagrange'a. Właśnie dlatego obliczenie interpolacji za pomocą tej metody nazwano od niego: interpolacja Lagrange'a. Skupiamy się na tym, że jeśli metoda opisana w poprzednim akapicie wykorzystuje do obliczeń jedynie funkcję liniową, wówczas dekompozycja Lagrange'a obejmuje również użycie wielomianów o wyższych stopniach. Ale nie jest łatwo znaleźć wzory interpolacji dla różnych funkcji. Im więcej punktów jest znanych, tym dokładniejsza jest formuła interpolacji. Ale istnieje wiele innych metod.

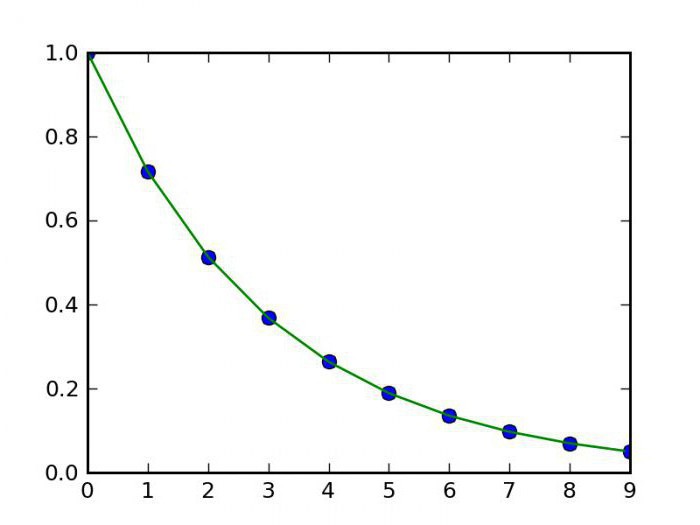
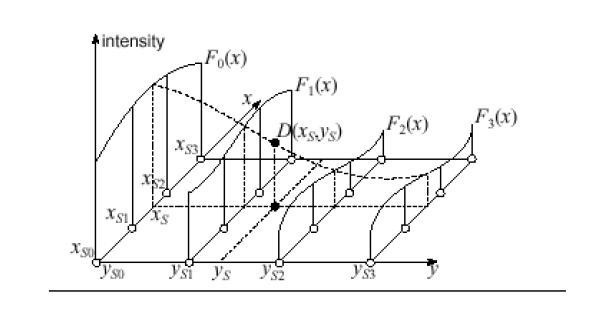
Istnieje również doskonała i realistyczna metoda obliczania. Zastosowana w nim formuła interpolacji jest zbiorem wielomianów, których zastosowanie zależy od obszaru funkcji. Ta metoda nazywa się funkcją splajnu. Ponadto istnieją również sposoby na przeprowadzenie takich funkcji, jak funkcje interpolujące dwóch zmiennych. Istnieją tylko dwie metody. Wśród nich podwójna lub podwójna interpolacja. Ta metoda pozwala łatwo budować wykres według punktów w trójwymiarowa przestrzeń. Inne metody nie będą miały wpływu. Ogólnie rzecz biorąc, interpolacja jest uniwersalną nazwą wszystkich tych metod graficznych, ale różnorodność sposobów wykonywania tego działania zmusza je do podziału na grupy w zależności od typu funkcji, która jest przedmiotem tego działania. Oznacza to, że interpolacja, której przykład rozważaliśmy powyżej, odnosi się do metod bezpośrednich. Istnieje również interpolacja odwrotna, która różni się tym, że pozwala nam obliczyć nie bezpośrednią, ale funkcję odwrotną (czyli x od y). Nie rozważymy najnowszych opcji, ponieważ jest to dość trudne i wymaga dobrej bazy wiedzy matematycznej.

Zwracamy się do jednej z najważniejszych sekcji. Z niej uczymy się, jak i gdzie stosuje się zestaw metod, o których mówimy w życiu.

Aplikacja

Matematyka jest znana jako królowa nauk. Dlatego też, nawet jeśli nie widzisz punktu w niektórych operacjach, nie oznacza to, że są one bezużyteczne. Na przykład wydaje się, że interpolacja jest rzeczą bezużyteczną, za pomocą której można zbudować tylko wykresy, których niewielu ludzi potrzebuje teraz. Jednak dla wszelkich obliczeń w inżynierii, fizyce i wielu innych naukach (na przykład biologii) niezwykle ważne jest zapewnienie dość kompletnego obrazu tego zjawiska, mając jednocześnie pewien zestaw wartości. Wartości rozproszone na wykresie nie zawsze dają jasny obraz zachowania funkcji w określonym obszarze, wartości jej pochodnych i punktów przecięcia z osiami. Jest to bardzo ważne w wielu dziedzinach naszego życia z tobą.

I jak to jest przydatne w życiu?

Na to pytanie bardzo trudno odpowiedzieć. Ale odpowiedź jest prosta: nie ma mowy. Ta wiedza nie będzie dla ciebie przydatna. Ale jeśli zrozumiesz ten materiał i metody, za pomocą których te działania zostaną wykonane, będziesz ćwiczyć swoją logikę, która jest bardzo przydatna w życiu. Najważniejsze nie jest sama wiedza, ale umiejętności, które osoba nabywa w procesie uczenia się. W końcu nic dziwnego, że jest takie powiedzenie: "żyj i ucz się".

Pojęcia pokrewne

Sam możesz zrozumieć, jak ważne (i wciąż nie tracisz na znaczeniu) ten obszar matematyki, patrząc na różnorodność innych pojęć z tym związanych. Mówiliśmy już o ekstrapolacji, ale jest też przybliżenie. Może już słyszałeś to słowo. W każdym razie, co to oznacza, omówiliśmy również w tym artykule. Aproksymacja, podobnie jak interpolacja, jest pojęciem związanym z budową wykresów funkcji. Ale różnica między pierwszym a drugim polega na tym, że przedstawia przybliżoną konstrukcję wykresu opartego na podobnych znanych wykresach. Te dwa pojęcia są do siebie bardzo podobne i bardziej interesujące jest zbadanie każdego z nich.

Wniosek

Matematyka nie jest tak skomplikowaną nauką, jak się wydaje na pierwszy rzut oka. To raczej interesujące. W tym artykule próbowaliśmy ci to udowodnić. Przejrzeliśmy koncepcje związane z budową wykresów, dowiedzieliśmy się, czym jest podwójna interpolacja i rozmontowujemy ją z przykładami, w których jest używana.