Pomiar współczynnika załamania światła szkła. Prace laboratoryjne

Znajomość współczynnika załamania światła danego szkła jest ważna dla jego zastosowania jako materiału na soczewki optyczne. W tym artykule przedstawiamy prace laboratoryjne dotyczące pomiaru współczynnika załamania światła szkła, uwzględniając wszystkie niezbędne formuły po drodze.

Cel i cele pracy laboratoryjnej

Laboratoryjny pomiar współczynnika załamania światła szkła ma na celu osiągnięcie następującego celu: nauczyć się mierzyć charakterystykę refrakcyjną przezroczystych materiałów i przetwarzać wyniki.

W trakcie pracy należy rozwiązać następujące zadania:

• Aby studiować materiał teoretyczny.
• Przestudiuj eksperymentalny układ i jego zasadę działania.
• Aby obliczyć kąty padania i załamania.
• Określ kąt krytyczny.
• Znajdź wartość współczynnika załamania dla szkła, przetwarzając wyniki.
• Wyciągnij wnioski na temat pracy.

Teoria zjawiska refrakcji

Zjawisko to polega na zmianie kierunku prostoliniowego ruchu wiązki światła, gdy przemieszcza się ona od jednego przezroczystego medium do drugiego. Taka sytuacja powstaje, na przykład, gdy światło przekracza granicę wody - powietrze lub szkło - powietrze.

Prawa refrakcji interesowały ludzkość w całej jej historii. Zajmowali się starożytnymi Grekami (Ptolemeusz, I-II wne), Arabami w średniowieczu (Ibn Sahl, X wiek), a także wieloma naukowcami w nowym czasie (Huygens, Newton, Descartes, Snell). Obecnie uważa się, że Holender Snell po raz pierwszy sformułował prawo refrakcji w nowoczesnej formie, podsumowując wiele danych eksperymentalnych.

Wzór na zjawisko załamania ma następującą postać:

n ₁ * sin (θ ₁ ) = n ₂ * sin (θ ₂ ) = const.

Tutaj θ ₁ jest kątem w stosunku do normalnego do granicy między ośrodkiem, w którym wiązka uderza w tę powierzchnię, θ ₂ jest kątem w stosunku do tej samej wartości normalnej dla załamanego promienia. Wartości n ₁ , n ₂ są odpowiednio współczynnikami załamania dla mediów 1 i 2. Wskaźnik n określa, jak mocno medium spowalnia prędkość światła w stosunku do prędkości w próżni, czyli:

n = c / v, c jest prędkością światła w próżni, v znajduje się w ośrodku.

Kąt krytyczny

Prawo Snell'a wykazuje, że kąt padania jest większy niż kąt załamania, jeśli pierwsza warstwa jest optycznie mniej gęsta (n ₁₎ 2). Odwrotność też jest prawdą.

Kiedy wiązka porusza się w optycznie bardziej gęstym ośrodku i przechodzi przez powierzchnię pośrednią między mediami w mniej gęstą przezroczystą substancję, wtedy występuje kąt, w którym załamująca się wiązka porusza się wzdłuż powierzchni oddzielającej ośrodek. Ten kąt jest krytyczny. Wszelkie kąty padania, które są większe niż to, doprowadzą do tego, że żadna część światła nie przechodzi przez interfejs. Zjawisko to nazywane jest wewnętrzną pełną refleksją.

Biorąc pod uwagę prawo Snella i powyższe wyjaśnienia, pod kątem krytycznym możesz napisać:

θ ₁ = arcsin (n ₂ / n ₁ ), gdzie n ₁ > n ₂ .

Zjawisko to jest używane w światłowodach do przesyłania energii elektromagnetycznej na duże odległości bez strat.

Konfiguracja eksperymentalna

Wyznaczenie współczynnika załamania światła szkła wykonuje się za pomocą instalacji, co pokazano na poniższym rysunku.

Liczby na zdjęciu oznaczają:

1. Linia stopniowana, na której znajdują się główne urządzenia robocze instalacji.
2. Źródło energii elektrycznej.
3. Lampa, która jest źródłem światła.
4. Soczewka zbierająca o znanej długości ogniskowej (na przykład 10 cm).
5. Kaseta do przepon.
6. Przysłona w postaci kraty (otwory służą do lepszego skupienia wiązki światła).
7. Optyczny dysk z podziałką.
8. Obiekt szklany, którego współczynnik załamania powinien być mierzony. Ma on kształt półcylindra, tzn. Jego trzy powierzchnie to płaszczyzny, a czwarta jest cylindryczna.
9. Pryzmat optyczny (nieużywany w tej pracy laboratoryjnej).

Dlaczego konieczne jest użycie szklanego przedmiotu w postaci półcylindra, zostanie wyjaśnione poniżej.

Przygotowanie instalacji do działania

Zasada działania instalacji do eksperymentalnego pomiaru współczynnika załamania światła szkła jest niezwykle prosta: konieczne jest jedynie utworzenie wąskiej wiązki światła, przesłanie jej równolegle do tarczy optycznej przez szklany półcylindryczny, a za pomocą podziałki dysku zmierzyć kąt padania i kąt załamania.

Przygotowanie do instalacji odbywa się sekwencyjnie:

1. Umieść źródło światła (lampę) na podziałce liniowej w pozycji "0 cm".
2. Umieść ciało soczewką zbierającą na miarce podziałki w pozycji równej ogniskowej. W tym przypadku 10 cm. Z powodu tej pozycji wszystkie promienie emitowane przez obiektyw będą wygaszać równolegle do podziałki liniowej.
3. Włącz źródło zasilania i, regulując położenie membran, upewnij się, że wiązka światła jest tak wąska, jak to możliwe. Jego grubość powinna być znacznie mniejsza niż najmniejszy podział na dysku optycznym.
4. Dostosuj wysokość położenia dysku optycznego tak, aby wiązka światła przechodziła nad nią, prawie dotykając jej powierzchni. Dysk powinien również być ustawiony względem osi bocznej tak, aby wiązka przechodziła dokładnie przez jej środek, czyli przez jedną ze średnic.
5. W środku tarczy należy umieścić szklany półcylindr, tak aby jego płaszczyzna boczna pokrywała się z jedną ze średnic tarczy.

Konfiguracja jest gotowa na eksperyment.

Przeprowadzanie eksperymentu

Praca laboratorium "Pomiar współczynnika refrakcji szkła" składa się z dwóch etapów. Najpierw przeprowadź eksperyment, aby przenieść wiązkę światła z powietrza na szkło, a następnie ze szkła na powietrze:

• Od powietrza do szkła. Najpierw należy obrócić dysk optyczny tak, aby po przejściu przez półcylinder belka nie załamała się. Ta pozycja będzie odpowiadać pochodzeniu (0 ^o ). Następnie należy obrócić dysk na każde 5 ^o i wprowadzić dane do odpowiedniej tabeli: α i β - kąty padania i załamania. Konieczne jest przeprowadzenie około 10-15 pomiarów. Położenie półcylindra na dysku można zobaczyć na poniższym rysunku (a).
• Od szkła do powietrza. W takim przypadku tarcza z półcylindrem powinna być obrócona ^o 180 °. W takim przypadku wiązka padająca najpierw wpadnie na cylindryczną powierzchnię. Ponieważ pada na niego wzdłuż promienia (pod kątem 90 ^o ), nie dochodzi do załamania przy wejściu do szkła i występuje tylko przy wyjściu z niego przez płaską powierzchnię. Ta sytuacja została przedstawiona na rysunku poniżej (b). Wybierając punkt odniesienia jak w powyższym przypadku, należy obracać dysk co 5 ^o i mierzyć kąty.

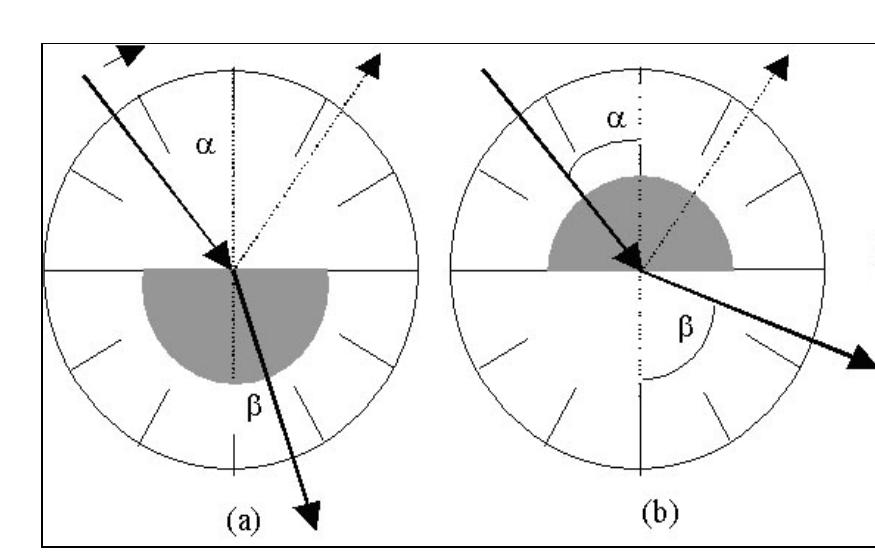
Kiedy wykonywane jest doświadczenie "szkło-powietrze", powstaje sytuacja pod pewnym kątem padania wiązki, gdy nie wychodzi ona przez płaską powierzchnię półcylindra. Ten kąt jest krytyczny.

Przetwarzanie wyników

Dla każdej pary kątów α i β oblicz wartość n _i dla szkła. Odbywa się to za pomocą wzorów do pomiaru współczynnika refrakcji szkła. Rozwiązanie z prawa Snell'a jest następujące:

• Od powietrza do szkła: n _i = _nv * sin (α) / sin (β).
• Od szkła do powietrza: n _i = _nv * sin (β) / sin (α).

Współczynnik załamania światła powietrza wynosi n _v = 100029.

W ten sposób otrzymujemy serię wartości n (ich liczba jest równa całkowitej liczbie wykonanych pomiarów). Niech ta liczba będzie m. Teraz należy znaleźć średnią wartość współczynnika refrakcji szkła n¯, a także wariancję Δn (średnie odchylenie kwadratu), pokazującą dokładność eksperymentu. Wartości te są określane przez następujące formuły:

n¯ = Σ _{i = 1} ^m (n _i ) / m;

Δn = √ (Σ _{i = 1} ^m (ni _- n¯) ² / m).

Wynik końcowy jest zapisany w formie:

n¯ ± Δn.

Wnioski dotyczące pracy w laboratorium

Po wykonaniu pracy "Pomiar współczynnika załamania szkła", wnioski można wyciągnąć w następujący sposób:

• promień światła ulega załamaniu po przejściu na inny nośnik;
• kąt krytyczny powstaje tylko w przypadku przejścia światła ze szkła na powietrze, ale nie na odwrót;
• dla wiarygodności uzyskanego wyniku należy wykonać kilka pomiarów (więcej niż 10), a następnie wartość końcową należy przedstawić jako wartość średnią, wskazując granicę jej dokładności.