Równoległościan: podstawowe formuły i przykłady zadań
Często uczniowie z oburzeniem pytają: "Jak mogę tego użyć w życiu?" Na każdy temat każdego przedmiotu. Kwestia wolumenu równoległościanu nie jest wyjątkiem. A tutaj możesz po prostu powiedzieć: "To jest przydatne".
Jak na przykład sprawdzić, czy opakowanie zmieści się w skrzynce pocztowej? Oczywiście, za pomocą prób i błędów można wybrać odpowiedni. A jeśli nie ma takiej możliwości? Na ratunek przychodzą obliczenia. Znając pojemność pudełka, możesz obliczyć objętość paczki (przynajmniej w przybliżeniu) i odpowiedzieć na postawione pytanie.
Równoległościany i jego typy
Jeśli dosłownie przetłumaczysz jego nazwę na starożytną grekę, okazuje się, że jest to postać składająca się z równoległych płaszczyzn. Istnieją równoważne definicje równoległościanu:
- pryzmat z podstawą w postaci równoległoboku;
- wielościan, którego każda powierzchnia jest równoległobokiem.
Jego rodzaje wyróżniają się w zależności od tego, która postać leży u podstawy i jak skierowane są krawędzie boczne. Mówią ogólnie o nachylonym równoległościanie , którego podstawa i wszystkie powierzchnie są równoległobokami. Jeśli w poprzednim widoku, powierzchnie boczne staną się prostokątami, wówczas będą musiały zostać nazwane liniami prostymi . A prostokątna podstawa ma również kąty 90 °.
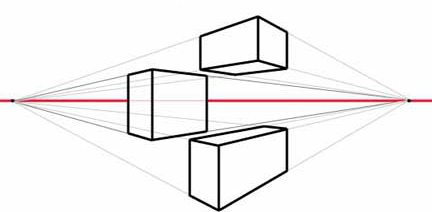
A te ostatnie w geometrii starają się przedstawić tak, aby zauważyć, że wszystkie krawędzie są równoległe. Tu nawiasem mówiąc, zaobserwowano zasadniczą różnicę między matematykami i artystami. Na koniec ważne jest, aby przenieść ciało zgodnie z prawem perspektywy. I w tym przypadku równoległość żeber jest całkowicie niewidoczna.
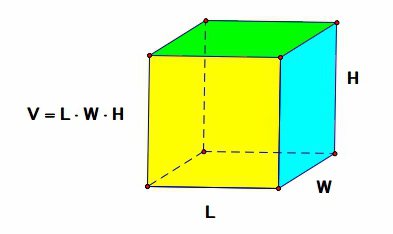
Informacje o wprowadzonej notacji
W poniższych wzorach notacja w tabeli jest poprawna.
| Wielkość | Jego oznaczenie |
| podstawowe długości krawędzi | a |
| boczna długość żebra | z |
| wysokość | n |
| obszar bazowy | S o |
| powierzchnia boczna | S b |
| całkowita powierzchnia | S p |
| obwód podstawy | R o |
| Tom | V |
Formuły dla ukośnego równoległościanu
Pierwszy i drugi dla przestrzeni:
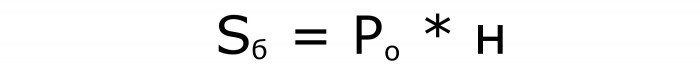
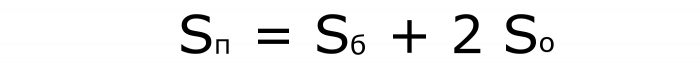
Trzeci w celu obliczenia objętości równoległościanu:

Ponieważ podstawą jest równoległobok, a następnie do obliczenia jego powierzchni, będziesz musiał użyć odpowiednich wyrażeń.
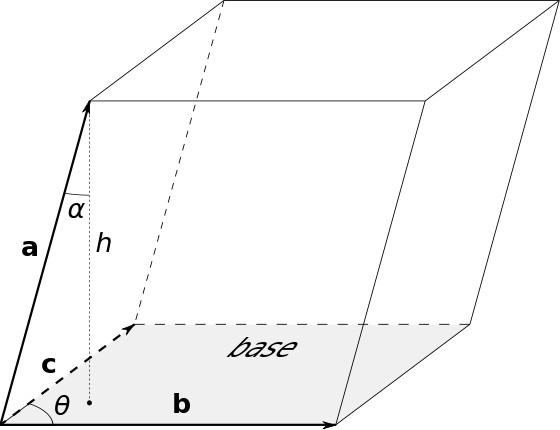
Wzory na prostokątny równoległościan
Podobnie do pierwszego elementu - dwie formuły dla obszarów:
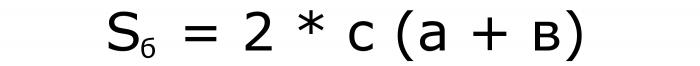
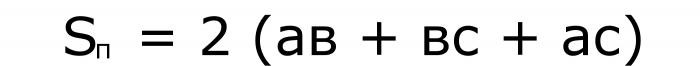
I jeszcze jeden na tom:

Pierwsze zadanie
Stan Biorąc pod uwagę prostokątny równoległościan, którego objętość chcesz znaleźć. Znana przekątna - 18 cm - i fakt, że tworzy on kąty 30 i 45 stopni, odpowiednio z płaszczyzną bocznej ściany i bocznej krawędzi.
Decyzja. Aby odpowiedzieć na pytanie o problem, musisz znać wszystkie strony w trzech prawe trójkąty. Podadzą niezbędne wartości krawędzi, które należy policzyć.
Najpierw musisz się dowiedzieć, gdzie kąt wynosi 30º. Aby to zrobić, należy narysować przekątną powierzchni bocznej z tego samego wierzchołka, z którego została wyciągnięta główna przekątna równoległoboku. Kąt między nimi będzie tym, co jest potrzebne.
Pierwszy trójkąt, który da jedną z wartości boków podstawy, będzie następny. Zawiera pożądaną stronę i dwie ułożone ukośnie. Jest prostokątny. Teraz musisz użyć stosunku po przeciwnej stronie (strona bazowa) i przeciwprostokątnej (przekątnej). Jest równy sinusowi 30º. Oznacza to, że nieznana strona podstawy zostanie określona jako przekątna pomnożona przez sinus 30º lub ½. Niech będzie oznaczone literą "a".
Łatwo zliczyć: a = 18 * ½ = 9 (cm).
Drugi będzie trójkątem zawierającym znaną przekątną i krawędzią, z którą tworzy 45º. Jest również prostokątny i można ponownie użyć relacji nogi do przeciwprostokątnej. Innymi słowy, krawędź boczna do przekątnej. Jest równy cosinusowi 45º. Oznacza to, że "c" jest obliczane jako iloczyn przekątnej przez cosinus wynoszący 45º.
c = 18 * 1 / √2 = 9 √ 2 (cm).
W tym samym trójkącie wymagane jest znalezienie innej nogi. Jest to konieczne, aby zliczyć trzecie nieznane - "w". Niech to będzie oznaczone literą "x". Łatwo obliczyć za pomocą twierdzenia Pitagorasa:
x = √ (18 2 - (9√2) 2 ) = 9√2 (cm).
Teraz musimy wziąć pod uwagę kolejny trójkąt prostokątny. Zawiera już znane strony "s", "x" i ten, który musisz liczyć, "c":
c = √ ((9√2) 2 - 9 2 = 9 (cm).
Wszystkie trzy wielkości są znane. Możesz użyć formuły dla woluminu i policzyć ją:
V = 9 * 9 * 9 2 = 729 x 2 (cm 3 ).
Odpowiedź: objętość równoległościanu wynosi 729 × 2 cm 3 .
Drugie zadanie
Stan Wymagane jest znalezienie objętości równoległościanu. Znane są boki równoległoboku, który leży u podstawy, 3 i 6 cm, a także jego kąt ostry - 45º. Krawędź boczna ma nachylenie do podstawy 30º i ma 4 cm.
Decyzja. Aby odpowiedzieć na pytanie o problem, musisz przyjąć formułę, która została napisana dla woluminu pochylonego równoległościanu. Ale obie wielkości nie są w nim znane.
Obszar podstawy, czyli równoległobok, będzie określony przez wzór, w którym należy pomnożyć znane boki i sinus kąta ostrego między nimi.
S о = 3 * 6 sin 45º = 18 * (√2) / 2 = 9 √ 2 (cm 2 ).
Drugą nieznaną jest wysokość. Można go narysować z dowolnego z czterech wierzchołków nad podstawą. Można go znaleźć z trójkąta prostokątnego, w którym wysokość jest nogą, a krawędź boczna to przeciwprostokątna. Kąt 30º leży naprzeciwko nieznanej wysokości. Możesz więc użyć postawy nogi do przeciwprostokątnej.
n = 4 * sin 30º = 4 * 1/2 = 2.
Teraz wszystkie wartości są znane i możesz obliczyć objętość:
V = 9 √ 2 * 2 = 18 √ 2 (cm 3 ).
Odpowiedź: objętość wynosi 18 √ 2 cm 3 .
Trzecie zadanie
Stan Znajdź objętość równoległościanu, jeśli wiesz, że jest prosty. Boki jego podstawy tworzą równoległobok i mają 2 i 3 cm, a kąt ostry między nimi wynosi 60 °. Mniejsza przekątna równoległościanu jest równa większej przekątnej podstawy.
Decyzja. Aby sprawdzić objętość równoległościanu, używamy wzoru z powierzchnią bazową i wysokością. Obie wielkości są nieznane, ale nie są trudne do obliczenia. Pierwszy to wzrost.
Ponieważ mniejsza przekątna równoległościanu pokrywa się rozmiar z większe podstawy, można je wyznaczyć jedną literą d. Większy kąt równoległoboku wynosi 120 °, ponieważ tworzy 180 ° ostrą. Niech druga przekątna podstawy będzie oznaczona literą "x". Teraz można zapisać dwie przekątne podstawy twierdzenia cosinusowe :
d 2 = a 2 + in 2 - 2av cos 120º,
x 2 = a 2 + in 2 - 2av cos 60º.
Szukanie wartości bez kwadratów nie ma sensu, ponieważ wtedy znów zostaną podniesione do drugiej potęgi. Po uzyskaniu substytucji danych:
d 2 = 2 2 + 3 2 - 2 * 2 * 3 cos 120º = 4 + 9 + 12 * ½ = 19,
x 2 = a 2 + in 2 - 2av cos 60º = 4 + 9 - 12 * ½ = 7.
Teraz wysokość, która jest boczną krawędzią równoległościanu, będzie nogą w trójkącie. Przeciwprostokątna będzie znaną przekątną ciała, a druga noga będzie "x". Możesz napisać twierdzenie Pitagorasa:
n 2 = d 2 - x 2 = 19 - 7 = 12.
Stąd: n = √12 = 2√3 (cm).
Teraz druga nieznana ilość to powierzchnia podstawy. Można to zliczyć za pomocą wzoru wymienionego w drugim problemie.
S = = 2 * 3 sin 60º = 6 * √3 / 2 = 3√3 (cm 2 ).
Łącząc wszystko w formule objętości, otrzymujemy:
V = 3√3 * 2√3 = 18 (cm 3 ).
Odpowiedź: V = 18 cm 3 .

Czwarte zadanie
Stan Wymagana jest znajomość objętości równoległościanu, który spełnia te warunki: podstawa - kwadrat o boku 5 cm; powierzchnie boczne są rombowe; jeden z wierzchołków nad podstawą jest w równej odległości od wszystkich wierzchołków u podstawy.
Decyzja. Najpierw musisz poradzić sobie z tym stanem. W pierwszym akapicie o kwadracie nie ma pytań. Drugi, dotyczący rombów, wyjaśnia, że równoległościan jest nachylony. Co więcej, wszystkie jego krawędzie mają 5 cm, ponieważ boki rombu są takie same. A z trzeciego staje się jasne, że trzy przekątne z niego wyprowadzone są równe. Są to dwa, które leżą na bocznych ścianach, a drugie są wewnątrz równoległościanu. A te przekątne są równe krawędzi, to znaczy mają również długość 5 cm.
Aby określić objętość, potrzebna będzie formuła napisana dla nachylonego równoległościanu. Ponownie nie ma znanych wartości. Jednak obszar podstawy jest łatwy do obliczenia, ponieważ jest kwadratowy.
S o = 5 2 = 25 (cm 2 ).
Trochę trudniej jest z wysokością. Będzie to takie na trzech figurach: równoległościan, czworokątna piramida i trójkąt równoramienny. Ostatnia okoliczność i potrzeba skorzystania.
Ponieważ jest to wysokość, jest to noga w trójkącie prostokątnym. Przeciwprostokątna będzie znaną krawędzią, a druga noga równa się połowie przekątnej kwadratu (wysokość jest również medianą). A przekątna podstawy jest łatwa do znalezienia:
d = √ (2 * 5 2 ) = 5√2 (cm).
Konieczne będzie policzenie wysokości jako różnicy drugiego stopnia krawędzi i kwadratu połowy przekątnej i pamiętaj, aby wyodrębnić pierwiastek kwadratowy :
n = √ (5 2 - (5/2 * √2) 2 ) = √ (25 - 25/2) = √ (25/2) = 2,5 √ 2 (cm).
Pozostaje policzyć objętość:
V = 25 * 2,5 √ 2 = 62,5 √ 2 (cm 3 ).
Odpowiedź: 62,5 √ 2 (cm 3 ).