Równania kwadratowe. Rozwiązywanie równań kwadratowych
Na początku ten temat może wydawać się skomplikowany z powodu wielu niezbyt prostych formuł. Równoległe równania kwadratowe mają nie tylko długie pozycje, ale także korzenie można znaleźć przez dyskryminator. Istnieje w sumie trzy nowe formuły. Niezbyt łatwe do zapamiętania. Jest to możliwe dopiero po częstym rozwiązywaniu takich równań. Wtedy wszystkie wzory zostaną zapamiętane osobno.

Widok ogólny równania kwadratowego
Tutaj oferowane są wyraźne zapisy, kiedy największy stopień jest zapisywany jako pierwszy, a następnie - w porządku malejącym. Często zdarzają się sytuacje, gdy komponenty są ze sobą w sprzeczności. Wtedy lepiej jest przepisać równanie w porządku malejącym stopnia zmiennej.
Wprowadzamy notację. Zostały one przedstawione w poniższej tabeli.
| Oznaczenie wielkości | Jej imię |
| a, b, c | współczynniki, które są liczbami arbitralnymi |
| x | zmienna |
| D | dyskryminujący |
| x 1 x 2 | korzenie równania |
Jeśli przyjmiemy te oznaczenia, wszystkie równania kwadratowe zmniejszą się do następującego wpisu.
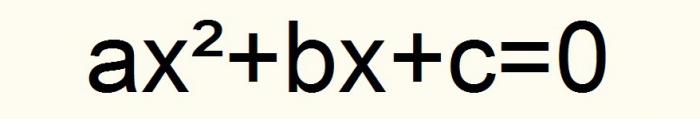
Co więcej, współczynnik a ≠ 0. Niech ta formuła będzie oznaczona numerem jeden.
Kiedy podane jest równanie, nie jest jasne, ile korzeni znajdzie się w odpowiedzi. Ponieważ jedna z trzech opcji jest zawsze możliwa:
- rozwiązanie będzie miało dwa korzenie;
- odpowiedź to jeden numer;
- korzenie równania nie będą w ogóle.
I choć decyzja nie została zakończona, trudno jest zrozumieć, która z opcji będzie dotyczyła konkretnej sprawy.
Rodzaje zapisów równań kwadratowych
W zadaniach mogą znajdować się różne wpisy. Nie zawsze będą one wyglądały jak ogólna formuła równania kwadratowego. Czasami będzie tęsknić za niektórymi przedmiotami. To, co zostało napisane powyżej, jest pełnym równaniem. Jeśli usuniesz drugi lub trzeci termin, otrzymasz coś innego. Te zapisy są również nazywane równaniami kwadratowymi, tylko niekompletne.
Co więcej, tylko terminy, których współczynniki są "in" i "c" mogą zniknąć. Liczba "a" nie może wynosić zero w żadnych warunkach. Ponieważ w tym przypadku formuła zamienia się w równanie liniowe. Formuły dla niekompletnej postaci równań są następujące:
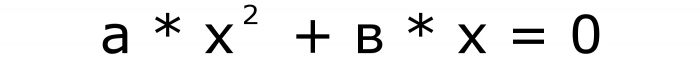
i
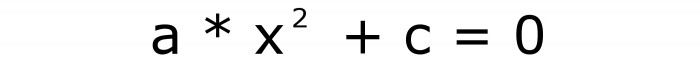
Istnieją więc tylko dwa typy, oprócz pełnych, istnieją również niepełne równania kwadratowe. Niech pierwsza formuła będzie numerem dwa, a druga trójką.
Dyskryminacja i zależność liczby korzeni od jej wartości
Musisz znać ten numer, aby obliczyć korzenie równania. Zawsze można go obliczyć, niezależnie od wzoru równania kwadratowego. Aby obliczyć dyskryminatora, musisz użyć równania opisanego poniżej, które będzie miało numer cztery.

Po podstawieniu wartości współczynników w tym wzorze można uzyskać liczby z różnymi znakami. Jeśli odpowiedź brzmi tak, to odpowiedź na równanie będzie dwiema różnymi korzeniami. Przy liczbie ujemnej korzenie równania kwadratowego będą nieobecne. W przypadku równości do zera odpowiedź będzie jedna.
W jaki sposób rozwiązano kwadratowe równanie kompletnej formy?
W rzeczywistości rozważanie tej kwestii już się rozpoczęło. Ponieważ najpierw musisz znaleźć dyskryminatora. Gdy już okaże się, że istnieją korzenie równania kwadratowego, a ich liczba jest znana, konieczne jest użycie formuł dla zmiennych. Jeśli istnieją dwa pierwiastki, musisz zastosować tę formułę.
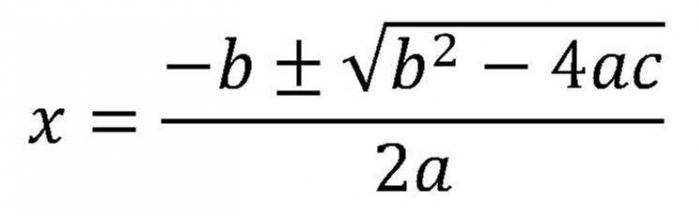
Ponieważ jest w nim znak "±", będą dwie wartości. Wyrażenie pierwiastka kwadratowego jest wyróżnikiem. Dlatego formułę można inaczej napisać.
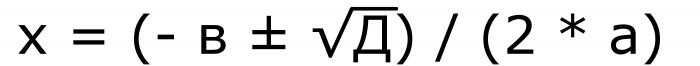
Formuła piątej. Z tego samego rekordu jasne jest, że jeśli wyróżnik wynosi zero, to oba korzenie przyjmą te same wartości.
Jeśli rozwiązanie równań kwadratowych nie zostało jeszcze wypracowane, lepiej jest zapisać wartości wszystkich współczynników przed zastosowaniem formuł dyskryminacyjnych i zmiennych. Później ten moment nie sprawi trudności. Ale na samym początku jest zamieszanie.
W jaki sposób rozwiązano kwadratowe równanie niepełne?
Tutaj wszystko jest o wiele prostsze. Nawet nie ma potrzeby stosowania dodatkowych formuł. I nie potrzebujesz tych, które zostały już nagrane dla osoby dyskryminującej i nieznanej.
Najpierw rozważamy niepełne równanie numer dwa. W tej równości zakłada się, że odstawia się nieznaną wartość ze wspornika i rozwiązuje równanie liniowe, które pozostanie w nawiasach. Odpowiedź będzie dwiema korzeniami. Pierwszy jest koniecznie równy zeru, ponieważ istnieje czynnik składający się z samej zmiennej. Drugi okaże się na decyzję równanie liniowe.
Niepełne równanie numer trzy rozwiązuje się, przenosząc liczbę z lewej strony równości w prawo. Następnie musisz podzielić przez współczynnik twarzą w twarz z nieznanym. Pozostaje tylko wyodrębnić pierwiastek kwadratowy i pamiętaj, aby zapisać go dwukrotnie z przeciwnymi znakami.

Przydatne wskazówki
Ponadto, rejestrowane są niektóre działania, które pomagają nauczyć się rozwiązywać wszystkie rodzaje równości, które zamieniają się w równania kwadratowe. Pomogą one uczniowi uniknąć nieuważnych błędów. Te niedociągnięcia są przyczyną złych szacunków w badaniu obszernego tematu "Równania kwadratowe (klasa 8)". Następnie działania te nie będą musiały stale wykonywać. Ponieważ nie będzie stałej umiejętności.
- Najpierw musisz napisać równanie w standardowej formie. To znaczy najpierw określenie o największym stopniu zmiennej, a następnie - bez stopnia i ostatniego - tylko liczba.
- Jeśli przed współczynnikiem "a" pojawi się minus, to może skomplikować pracę dla początkującego, aby studiować równania kwadratowe. Lepiej się go pozbyć. W tym celu cała równość musi być pomnożona przez "-1". Oznacza to, że wszystkie warunki zmienią znak na przeciwny.
- W ten sam sposób zaleca się pozbycie się frakcji. Po prostu pomnóż równanie przez odpowiedni mnożnik, aby zmniejszyć mianowniki.

Przykłady
Wymagane są następujące równania kwadratowe:
x 2 - 7x = 0;
5x 2 - 30 = 0;
15 - 2x - x 2 = 0;
x 2 + 8 + 3 x = 0;
12x + x 2 + 36 = 0;
(x + 1) 2 + x + 1 = (x + 1) (x + 2).
Pierwsze równanie: x 2 - 7x = 0. Jest ono niekompletne, dlatego zostało rozwiązane jak opisano dla formuły drugiej.
Po odłożeniu nawiasów, x (x - 7) = 0.
Pierwszy root przyjmuje wartość: x 1 = 0. Drugi znajdziemy w równaniu liniowym: x - 7 = 0. Łatwo zauważyć, że x 2 = 7.
Drugie równanie: 5x 2 + 30 = 0. Znowu niekompletne. Jest rozwiązany tylko zgodnie z opisem dla trzeciej formuły.
Po przeniesieniu 30 na prawą stronę równania: 5x 2 = 30. Teraz musisz podzielić przez 5. Okazuje się, że: x 2 = 6. Odpowiedzi będą numerami: x 1 = √6, x 2 = - √6.
Trzecie równanie: 15 - 2x - x 2 = 0. Dalej, rozwiązanie równań kwadratowych rozpocznie się od przepisania ich na standardową postać: - x 2 - 2x + 15 = 0. Teraz czas na drugą użyteczną radę i pomnożenie wszystkiego przez minus jeden . Okazuje się, że x 2 + 2x - 15 = 0. Zgodnie z czwartą formułą, dyskryminator musi być obliczony: D = 2 2 - 4 * (- 15) = 4 + 60 = 64. Jest to liczba dodatnia. Z tego, co zostało powiedziane powyżej, wynika, że równanie ma dwa pierwiastki. Należy je obliczyć za pomocą piątej formuły. Oznacza to, że x = (-2 ± √64) / 2 = (-2 ± 8) / 2. Następnie x 1 = 3, x 2 = - 5.
Czwarte równanie x 2 + 8 + 3x = 0 konwertuje na to: x 2 + 3x + 8 = 0. Jego dyskryminator jest równy tej wartości: -23. Ponieważ liczba ta jest ujemna, odpowiedź na to zadanie będzie następująca: "Nie ma korzeni".
Piąte równanie 12x + x 2 + 36 = 0 powinno zostać przepisane w następujący sposób: x 2 + 12x + 36 = 0. Po zastosowaniu wzoru dla dyskryminatora otrzymujemy liczbę zero. Oznacza to, że będzie miał jeden rdzeń, a mianowicie: x = -12 / (2 * 1) = -6.
Szóste równanie (x + 1) 2 + x + 1 = (x + 1) (x + 2) wymaga transformacji, polegającej na wprowadzeniu takich pojęć przed otwarciem nawiasów. W miejscu pierwszego pojawi się następujące wyrażenie: x 2 + 2x + 1. Po wyrównaniu pojawi się ten rekord: x 2 + 3x + 2. Po zliczeniu takich pojęć, równanie będzie wyglądać następująco: x 2 - x = 0. Zostało zamienione na niekompletne . Podobny do niego został już uznany za nieco wyższy. Korzenie tego będą numerami 0 i 1.